Aufgabe 3.1: Spektrum des Exponentialimpulses

Exponentialimpuls

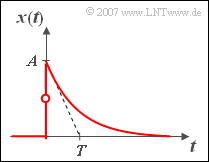
In dieser Aufgabe wird ein kausales Signal $x(t)$ betrachtet,

das zum Zeitpunkt $t = 0$ sprungartig von Null auf $A$ ansteigt, und
für Zeiten $t > 0$ exponentiell mit der Zeitkonstanten $T$ abfällt:

$$x(t) = A \cdot {\rm e}^{ - t/T} .$$

An der Sprungstelle zum Zeitpunkt $t = 0$ gilt $x(t = 0) = A/2$.

Verwenden Sie für die numerischen Berechnungen folgende Parameter:

$$A = 3 \hspace{0.1cm} {\rm V}, \hspace{0.4cm} T = 1 \hspace{0.1cm} {\rm ms} .$$

Die zu berechnende Spektralfunktion $X(f)$ wird komplex sein und kann daher

nach Real– und Imaginärteil, aber auch
nach Betrag und Phase

dargestellt werden. Verwenden Sie hierbei die Notation:

$$X( f ) = \left| {X( f )} \right| \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \varphi( f )} .$$

Hinweis:

Die Aufgabe gehört zum Kapitel Fouriertransformation und –rücktransformation.

Fragebogen

$\text{Re}[X(f=0)] \ = \ $

$\rm mV/Hz$

$\text{Im}[X(f=0)] \ = \ $

$\rm mV/Hz$

$\text{Re}[X(f=f_0)] \ = \ $

$\rm mV/Hz$

$\text{Im}[X(f=f_0)] \ = \ $

$\rm mV/Hz$

$|X(f=f_0)| \hspace{0.25cm} = \ $

$\rm mV/Hz$

$|X(f\rightarrow \infty)| \ = \ $

$\rm mV/Hz$

$\varphi(f=f_0) \hspace{0.25cm} = \ $

$\rm rad$

$\varphi(f \rightarrow \infty) \ = \ $

$\rm rad$

Musterlösung

(1) Mit dem ersten Fourierintegral erhält man:

$$X( f ) = \int_0^\infty {A \cdot {\rm e}^{ - t\left( {1/T + {\rm j \hspace{0.05cm} \cdot \hspace{0.05cm}}2\pi f} \right)} } {\rm d}t = \left. {\frac{ { - A}}{ {1/T + {\rm j}2\pi f}} \cdot {\rm e}^{ - t\left( {1/T + {\rm j}2\pi f} \right)} } \right|_0^\infty .$$

Die obere Integralgrenze $(t \rightarrow \infty)$ ergibt Null, die untere Grenze $(t = 0)$ den Wert $1$. Somit gilt:

$$X(f) = \frac{ {A \cdot T}}{ {1 + {\rm j}2\pi fT}}\hspace{0.3 cm}\Rightarrow\hspace{0.3 cm} X( {f = 0}) = A \cdot T{ = 3 \cdot 10^{ - 3}\; {\rm V/Hz}} \hspace{0.15 cm}\underline{ = 3 \; {\rm mV/Hz}}.$$

Bei der Frequenz $f = 0$ ist demnach das Spektrum rein reell:

$$\text{Re}[X(f=0)] \hspace{0.15 cm}\underline{ = 3 \; {\rm mV/Hz}} \hspace{1.15 cm}\text{Im}[X(f=0)] \hspace{0.15 cm}\underline{ =0}.$$

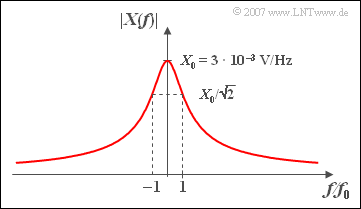
(2) Mit den Abkürzungen $X_0 = A \cdot T$ und $f_0 = 1/(2\pi T)$ lautet die Spektralfunktion:

$$X( f) = \frac{ {X_0 }}{ {1 +{\rm j} \cdot f/f_0 }} = \frac{ {X_0 }}{ {1 + \left( {f/f_0 } \right)^2 }} \cdot \left( {1 - {\rm j} \cdot f/f_0 } \right).$$

Aufgeteilt nach Real- und Imaginärteil ergibt dies:

$${\mathop{\rm Re}\nolimits} [ {X(f)}] = \frac{ {X_0 }}{{1 + \left( {f/f_0 } \right)^2 }}, \hspace{0.5 cm}{\mathop{\rm Im}\nolimits} [ {X(f)}] = - \frac{ {X_0 \cdot f/f_0 }}{ {1 + \left( {f/f_0 } \right)^2 }}.$$

Bei der Frequenz $f_0$ ist

der Realteil gleich $X_0/2 \hspace{0.15 cm}\underline{ = 1.5 \; {\rm mV/Hz}},$
der Imaginärteil gleich $–X_0/2 \hspace{0.15 cm}\underline{ = \hspace{0.1 cm}-1.5 \; {\rm mV/Hz}}.$

(3) Der Betrag einer komplexwertigen Funktion, die als Quotient vorliegt, ist gleich dem Quotienten der Beträge von Zähler und Nenner.

Betragsspektrum des Exponentialimpulses

Damit erhält man:

$$ \left| {X( f)} \right| =\frac{ {X_0 }}{ {\left| 1 +{\rm j} \cdot f/ {f_0 } \right|}} = \frac{ {X_0 }}{{\sqrt {1 + \left( {f/f_0 } \right)^2 } }},$$

$$\Rightarrow \hspace{0.5 cm} \left| {X( {f = f_0} )} \right| = { {X_0 }}/{ {\sqrt 2 }}\hspace{0.15 cm}\underline{ = 2.12 \;{\rm mV/Hz}}.$$

Bei sehr großen Frequenzen $(f \rightarrow \infty)$ ist der Betrag nahezu Null (siehe Skizze).

(4) Für die Phasenfunktion gilt allgemein:

$$\varphi ( f ) = \arctan \left( {\frac{ { - {\mathop{\rm Im}\nolimits}[{X(f)} ]}}{{ {\mathop{\rm Re}\nolimits} [ {X(f)} ]}}} \right) = \arctan \left( {f/f_0 } \right).$$

Für $f = f_0$ ergibt sich $\arctan(1)= \pi /4 \hspace{0.15 cm}\underline{\approx 0.785}$.
Für sehr große Werte von $f$ nähert sich die Phasenfunktion dem Wert $\arctan(\infty) = \pi /2 \hspace{0.15 cm}\underline{ \approx 1.571}$ an.
Beide Angaben sind im Bogenmaß („Radian”) zu verstehen.