Aufgabe 4.5Z: Nochmals Transinformation

• Zurück zum Buch

Gegebene Verbund–WDF und Schaubild der differentiellen Entropien

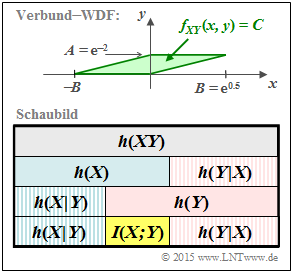
Die Grafik zeigt oben die in dieser Aufgabe zu betrachtende Verbund–WDF  $f_{XY}(x, y)$,  die identisch ist mit der „grünen” Konstellation in der  Aufgabe 4.5.

• $f_{XY}(x, y)$  ist in der  $y$–Richtung um den Faktor  $3$  vergrößert.
• Im grün hinterlegten Definitionsgebiet ist die Verbund–WDF konstant gleich  $C = 1/F$, wobei  $F$  die Fläche des Parallelogramms angibt.

In der Aufgabe 4.5 wurden folgende differentielle Entropien berechnet:

$$h(X) \ = \ {\rm log} \hspace{0.1cm} (\hspace{0.05cm}A\hspace{0.05cm})\hspace{0.05cm},$$

$$h(Y) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}B \cdot \sqrt{ {\rm e } } \hspace{0.05cm})\hspace{0.05cm},$$

$$h(XY) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}F \hspace{0.05cm}) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}A \cdot B \hspace{0.05cm})\hspace{0.05cm}.$$

In dieser Aufgabe sind nun die Parameterwerte  $A = {\rm e}^{-2}$  und  $B = {\rm e}^{0.5}$  zu verwenden.

Entsprechend dem obigen Schaubild sollen nun auch die bedingten differentiellen Entropien  $h(Y|X)$  und  $h(X|Y)$  ermittelt und deren Bezug zur Transinformation  $I(X; Y)$  angegeben werden.

Hinweise:

• Die Aufgabe gehört zum Kapitel  AWGN–Kanalkapazität bei wertkontinuierlichem Eingang.
• Sollen die Ergebnisse in „nat” angegeben werden, so erreicht man dies mit „log”  ⇒  „ln”.
• Sollen die Ergebnisse in „bit” angegeben werden, so erreicht man dies mit „log”  ⇒  „log₂”.

Fragebogen

1

Geben Sie die folgenden informationstheoretischen Größen in „nat” an:

$h(X) \ = \ $ $\ \rm nat$

$h(Y) \ \hspace{0.03cm} = \ $ $\ \rm nat$

$h(XY)\ \hspace{0.17cm} = \ $ $\ \rm nat$

$I(X;Y)\ = \ $ $\ \rm nat$

2

Wie lauten die gleichen Größen mit der Pseudo–Einheit „bit”?

$h(X) \ = \ $ $\ \rm bit$

$h(Y) \ \hspace{0.03cm} = \ $ $\ \rm bit$

$h(XY)\ \hspace{0.17cm} = \ $ $\ \rm bit$

$I(X;Y)\ = \ $ $\ \rm bit$

3

Berechnen Sie die bedingte differentielle Entropie  $h(Y|X)$.

$h(Y|X) \ = \ $ $\ \rm nat$

$h(Y|X) \ = \ $ $\ \rm bit$

4

Berechnen Sie die bedingte differentielle Entropie  $h(X|Y)$.

$h(X|Y) \ = \ $ $\ \rm nat$

$h(X|Y) \ = \ $ $\ \rm bit$

5

Welche der folgenden Größen sind niemals negativ?

	Sowohl  $H(X)$  als auch  $H(Y)$  im wertdiskreten Fall.
	Die Transinformation  $I(X; Y)$  im wertdiskreten Fall.
	Die Transinformation  $I(X; Y)$  im wertkontinuierlichen Fall.
	Sowohl  $h(X)$  als auch  $h(Y)$  im wertkontinuierlichen Fall.
	Sowohl  $h(X|Y)$  als auch  $h(Y|X)$  im wertkontinuierlichen Fall.
	Die Verbundentropie  $h(XY)$  im wertkontinuierlichen Fall.

Musterlösung

Musterlösung

(1)  Da die Ergebnisse in „nat” gefordert sind, bietet sich die Verwendung des natürlichen Logarithmus an:

• Die Zufallsgröße  $X$  ist gleichverteilt zwischen  $0$  und  $1/{\rm e}^2={\rm e}^{-2}$:

$$h(X) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-2}\hspace{0.05cm}) \hspace{0.15cm}\underline{= -2\,{\rm nat}}\hspace{0.05cm}. $$

• Die Zufallsgröße  $Y$  ist dreieckverteilt zwischen  $±{\rm e}^{-0.5}$:

$$h(Y) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}\sqrt{ {\rm e} } \cdot \sqrt{ {\rm e} } ) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{ { \rm e } } \hspace{0.05cm}) \hspace{0.15cm}\underline{= +1\,{\rm nat}}\hspace{0.05cm}.$$

• Die Fläche des Parallelogramms ergibt sich zu

$$F = A \cdot B = {\rm e}^{-2} \cdot {\rm e}^{0.5} = {\rm e}^{-1.5}\hspace{0.05cm}.$$

• Damit hat die 2D–WDF im grün hinterlegten Bereich die konstante Höhe  $C = 1/F ={\rm e}^{1.5}$  und man erhält für die Verbundentropie:

$$h(XY) = {\rm ln} \hspace{0.1cm} (F) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-1.5}\hspace{0.05cm}) \hspace{0.15cm}\underline{= -1.5\,{\rm nat}}\hspace{0.05cm}.$$

• Daraus ergibt sich für die Transinformation:

$$I(X;Y) = h(X) + h(Y) - h(XY) = -2 \,{\rm nat} + 1 \,{\rm nat} - (-1.5 \,{\rm nat} ) \hspace{0.15cm}\underline{= 0.5\,{\rm nat}}\hspace{0.05cm}.$$

(2)  Allgemein gilt der Zusammenhang  $\log_2(x) = \ln(x)/\ln(2)$.  Damit erhält man mit den Ergebnissen der Teilaufgabe  (1):

$$h(X) \ = \ \frac{-2\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.886\,{\rm bit}}\hspace{0.05cm},$$

$$h(Y) \ = \ \frac{+1\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= +1.443\,{\rm bit}}\hspace{0.05cm},$$

$$h(XY) \ = \ \frac{-1.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.164\,{\rm bit}}\hspace{0.05cm},$$

$$I(X;Y) \ = \ \frac{0.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$

• Oder auch:

$$I(X;Y) = -2.886 \,{\rm bit} + 1.443 \,{\rm bit}+ 2.164 \,{\rm bit}{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$

(3)  Die Transinformation kann auch in der Form  $I(X;Y) = h(Y)-h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) $  geschrieben werden:

$$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 1 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= 0.5\,{\rm nat}= 0.721\,{\rm bit}}\hspace{0.05cm}.$$

(4)  Für die differentielle Rückschlussentropie gilt entsprechend:

$$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = -2 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= -2.5\,{\rm nat}= -3.607\,{\rm bit}}\hspace{0.05cm}.$$

Zusammenfassung aller Ergebnisse dieser Aufgabe

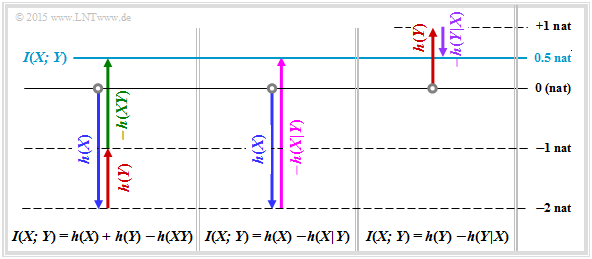
• Alle hier berechneten Größen sind in der Grafik zusammengestellt. 
• Pfeile nach oben kennzeichnen einen positiven Beitrag, Pfeile nach unten einen negativen.

(5)  Richtig sind die Lösungsvorschläge 1 bis 3.

Nochmals zur Verdeutlichung:

• Für die Transinformation gilt stets  $I(X;Y) \ge 0$.
• Im wertdiskreten Fall gibt es keine negative Entropie, jedoch im wertkontinuierlichen.