OFDM für 4G–Netze

1. Modulationsverfahren
2. Vielfachzugriffsverfahren
3. OFDM für 4G–Netze

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Multiplexverfahren vs. Vielfachzugriffsverfahren

Als erstes Beispiel wollen wir nun einen Blick auf die Mobilfunknetze der vierten Generation  $\rm (4G)$  werfen,  die als Nachfolger die früheren Mobilfunknetze,  basierend auf

• $\rm TDMA/FDMA$, siehe  $\rm GSM$  ("Global System for Mobile Communications"),  bzw.
• $\rm CDMA$, siehe  $\rm UMTS$  ("Universal Mobile Telecommunications System")

abgelöst haben.

• Ein weiterer Name,  der häufig synonym zu „4G” verwendet wird,  ist  $\rm LTE$  ("Long Term Evolution").  Ebenso wie  WiMAX  ("Worldwide Interoperability for Microwave Access")  verwendet LTE als Vielfachzugriffsverfahren  $\rm OFDMA$  ("Orthogonal Frequency Division Multiple Access").

• Der wesentliche Unterschied zwischen einem reinen  $\rm Multiplexverfahren$  $($TDM,  FDM,  CDM,  OFDM$)$  und einem  $\rm Vielfachzugriffsverfahren$  $($TDMA,  FDMA,  CDMA,  OFDMA$)$  besteht in der durch Ressourcenzuweisung realisierten Benutzertrennung.  Im Fall von OFDMA bedeutet dies,  dass nicht nur Zeitschlitze  (TDMA)  oder Spreizcodes  (CDMA)  den einzelnen Teilnehmern zugewiesen werden,  sondern verschiedene und „möglichst” orthogonale Unterträger.

• Die Realisierung eines geeigneten Zuteilungsmechanismus’ stellt ein nicht triviales Problem dar,  auf das hier nur sehr oberflächlich eingegangen werden kann.  Sinnvollerweise beschränkt sich ein Verfahren nicht auf eine  (die physikalische)  Schicht,  sondern arbeitet schichtenübergreifend.  Der Begriff „Schicht” ist hier im Sinne des  OSI–Referenzmodells  zu verstehen.

• Notwendig wird dies auch durch die sich verändernden Anforderungen an ein Mobilfunknetz.  Standen zu Anfang der Mobilkommunikation  verbindungsorientierte  Dienste wie Sprachtelefonie im Vordergrund,  stellen heute  paketorientierte  Anwendungen wie  "Voice over IP"  (VoIP),  "Videotelefonie"  oder  "mobile Datendienste"  die hauptsächliche Verkehrslast dar und sind die Ursache für den gestiegenen Anspruch an die zur Verfügung stehenden Datenraten.

Einige Eigenschaften von Mobilfunksystemen

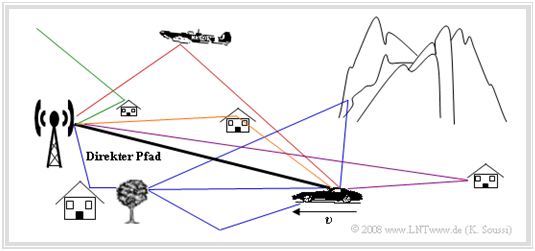
Zuerst soll in aller Kürze auf die Besonderheiten des Mobilfunkkanals eingegangen werden.  Die Abbildung zeigt ein typisches Mobilfunkszenario.  Genauere Informationen zu dieser Thematik finden Sie im Buch  Mobile Kommunikation.

Eigenschaften des Mobilfunkkanals

Wesentliche Eigenschaften des Mobilfunkkanals sind:

• die entfernungsabhängige Dämpfung  ("Path Loss"),
• Brechungs–, Streuungs– und Reflexionseffekte   ⇒   Mehrwegeausbreitung,
• mögliche Abschattungen durch Berge, Bäume und Häuser,
• der Dopplereffekt durch die Relativgeschwindigkeit von Sender und Empfänger.

Bezüglich  „Dämpfung”  unterscheidet man

• zwischen  "zeitabhängiger Dämpfung"  (englisch:  "time-selective fading")
• und  "frequenzabhängiger Dämpfung"  (englisch:  "frequency-selective fading").

Zur Beschreibung von zeitabhängiger und frequenzabhängiger Dämpfung

In nebenstehender Tabelle sind die jeweiligen Beschreibungsgrößen zusammengestellt.  Bitte beachten Sie:   Die Kohärenzbandbreite  $f_{\rm coh}$  ist nicht der Kehrwert der Kohärenzzeit  $T_{\rm coh}$,  obwohl man dies aufgrund vergleichbarer Namensgebung vermuten könnte.

• $f_{\rm coh}$  ist eine Kenngröße für die frequenzabhängige Dämpfung und ergibt sich als der Kehrwert vom  "Delay Spread".
• $T_{\rm coh}$  beschreibt dagegen die zeitabhängige Dämpfung und ist der Kehrwert vom  "Doppler Spread".

Bestimmung einiger OFDM–Parameter

Nun soll versucht werden,  das OFDM–System derart an den Kanal anzupassen,  dass weder zeit– noch frequenzabhängiges Fading auftritt.  Dafür muss gelten:

• Zeitabhängiges Fading wird vermieden  (das heißt:  der Kanal ist zeitinvariant),  wenn die Rahmendauer  ("Time of Interest")  $T_{\rm R} = T + T_{\rm G})$  deutlich kleiner ist als die Kohärenzzeit  $T_{\rm coh}$.
• Frequenzselektives Fading  (innerhalb eines Subträgers)  vermeidet man,  wenn die Bandbreite aller Träger  $(≈ f_0)$  deutlich kleiner ist als die Kohärenzbandbreite  $f_{\rm coh}$:

$$f_0 = {1}/{T} \ll f_{{\rm{coh}}} = {1}/{{T_{\rm{D}} }} \approx {1}/{{T_{\rm{G}} }} \hspace{1.0cm}({\rm z.B.\hspace{0.12cm} f\ddot{u}r }\hspace{0.15cm} \tau_{\rm min}= 0,\hspace{0.12cm}\tau_{\rm max}= T_{\rm G}\hspace{0.12cm}{\rm zutreffend}).$$

• Beide Forderungen lassen sich durch folgende Ungleichung bezüglich der Symboldauer  $T$  zusammenfassen:

$$T_{\rm{G}} \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}.$$

• Beide Forderungen lassen sich aber nicht gleichzeitig erfüllen:   Ein größeres  $T$  veringert zwar die Frequenzselektivität,  macht aber gleichzeitig die Übertragung anfälliger für Doppler–Spreizungen  $($kleineres Verhältnis  $T_{\rm coh}/T)$.

$\text{Beispiel 1:}$  Unter der Annahme einer gegebenen Kohärenzzeit  $T_{\rm coh}$  und der maximalen Verzögerung  $τ_{\rm max}$  durch den Kanal könnte man wie folgt vorgehen:

1. Festlegung des vorläufigen Guard–Intervalls zu  ${T_{\rm G} }' ≥ τ_{\rm max}$,
2. Berechnung der oberen und unteren Grenze:  ${T_{\rm G} }' \ll T \ll T_{\rm coh} – {T_{\rm G} }'$,
3. Berechnung der optimalen Symboldauer als geometrisches Mittel:

$$T_{\rm opt} = \sqrt { {T_{\rm G} }' \cdot (T_{\rm coh} - {T_{\rm G} }') }.$$

• Die notwendige Anzahl  $N_{\rm Nutz}$  an Unterträgern  – und damit auch die minimale FFT–Stützstellenzahl –  ergibt sich daraus zusammen mit der Datenrate  $R$  und der Anzahl  $M$  der Signalraumpunkte des verwendeten Mappings nach Aufrundung:

$$N_{ {\rm{Nutz} } } = \left\lceil {\frac{ {R \cdot (T + {T_{\rm G} }') } } { { {\rm{log}_2}(M)} } } \right\rceil \hspace{0.3cm}\Rightarrow \hspace{0.3cm} N_{ {\rm{FFT} } } = 2^{\left\lceil { {\rm{log}_2} (N_{ {\rm{Nutz} } } )} \right\rceil }.$$

• Der Wert  $N_{\rm FFT}$  berücksichtigt dabei,  dass die Stützstellenzahl der FFT eine Zweierpotenz sein muss.  Die wegen der FFT–Anpassung ungenutzten Träger verwendet man an den Rändern des Spektrums als zusätzliches Schutzband.

• Das resultierende Guard–Intervall muss nun an die neuen Parameter angeglichen werden:

$$T_{\rm{G} } = N_{\rm{G} } \cdot \frac{{T_{{\rm{opt} } } } } { {N_{ {\rm{FFT} } } }} \quad {\rm{mit}} \quad N_{\rm{G} } = \left\lceil {\frac{ { {T_{\rm G} }' } } { {T_{ {\rm{opt} } } } } \cdot N_{ {\rm{FFT} } } } \right\rceil.$$

• Die Rahmendauer ergibt sich zu  $T_{\rm R} = T + T_{\rm G}$  und die Gesamtzahl der Abtastwerte eines Rahmens zu  $N_{\rm gesamt} = N_{\rm FFT} + N_{\rm G}$.  Abschließend muss noch mit obiger Gleichung die Anzahl  $N_{\rm Nutz}$  der Nutzträger erneut berechnet werden.

Ressourcenverwaltung in 4G–Netzen

Ein bisher noch nicht betrachteter Design–Parameter ist die Wahl des jeweiligen Modulationsverfahrens der einzelnen Unterträger,  das entscheidenden Einfluss auf die Fehlerwahrscheinlichkeit bei der Übertragung hat. 

"Multi-User Diversity Gain"  aus  [Vie17].    
Wir bedanken uns bei Ingo Viering für die Erlaubnis, die Grafik verwenden zu dürfen.

Cross-Layer-Scheduler

• Prinzipiell kann man sagen, dass die Robustheit mit steigendem  ${\rm log_2}(M)$  abnimmt, da dadurch der Abstand der möglichen Signalraumpunkte verringert wird.

• Ein großer Symbolumfang  $M$  ist jedoch die Vorraussetzung für die gewünschten hohen Datenraten, was nur in guten Kanalzuständen möglich ist. 
• Die Eigenschaften des Kanals unterscheiden sich dabei für die Teilnehmer oft sehr stark und ändern sich über der Zeit.

Ziel eines geeigneten  Scheduling–Verfahrens  ist es nun,

• möglichst nur bei gutem Kanal zu senden und
• in den Dämpfungseinbrüchen andere Teilnehmer zu bedienen.

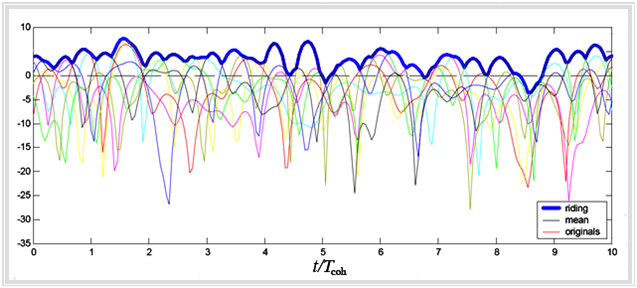
Den damit erzielbaren Gewinn an Systemdurchsatz bezeichnet man oft als  "Multi–User Diversity Gain". 

Die obere Grafik zeigt das Vorgehen.  Die blaue Linie stellt das gewünschte  "Riding on the Peaks"'  für den Fall von acht Teilnehmern  (acht Fading–Prozesse)  dar.

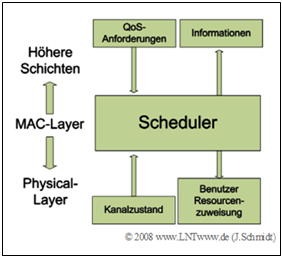
Bei der Realisierung eines kanaladaptiven Schedulers sollten aber auch Informationen aus höheren Schichten mit einbezogen werden,  da je nach  "Quality of Service"  $\rm (QoS$–Anforderung$)$  und Verkehrsart lange Wartezeiten  (große Verzögerungen)  vermieden werden müssen.  In der rechten Grafik ist ein solcher schichtenübergreifender Ansatz  ("Cross–Layer Approach")  schematisch dargestellt.

• Der Scheduler ist dabei im MAC–Layer  ("Medium Access Control Layer")  angesiedelt und kommuniziert mit den anderen  (nicht notwendigerweise benachbarten)  Schichten.  Es sei angemerkt,  dass diese Vorgehensweise dem im OSI–Modell vorgesehenen Modularitätsprinzip widerspricht.
• Ein ähnlicher Ansatz wurde bereits im Rahmen der Erweiterung des UMTS–Netzes um den Standard  $\rm HSDPA$  ("High Speed Downlink Packet Access")  umgesetzt,  wodurch die maximale Datenrate im 3G–Netz (Downstream) von  $\text{384 kbit/s}$  auf theoretisch  $\text{ 14.4 Mbit/s}$  gesteigert werden konnte.

Dieser Abschnitt sollte nur einen groben Ausblick über mögliche zukünftige Mobilfunknetze darstellen.  Festzuhalten bleibt, dass gerade die für sehr hohe Datenraten benötigte verbesserte Adaptivität erst durch den Einsatz eines Mehrträgersystems wie OFDM/OFDMA ermöglicht wird.

Aufgabe zum Kapitel

Aufgabe 5.9:   Wahl der OFDM–Parameter