Aufgabe 3.8Z: Kreis(ring)fläche
Wir betrachten unterschiedlich große Kreise:
- Der Radius $r$ und die Fläche $A$ lassen sich als voneinander abhängige Zufallsgrößen auffassen.
- Es wird vorausgesetzt, dass der Radius auf den Bereich $6 \le r \le 8$ beschränkt ist.
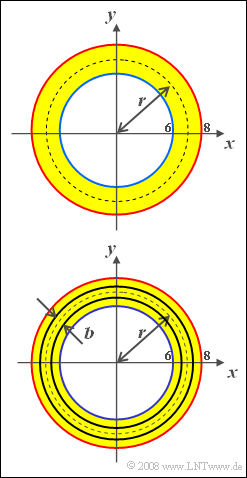
In der oberen Skizze ist der Bereich, in dem solche Kreise $($alle mit Mittelpunkt im Koordinatenursprung$)$ liegen können, gelb markiert. Weiterhin kann davon ausgegangen werden, dass der Radius in diesem Intervall gleichverteilt ist:
- $$f_r(r)=\left\{ \begin{array}{*{4}{c}} 0.5 & \rm f\ddot{u}r\hspace{0.2cm}{\rm 6\le \it r \le \rm 8}, \\\rm 0 & \rm sonst. \end{array} \right.$$
Ab der Teilaufgabe (5) werden schmale Kreisringe mit dem Mittenradius $r$ und der Breite $b$ betrachtet $($untere Skizze$)$:
- Die Fläche eines solchen Kreisrings wird mit $R$ bezeichnet.
- Die möglichen Mittenradien $r$ seien auch hier gleichverteilt zwischen $6$ und $8$.
- Die Kreisringbreite beträgt $b = 0.1$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Exponentialverteilte Zufallsgrößen.
- Insbesondere wird Bezug genommen auf die Seite Transformation von Zufallsgrößen.
Fragebogen
Musterlösung
- Daraus ergibt sich mit $r = 6$ für den Minimalwert:
- $$A_\text{min} \hspace{0.15cm}\underline {= 113.09}.$$
(2) Entsprechend gilt mit $r = 8$ für den Maximalwert:
- $$A_\text{max} \hspace{0.15cm}\underline {= 201.06}.$$
(3) Am einfachsten löst man diese Aufgabe wie folgt:
- $$m_{\rm A}={\rm E}\big[A\big]={\rm E}\big[g(r)\big]=\int_{ -\infty}^{+\infty}g(r)\cdot f_r(r) {\rm d}r.$$
- Mit $g(r) = \pi \cdot r^2$ und $f_r(r) = 1/2$ im Bereich von $6$ ... $8$ erhält man:
- $$m_{\rm A}=\int_{\rm 6}^{\rm 8}1/2 \cdot\pi\cdot r^{\rm 2}\, {\rm d} \it r=\frac{\pi}{\rm 6}\cdot \rm ( 8^3-6^3) \hspace{0.15cm}\underline{=\rm 154.98}.$$
(4) Die WDF der transformierten Zufallsgröße $A$ lautet:
- $$f_A(A)=\frac{f_r(r)}{|g\hspace{0.05cm}'(r)|}\Bigg|_{r=h(y) = \sqrt{A/ \pi }}.$$
- Im Bereich zwischen $A_\text{min} {= 113.09}$ und $A_\text{max} {= 201.06}$ gilt dann:
- $$f_A(A)=\frac{\rm 1/2}{\rm 2\cdot \pi\cdot\it r}\Bigg|_{\it r=\sqrt{\it A/\rm \pi}}=\frac{\rm 1}{\rm 4\cdot\sqrt{\it A\cdot\rm \pi}}.$$
- Die gesuchte Wahrscheinlichkeit erhält man durch Integration:
- $${\rm Pr}(A> 150)=\int_{\rm 150}^{\it A_{\rm max}}\frac{\rm 1}{\rm 4\cdot\sqrt{\it A\cdot\rm \pi}} \; \rm d \it A= \frac{\rm 2\cdot\sqrt{\it A}}{\rm 4\cdot\sqrt{\pi}}\Big|_{\rm 150}^{\it A_{\rm max}}.$$
- Die obere Integrationsgrenze liefert den Wert $4$ und die untere Grenze $3.455$. Daraus ergibt sich die gesuchte Wahrscheinlichkeit:
- $${\rm Pr}(A> 150) \hspace{0.15cm}\underline {=54.5\%}.$$
(5) Für die Kreisringfläche $R$ gilt bei gegebenem Radius $r$:
- $$R=\left (r+{b}/{\rm 2} \right)^{\rm 2}\cdot \rm\pi-\left ({\it r}-{\it b}/{\rm 2} \right)^{\rm 2}\cdot \rm\pi= \rm2\cdot\pi\cdot\it r \cdot b.$$
- Zwischen $R$ und $r$ besteht also ein linearer Zusammenhang.
- Das heißt: $R$ ist ebenfalls gleichverteilt und zwar unabhängig von der Breite $b$, solange $b \ll r$ ist.
- Für den Minimalwert gilt:
- $$R_{\rm min}=\rm 2\pi\cdot 6\cdot 0.1\hspace{0.15cm}\underline{\approx3.77}. $$
(6) Entsprechend ist der Maximalwert:
- $$R_{\rm max}=\rm 2\pi\cdot 8\cdot 0.1\hspace{0.15cm}\underline{\approx 5.03}.$$
(7) Aufgrund des linearen Zusammenhangs zwischen $R$ und $r$ führt der mittlere Radius $r = 7$ auch zur mittleren Kreisringfläche:
- $${\rm E}\big[R\big]=\rm 2\pi\cdot 7\cdot 0.1\hspace{0.15cm}\underline{\approx 4.4}.$$