Aufgabe 5.5: Fast-Fouriertransformation
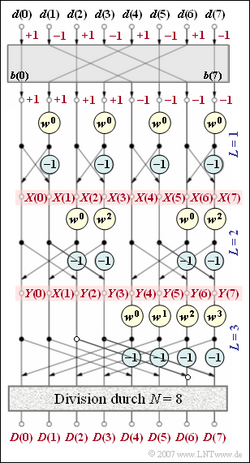
Die Grafik zeigt den Signalflussplan der DFT für $N$ = 8. Aus den Zeitkoeffizienten $d$(0), ... , $d$(7) werden die dazugehörigen Spektralkoeffizienten $D$(0), ... , $D$(7) ermittelt. Für diese gilt mit 0 ≤ μ ≤ 7:
$$D(\mu) = \frac{1}{N}\cdot \sum_{\nu = 0 }^{N-1} d(\nu) \cdot {w}^{\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu}\hspace{0.05cm},$$
wobei der komplexe Drehfaktor $w = \text{exp}(–\text{j}2\pi /N)$ zu verwenden ist, also $\text{exp}(–\text{j}\pi /4)$ für $N$ = 8. Am Eingang wird die alternierende ±1–Folge 〈 $d(ν)$ 〉 angelegt. Nach der Bitumkehroperation ergibt sich daraus die Folge 〈 $b(κ)$ 〉. Es gilt $b(κ) = d(ν)$, wenn man $ν$ als Dualzahl darstellt und die resultierenden 3 Bit als $κ$ in umgekehrter Reihenfolge geschrieben werden. Beispielsweise
- folgt aus $ν$ = 1 (binär 001) die Position $κ$ = 4 (binär 100),
- verbleibt $d$(2) an der gleichen Position 2 (binär 010).
Der eigentliche FFT–Algorithmus geschieht für das Beispiel $N$ = 8 in log2 $N$ = 3 Stufen, die mit L = 1, 2 und 3 bezeichnet werden. Weiter gilt:
- In jeder Stufe sind vier Basisoperationen – sog. Butterflies – durchzuführen sind.
- Die Werte am Ausgang der ersten Stufe werden in dieser Aufgabe mit $X$(0), ... , $X$(7) bezeichnet, die der zweiten mit $Y$(0), ... , $Y$(7).
- Nach der dritten und letzten Stufe sind alle Werte noch durch $N$ zu dividieren.
Hinweis: Die Aufgabe bezieht sich auf den Theorieteil zu Kapitel 5.5.
Fragebogen
Musterlösung
$$8 \cdot D(3) & = & w^0 - w^3 + w^6- w^9+ w^{12}- w^{15}+ w^{18}- w^{21}= \\ & = & w^0 - w^3 + w^2- w^1+ w^{4}- w^{7}+ w^{6}- w^{5}\hspace{0.05cm}.$$
Hierbei ist berücksichtigt, dass aufgrund der Periodizität w9 = w1, w12 = w4, w15 = w7, w18 = w2 und w21 = w5 ist. Nach Umsortieren gilt in gleicher Weise
$$8 \cdot D(3) & = & (w^0 + w^4) - (w^1 + w^5)+ (w^2 + w^6) - (w^3 + w^7) = \\ & = & (1 + w + w^2+ w^3) \cdot (w^0 + w^4)\hspace{0.05cm}.$$
Wegen w0 = 1 und w4 = exp(–j · π) = –1 erhält man somit D(3) = 0. b) In analoger Weise zu a) ergibt sich nun:
$$8 \cdot D(4) & = & w^0 - w^4 + w^8- w^{12}+ w^{16}- w^{20}+ w^{24}- w^{28}= \\ & = & 4 \cdot (w^0 - w^4)= 8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{D(4) = 1}\hspace{0.05cm}.$$
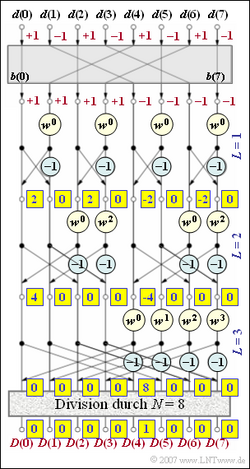
c) Der Term w0 = 1 muss nicht berücksichtigt werden. Alle Ausgangswerte mit ungeraden Indizes sind somit durch die Subtraktion zweier identischer Eingangswerte gleich 0. Die erste Aussage trifft dagegen nicht zu: Es gilt X(0) = X(2) = +2 und X(4) = X(6) = –2 ⇒ Lösungsvorschlag 2.
d) Auf die Multiplikation mit w2 = –j kann verzichtet werden, da im Signalflussplan die entsprechenden Eingangsgrößen 0 sind.
Man erhält somit Y(0) = 4 und Y(4) = –4. Alle anderen Werte sind 0.
e) Wegen Y(5) = Y(6) =Y(7) = 0 spielen auch in der dritten Stufe die Multiplikationen mit w, w2 und w3 keine Rolle. Alle Spektralkoeffizienten D(μ) ergeben sich zu 0 mit Ausnahme von
$$\hspace{0.15 cm}\underline{D(4)} = {1}/{N}\cdot \left[Y(0) - Y(4) \right ] \hspace{0.15 cm}\underline{= 1} \hspace{0.05cm}.$$
Dieses Ergebnis stimmt mit den Ergebnissen aus a) und b) überein.
f) Nachdem sowohl die Zeitkoeffizienten d(ν) als auch alle Spektralkoeffizienten D(μ) rein reell sind, besteht kein Unterschied zwischen der FFT und der IFFT. Das bedeutet gleichzeitig: die Eingangs– und Ausgangswerte können vertauscht werden. Die Teilaufgabe e) hat das folgende Ergebnis geliefert:
$$d({\rm gerades}\hspace{0.15cm}\nu) = +1, \hspace{0.2cm}d({\rm ungerades}\hspace{0.15cm}\nu)= -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D(\mu = 4)= 1,\hspace{0.2cm}D(\mu \ne 4)= 0.$$
Durch Vertauschen der Eingangs– und Ausgangswerte kommt man zur Aufgabenstellung von (f):
$$d(\nu = 4)= 1, \hspace{0.2cm}d(\nu \ne 4)= 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D({\rm gerades}\hspace{0.15cm}\mu) = +1, \hspace{0.2cm}D({\rm ungerades}\hspace{0.15cm}\mu)= -1 \hspace{0.05cm}.$$
Insbesondere würde sich D(3) = –1 und D(4) = +1 ergeben.