Synchrondemodulation

1. Modulationsverfahren
2. Amplitudenmodulation und AM–Demodulation
3. Synchrondemodulation

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Blockschaltbild und Zeitbereichsdarstellung

Eine Modulation am Sender macht nur Sinn, wenn es möglich ist, diese Signalumsetzung am Empfänger wieder rückgängig zu machen und zwar möglichst ohne Informationsverlust.

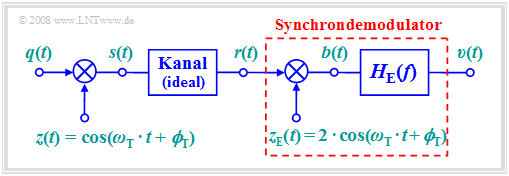
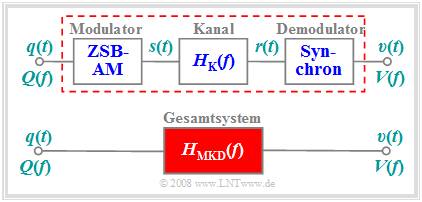
Bei jeder Form von Amplitudenmodulation (sei es ZSB oder ESB, mit oder ohne Träger) erfüllt der so genannte Synchrondemodulator diese Aufgabe. Zu obigem Blockschaltbild ist Folgendes anzumerken:

• Zur Modulation wird beispielhaft ZSB–AM ohne Träger (Modulationsgrad $m → ∞$) betrachtet. Synchrondemodulation ist aber auch anwendbar, wenn der Träger in $s(t)$ enthalten ist.
• Der Kanal sei ideal und die Störungen vernachlässigbar, so dass das Empfangssignal $r(t)$ identisch mit dem Sendesignal $s(t)$ ist:

$$r(t) = s(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \phi_{\rm T})\hspace{0.05cm}.$$

• Im Empfänger wird dieses Signal zunächst mit dem empfängerseitigen Trägersignal

$$z_{\rm E}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t + \phi_{\rm T})$$

multipliziert, das bis auf den Faktor 2 identisch mit dem sendeseitigen Träger $z(t)$ ist.

• Das Ergebnis der Multiplikation ist das Signal

$$\begin{align*}b(t) & = r(t) \cdot z_{\rm E}(t) = 2 \cdot q(t) \cdot \cos^2(\omega_{\rm T} \cdot t + \phi_{\rm T})= \\ & = q(t) + q(t) \cdot \cos(2 \cdot \omega_{\rm T} \cdot t + 2\cdot \phi_{\rm T})\hspace{0.05cm}.\end{align*}$$

Hierbei ist die trigonometrische Umformung $\cos²(α) = 1/2 · (1 + \cos(2α))$ berücksichtigt.

• Der zweite Term liegt im Bereich um die doppelte Trägerfrequenz. Ist $f_{\rm T} > B_{\rm NF}$, was in der Praxis stets zutrifft, so kann dieser Anteil durch einen geeignet dimensionierten Tiefpass $H_{\rm E}(f)$ unterdrückt werden, und man erhält $υ(t) = q(t)$.

Beschreibung im Frequenzbereich

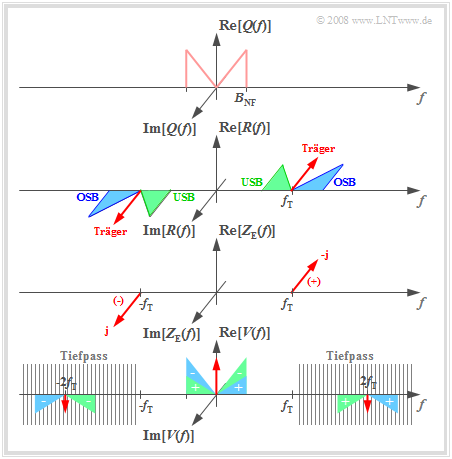
Ausgehend von einem geraden Quellensignal $q(t)$ ⇒ reelles Spektrum $Q(f)$ und einem Sinus–Träger $z(t)$ ergibt sich das imaginäre Sendespektrum $S(f)$ gemäß der zweiten Skizze, wobei mit $A_{\rm T}$ ≠ 0 auch die ZSB–AM mit Träger (rote Diracfunktion) berücksichtigt ist. Aufgrund des idealen Kanals gilt $R(f) = S(f)$.

Die Wirkungsweise des Synchrondemodulators kann im Frequenzbereich wie folgt erklärt werden:

• Das empfängerseitige Trägersignal $z_{\rm E}(t) = 2 · z(t) = 2 · \sin(ω_{\rm T} · t)$ führt im Spektralbereich zu zwei Diracfunktionen bei $\pm f_{\rm T}$ mit den Gewichten ±j. Der negative Imaginärteil tritt bei $f = +f_{\rm T}$ auf.
• Der Multiplikation $b(t) = r(t) · z_{\rm E}(t)$ entspricht die Faltung der zugehörigen Spektralfunktionen:

$$B(f) = R(f) \star Z_{\rm E}(f)\hspace{0.05cm}.$$

• Die Faltung der Diracfunktion –j · $δ(f – f_{\rm T})$ mit dem rein imaginären Spektrum $R(f)$ führt zu rein reellen Spektralanteilen um $f =$ 0 und $f = 2f_{\rm T}$. Diese Anteile sind oben mit einem „+” versehen.
• Das zweite Faltungsprodukt j · $δ(f + f_{\rm T}) \star R(f)$ liefert neben einem Anteil bei $–2f_{\rm T}$ auch einen niederfrequenten Spektralanteil um $f =$ 0. Diese Spektralanteile sind mit „–” markiert.
• Das Spektrum nach dem Tiefpass $H_{\rm E}(f)$ ist $V(f) = Q(f) + A_{\rm T} · δ(f)$. Bei ZSB–AM mit Träger kann durch eine untere Bandbegrenzung, also $H_{\rm E}(f = 0) =$ 0, der störende Gleichanteil entfernt werden.
• Die farbliche Zuordnung in der Grafik (OSB blau, USB grün, Träger rot) lässt erkennen, dass der Synchrondemodulator sowohl das OSB als auch das USB zur Signalrekonstruktion nutzt.

Voraussetzungen für die Anwendung des Synchrondemodulators

Das Ausgangssignal $υ(t)$ ist identisch mit dem Quellensignal $q(t)$, wenn folgende Kriterien erfüllt sind:

• Die Bandbreite $B_{\rm NF}$ des Quellensignals ist kleiner als die Trägerfrequenz $f_{\rm T}$. Diese Einschränkung ist nicht sonderlich gravierend und für die Praxis nicht relevant.

• Die Trägerfrequenzen von Sender und Empfänger stimmen exakt überein. Dies erfordert eine Trägerrückgewinnung beim Empfänger und ist mit gewissen „Kosten” verbunden.

• Zwischen den sende– und empfängerseitig zugesetzten Trägersignalen $z(t)$ und $z_{\rm E}(t)$ besteht zudem eine vollkommene Phasensynchronität.

• Der Kanalfrequenzgang $H_{\rm K}(f)$ ist im Durchlassbereich $f_{\rm T} – B_{\rm NF} ≤ |f| ≤ f_{\rm T} + B_{\rm NF}$ ideal gleich 1. Eine frequenzunabhängige Dämpfung oder frequenzlineare Phase (Laufzeit) werden meist toleriert.

• Der Einfluss des Rauschens und externer Störungen ist vernachlässigbar klein. Aber auch bei nicht vernachlässigbarem Rauschen ist der Synchrondemodulator anderen Demodulatoren überlegen.

• Das Empfangsfilter $H_{\rm E}(f)$ ist für $|f| ≤ B_{\rm NF}$ gleich 1 und für $|f| ≥ 2f_{\rm T} – B_{\rm NF}$ identisch 0. Der Verlauf dazwischen ist nicht relevant (siehe Grafik auf der vorherigen Seite).

• Beim Modulationsverfahren „ZSB–AM mit Träger” muss zusätzlich mit $H_{\rm E}(f = 0) ≡$ 0 sicher gestellt werden, dass der beim Sender zugesetzte Träger im Sinkensignal nicht mehr enthalten ist.

In den nächsten Abschnitten werden die Auswirkungen beschrieben, wenn die in den Punkten 2 bis 5 genannten Voraussetzungen nicht erfüllt sind.

Einfluss eines Frequenzversatzes

Wie der Name „Synchrondemodulator” bereits zum Ausdruck bringt, funktioniert dieser nur bei völliger Synchronität zwischen den Trägersignalen von Sender und Empfänger. Unterscheiden sich dagegen die Trägerfrequenzen um einen Frequenzversatz $Δf_{\rm T}$, zum Beispiel $$\begin{align*}z(t) & = 1 \cdot \cos(2 \pi f_{\rm T} \cdot t + \phi_{\rm T})\hspace{0.05cm}, \\ z_{\rm E}(t) & = 2 \cdot \cos(2 \pi (f_{\rm T} + \Delta f_{\rm T}) \cdot t + \phi_{\rm T})\hspace{0.05cm},\end{align*}$$ so erhält man für das Spektrum des Sinkensignals: $$\begin{align*}V(f) & = \frac{1}{2}\cdot Q(f + \Delta f_{\rm T}) + \frac{1}{2}\cdot Q(f - \Delta f_{\rm T}) = \\ & = Q(f) \star \left[ \frac{1}{2}\cdot \delta(f + \Delta f_{\rm T}) + \frac{1}{2}\cdot \delta (f - \Delta f_{\rm T}) \right] \hspace{0.05cm}.\end{align*}$$

Dieses Ergebnis lässt sich anhand der Skizze auf der Seite Beschreibung im Frequenzbereich leicht verifizieren. Transformiert man obige Gleichung in den Zeitbereich, so erhält man: $$v(t) = q(t) \cdot \cos(2 \pi \cdot \Delta f_{\rm T} \cdot t )\hspace{0.05cm}.$$

Der Frequenzversatz $Δf_{\rm T}$, der auf Realisierungsungenauigkeiten der Trägerrückgewinnung zurückgeht, ist – bezogen auf die Trägerfrequenz – meist sehr klein und bewegt sich im Bereich von einigen Hertz bis etwa 100 Hz. In diesem Zusammenhang spricht man dann von einer Schwebung.

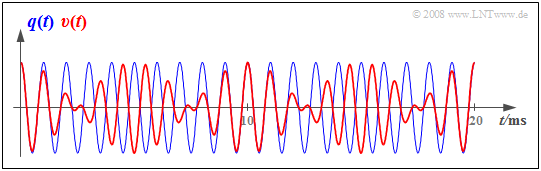
Die Grafik zeigt ein cosinusförmiges Quellensignal mit der Frequenz $f_{\rm N} =$ 1 kHz ⇒ blaue Schwingung und das mit einem Synchrondemodulator gewonnene Sinkensignal $υ(t)$ ⇒ rote Kurve, wobei ein Frequenzversatz von $Δf_{\rm T} =$ 100 Hz zugrundegelegt wurde. Damit ergibt sich: $$\begin{align*}v(t ) & = 1\,{\rm V} \cdot \cos (2 \pi \cdot 1\,{\rm kHz} \cdot t) \cdot \cos (2 \pi \cdot 0.1\,{\rm kHz} \cdot t) \hspace{0.05cm}, \\ & = 0.5\,{\rm V} \cdot \cos (2 \pi \cdot 0.9\,{\rm kHz} \cdot t) + 0.5\,{\rm V} \cdot \cos (2 \pi \cdot 1.1\,{\rm kHz} \cdot t) \hspace{0.05cm}.\end{align*}$$

Spektral gesehen werden aus der 1 kHz–Schwingung zwei Schwingungen mit den Frequenzen 0.9 kHz und 1.1 kHz halber Amplitude. Es entstehen neue Frequenzen – also nichtlineare Verzerrungen. Die gesendete Frequenz (1 kHz) ist dagegen in $υ(t)$ nicht mehr enthalten.

Einfluss eines Phasenversatzes

Nun gelte für das sende– und für das empfängerseitige Trägersignal: $$\begin{align*}z(t) & = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}, \\ z_{\rm E}(t) & = 2 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm E})\hspace{0.05cm}.\end{align*}$$ Damit erhält man für das Signal direkt nach der Multiplikation mit dem Phasenversatz $Δϕ_{\rm T} = ϕ_{\rm E} – ϕ_{\rm T}$: $$\begin{align*}b(t) & = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \phi_{\rm T}) \cdot 2 \cdot \cos(\omega_{\rm T} \cdot t + \phi_{\rm E})= \\ & = q(t)\cdot \cos(\Delta \phi_{\rm T}) + q(t) \cdot \cos(2 \cdot \omega_{\rm T} \cdot t + \phi_{\rm E}+ \phi_{\rm T})\hspace{0.05cm}.\end{align*}$$ Unter Berücksichtigung des Tiefpassfilters ergibt sich somit für das Sinkensignal: $$v(t) = q(t)\cdot \cos(\Delta \phi_{\rm T}) \hspace{0.05cm}.$$

Das bedeutet: Bei ZSB–AM (mit oder ohne Träger) führt die Synchrondemodulation mit Phasenversatz nicht zu Verzerrungen, sondern lediglich zu einer frequenzunabhängigen Dämpfung um $\cos(Δϕ_{\rm }T)$. Der Grund für diese weniger gravierende Signalveränderung ist, dass hier im Gegensatz zur Gleichung für den Frequenzversatz die Zeit im Argument der Cosinusfunktion fehlt.

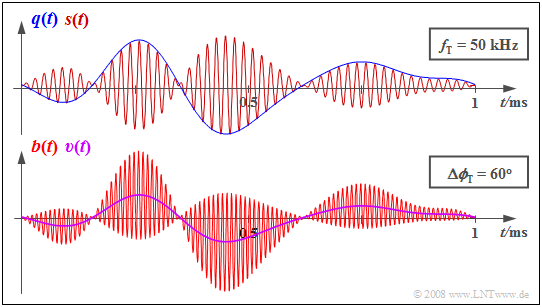
Die nachfolgende Grafik zeigt oben die Signale $q(t)$ und $s(t)$ am Sender und unten die empfängerseitigen Signale $b(t)$ und $υ(t)$.

Aufgrund des Phasenversatzes um $Δϕ_{\rm T} =$ π/3 (60°) ist das Sinkensignal $υ(t)$ nur halb so groß wie das Quellensignal $q(t)$. Die Signalform bleibt jedoch erhalten.

Einfluss linearer Kanalverzerrungen (1)

Im Kapitel 2.3 von Buch „Lineare zeitinvariante Systeme” wurde bereits angedeutet, dass das gesamte Übertragungssystem – bestehend aus Modulator, Kanal und Demodulator – durch den resultierenden Frequenzgang $H_{\rm MKD}(f)$ vollständig beschrieben werden kann, wenn

• das System entweder verzerrungsfrei ist, oder
• lediglich lineare Verzerrungen hinsichtlich der Signale $q(t)$ und $υ(t)$ entstehen.

Nichtlineare Verzerrungen werden durch dieses Ersatzschaltbild nicht erfasst, da aufgrund der Gleichung $$V(f) = Q(f)\cdot H_{\rm MKD}(f)$$ das Entstehen neuer Frequenzen nicht möglich ist. Ist $Q(f_0) =$ 0, so wird stets auch $V(f_0) =$ 0 gelten.

Die obigen Voraussetzungen sind bei folgender Systemvariante erfüllt:

• Der Modulator erzeugt eine ZSB–AM (mit oder ohne Träger) um die Trägerfrequenz $f_{\rm T}$.
• Der Kanal ist durch den Frequenzgang $H_{\rm K}(f)$ mit Bandpass–Charakter beschreibbar.
• Der Synchrondemodulator ist frequenz– und phasensynchron und das Filter $H_{\rm E}(f)$ rechteckförmig.

Einfluss linearer Kanalverzerrungen (2)

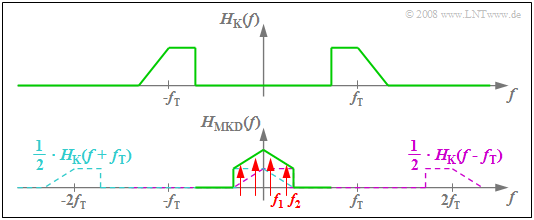
Damit lautet der resultierende Frequenzgang von Modulator–Kanal–Demodulator: $$H_{\rm MKD}(f) = \frac{1}{2} \cdot \left[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\right] \hspace{0.05cm}.$$

Ist der Gesamtfrequenzgang $H_{\rm MKD}(f)$ nicht konstant, so werden die verschiedenen Spektralanteile des Quellensignals $q(t)$ auch unterschiedlich übertragen. Ebenso kann es zu Phasenverzerrungen kommen, wenn die Phasenfunktion nichtlinear in $f$ ist.

Die Grafik verdeutlicht die obige Berechnungsvorschrift für die resultierende Systemfunktion. Aus dem unsymmetrischen Bandpass $H_{\rm K}(f)$ – bezogen auf die Trägerfrequenz $f_{\rm T}$ – wird die im NF–Bereich (um $f =$ 0) symmetrische Funktion $H_{\rm MKD}(f)$.

Besteht das Quellensignal aus zwei Frequenzanteilen – in der Grafik an den roten Markierungspfeilen zu erkennen – so wird die Spektrallinie bei $f_2$ stärker gedämpft als die Frequenz $f_1$. Es gibt lineare Dämpfungsverzerrungen. Dass $H_{\rm MKD}(f)$ auch Anteile um $±2f_{\rm T}$ beinhaltet, ist nicht weiter störend.

Einfluss von Rauschstörungen (1)

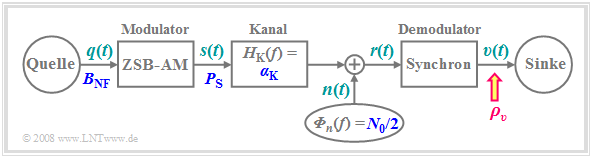
Nun soll die Frage geklärt werden, in wie weit die Übertragungsqualität durch ein stochastisches Stör- bzw. Rauschsignal $n(t)$ beeinträchtigt wird. Wir gehen dabei von folgendem Szenario aus, das bereits auf der Seite Untersuchungen beim AWGN–Kanal in Kapitel 1.2 vorgestellt wurde.

Insbesondere werden folgende Annahmen getroffen:

• Betrachtet wird eine Zweiseitenband–Amplitudenmodulation mit dem Modulationsgrad $m$ sowie ein idealer Synchrondemodulator ohne Phasen- und Frequenzversatz.
• Entsprechend dem erweiterten AWGN–Kanalmodell gilt für das Empfangssignal

$$r(t) = \alpha_{\rm K} \cdot s(t) + n(t) \hspace{0.05cm},$$

wobei $α_{\rm K}$ ein frequenzunabhängiger Dämpfungsfaktor ist und das Störsignal $n(t)$ weißes Rauschen mit der zweiseitigen Rauschleistungsdichte $N_0/2$ modelliert.

• Stellvertretend für ein Quellensignal $q(t)$ der Bandbreite $B_{\rm NF}$ wird hier von einem cosinusförmigen Nachrichtensignal ausgegangen:

$$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot B_{\rm NF} \cdot t ) \hspace{0.05cm}.$$

Mit diesen Annahmen gilt für das Sinkensignal $$v(t) = \alpha_{\rm K} \cdot q(t) + \varepsilon(t) \hspace{0.05cm},$$

wobei die Ursache der stochastischen Komponente $ε(t)$ das Bandpass–Rauschen $n(t)$ am Eingang des Synchrondemodulators ist.

Als quantitatives Maß für die Übertragungsqualität wird das Signal–zu–Rausch–Leistungsverhältnis an der Sinke verwendet, das hier mit den Leistungen von $q(t)$ und $ε(t)$ wie folgt lautet: $$\rho_v = \frac{\alpha_{\rm K}^2 \cdot P_q}{P_\varepsilon} \hspace{0.05cm}.$$

Dieses Verhältnis bezeichnen wir im Folgenden kurz als das Sinken–SNR $ρ_υ$ und die logarithmische Darstellung 10 · lg $ρ_υ$ als den Sinken-Störabstand in dB.

Im nächsten Abschnitt berechnen wir zunächst die Leistung $P_ε$ des Fehlersignals $ε(t)$, die wir der Einfachheit halber als „Rauschleistung” bezeichnen.

Einfluss von Rauschstörungen (2)

Berechnung der Rauschleistung $P_ε$

Das Fehlersignal $ε(t)$ erhält man aus dem Störsignal $n(t)$ am Eingang durch

• Multiplikation mit $z_{\rm E}(t) = 2 · \cos(ω_{\rm T} · t + ϕ_{\rm T})$ und
• eine anschließende (ideale) Tiefpassfilterung auf den Frequenzbereich $\pm B_{\rm NF}$.

Für das Leistungsdichtespektrum $Φ_ε'(f)$ ohne Berücksichtigung des Tiefpasses gilt mit $Φ_n(f) = N_0/2$: $${\it \Phi}_\varepsilon \hspace{-0.10cm} '(f) = {\it \Phi}_n (f) \star {\it \Phi}_{z {\rm E}}(f) \hspace{0.05cm}.$$

In den Büchern „Signaldarstellung” und „Stochastische Signaltheorie” wurde gezeigt, dass das Spektrum und das Leistungsdichtespektrum eines Cosinussignals $x(t) = A · \cos(2πf_{\rm T}t)$ wie folgt gegeben sind: $$\begin{align*}X(f) & = \frac{A}{2}\cdot \delta(f + f_{\rm T}) + \frac{A}{2}\cdot \delta(f - f_{\rm T}) \hspace{0.05cm}, \\ {\it \Phi}_x (f) & = \frac{A^2}{4}\cdot \delta(f + f_{\rm T}) + \frac{A^2}{4}\cdot \delta(f - f_{\rm T}) \hspace{0.05cm}.\end{align*}$$

Angewandt auf das empfangsseitige Trägersignal $z_{\rm E}(t)$ lautet die zweite Gleichung mit $A =$ 2, und zwar unabhängig von der Phase (da im Leistungsdichtespektrum alle Phasenbeziehungen verloren gehen): $${\it \Phi}_{z {\rm E}}(f)= \delta(f + f_{\rm T}) + \delta(f - f_{\rm T}) \hspace{0.05cm}.$$

Unter Berücksichtigung, dass $Φ_n(f)$ für alle Frequenzen konstant ist ⇒ „Weißes Rauschen” , ergibt sich: $${\it \Phi}_\varepsilon \hspace{-0.10cm} '(f) = {\it \Phi}_n (f + f_{\rm T}) + {\it \Phi}_n (f - f_{\rm T}) = 2 {\it \Phi}_n (f) = N_0 \hspace{0.05cm}.$$

Das LDS nach dem Tiefpassfilter ist für $|f| < B_{\rm NF}$ genau so groß und außerhalb 0: $${\it \Phi}_\varepsilon (f) = \left\{ \begin{array}{c} N_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}}\\ \\ \end{array}\begin{array}{*{20}c} |f|< B_{\rm NF} \hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}. \\ \end{array}$$

Durch Integration erhält man die Leistung $\mathbf{P_ε = 2N_0 · B_{\rm NF} }$. Mit diesem Zwischenergebnis kann somit für das Sinken–SNR geschrieben werden: $$\rho_v = \frac{\alpha_{\rm K}^2 \cdot P_q}{P_\varepsilon} = \frac{\alpha_{\rm K}^2 \cdot P_q}{N_0 \cdot B_{\rm NF}} \hspace{0.05cm}.$$

Im nächsten Abschnitt wird noch der Zusammenhang zwischen der Leistung $P_q$ des Quellensignals und der Sendeleistung $P_{\rm S}$ hergestellt.

Einfluss von Rauschstörungen (3)

Zusammenhang zwischen $P_q$ und $P_{\rm S}$

Wir benötigen noch den Zusammenhang zwischen den Leistungen von

• Quellensignal $q(t)$ ⇒ Leistung $P_q$, und
• Sendesignal $s(t)$ ⇒ Sendeleistung $P_{\rm S}$.

Im Falle der „ZSB–AM mit Träger” gilt dabei mit dem Modulationsgrad $m$: $$P_{\rm S} = { P_q}/{2} \cdot \hspace{0.05cm} \left( 1 + {2}/{m^2}\right)\hspace{0.05cm}.$$

Anzumerken ist, dass diese Gleichung nur dann anwendbar ist, wenn $q(t)$ eine harmonische Schwingung beschreibt. Die „ZSB–AM ohne Träger” ist in der Gleichung als Sonderfall für $m → ∞$ mit enthalten.

Beweis: Ausgegangen wird jeweils von Cosinusschwingungen, also den folgenden Gleichungen: $$q(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t ) \hspace{0.05cm},$$ $$\begin{align*}s(t) & = \left( q(t) + A_{\rm T}\right) \cdot \cos(\omega_{\rm T} \cdot t ) = \\ & = A_{\rm T} \cdot \cos(\omega_{\rm T} \cdot t ) + {A_{\rm N}}/{2}\cdot \cos((\omega_{\rm T}+ \omega_{\rm N}) \cdot t ) + {A_{\rm N}}/{2}\cdot \cos((\omega_{\rm T}- \omega_{\rm N}) \cdot t )\hspace{0.05cm}.\end{align*}$$ Die Leistung des Quellensignals, bezogen auf den Widerstand 1 Ω, beträgt mit der Periodendauer $T_{\rm N}$: $$P_{q} = \frac{1}{T_{\rm N}}\cdot\int_{0}^{ T_{\rm N}} {q^2(t)}\hspace{0.1cm}{\rm d}t = \frac{A_{\rm N}^2}{T_{\rm N}}\cdot\int_{0}^{T_{\rm N}} {\cos^2(2 \pi\frac{t}{T_{\rm N}})}\hspace{0.1cm}{\rm d}t = \frac{A_{\rm N}^2}{2}\hspace{0.05cm}.$$ Entsprechend erhält man für die Leistung des Sendesignals: $$P_{\rm S} = \frac{A_{\rm T}^2}{2} + \frac{(A_{\rm N}/2)^2}{2} + \frac{(A_{\rm N}/2)^2}{2} = \frac{A_{\rm T}^2}{2} + \frac{A_{\rm N}^2}{4} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm S} = {1}/{2} \cdot \left( P_q + A_{\rm T}^2 \right) \hspace{0.05cm}.$$

Diese Gleichung gilt sowohl für ZSB–AM ohne Träger $(A_{\rm T} = 0)$ als auch für ZSB–AM mit Träger. Da $q(t)$ als eine harmonische Schwingung vorausgesetzt wurde, kann mit dem Modulationsgrad $m = A_{\rm N}/A_{\rm T}$ hierfür auch geschrieben werden: $$P_{\rm S} = \frac{A_{\rm N}^2}{4} \cdot \left( 1 + \frac{2A_{\rm T}^2}{A_{\rm N}^2} \right) = P_{q}/2 \cdot \left( 1 +{2}/{m^2} \right)\hspace{0.05cm}.\hspace{5.4cm}{\rm q.e.d.}$$

Mit diesem weiteren Zwischenergebnis kann somit für das Sinken–SNR geschrieben werden: $$\rho_v = \frac{\alpha_{\rm K}^2 \cdot P_q}{P_\varepsilon} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \cdot \frac{1}{1 + {2}/{m^2}} \hspace{0.05cm}.$$ Nachfolgend wird diese Gleichung ausführlich diskutiert.