Allgemeine Beschreibung von OFDM

1. Modulationsverfahren
2. Vielfachzugriffsverfahren
3. Allgemeine Beschreibung von OFDM

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Das Prinzip von OFDM – Systembetrachtung im Zeitbereich (1)

Orthogonal Frequency Division Multiplex (OFDM) ist ein digitales Mehrträger–Modulationsverfahren mit folgenden Eigenschaften:

• Statt eines breitbandigen, stark modulierten Signals werden zur Datenübertragung eine Vielzahl schmalbandiger, zueinander orthogonaler Unterträger verwendet. Dies ermöglicht unter anderem die Anpassung an einen frequenzselektiven Kanal.
• Die Modulation der Unterträger selbst erfolgt bei OFDM üblicherweise durch eine herkömmliche Quadratur–Amplitudenmodulation (QAM) oder durch binäre Phasenmodulation (BPSK), wobei sich die einzelnen Träger hinsichtlich der Modulationsart durchaus unterscheiden können.
• Unterschiede im Modulationsgrad führen dabei zu verschieden hohen Datenraten der Unterträger. Das heißt also, dass ein hochratiges Quellensignal zur Übertragung in mehrere Signale von deutlich niedrigerer Symbolrate aufgespaltet werden muss.

Die Möglichkeit, für verschiedene Teilbänder unterschiedlich robuste Modulationsverfahren einzusetzen, ist einer der großen Vorteile von OFDM. Hierauf wird in den Abschnitten OFDM für 4G–Netze und Digital Subscriber Line (DSL) noch näher eingegangen.

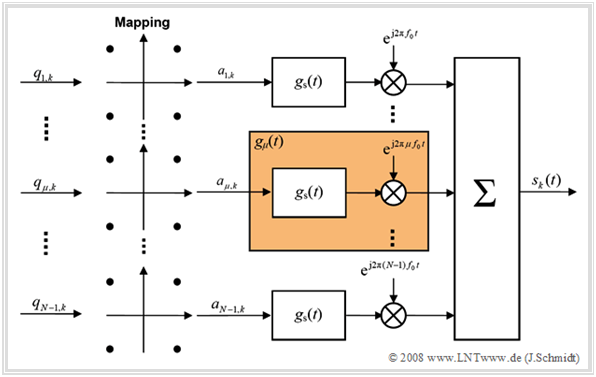
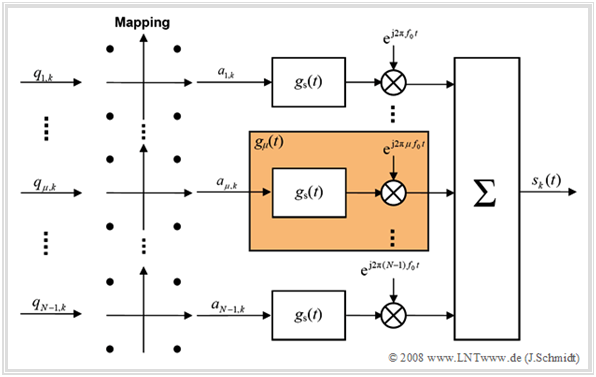
Die Grafik zeigt das Grundprinzip eines OFDM–Senders.

• Die $N$–1 Teile des zur Zeit $k$ anliegenden Datenstroms $〈q_{\mu,k}〉$ werden in diesem durch die Grafik verdeutlichten Beispiel 4–QAM–codiert, indem jeweils zwei Bit zusammengefasst werden.
• Danach wird die im Allgemeinen komplexe Amplitude $a_{\mu,k}$ (mit Laufvariablen $\mu = 1, ... , N–1$) impulsgeformt und mit dem $\mu$–ten Vielfachen der Grundfrequenz $f_0$ moduliert.

Das Prinzip von OFDM – Systembetrachtung im Zeitbereich (2)

Hier nochmals der OFDM–Sender zur Verdeutlichung des dahinter stehenden Prinzips.

Hinweis: In diesem Bild wurde die Darstellung des „nullten” Zweiges $(\mu = 0)$, der den Gleichanteil darstellt, bewusst weggelassen, da dieser häufig zu Null gesetzt wird ⇒ für alle Rahmen $k$ gilt $a_{0, k} =$ 0.

Das Sendesignal ist nun die additive Überlagerung der einzelnen Teilsignale. Die Betrachtung erfolgt hier und auch im Folgenden im äquivalenten Tiefpassbereich, wobei auf den Index „TP” verzichtet wird.

Das Impulsformfilter $g_s(t)$ ist ein auf den Bereich $0 ≤ t < T$ begrenztes Rechteck der Höhe $s_0$. Wir nennen $T$ die Symboldauer und bezeichnen den Kehrwert $f_0 = 1/T$ als die Grundfrequenz.

Fasst man dieses Filter nun mit der jeweiligen Modulation zu $$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm sonst} \\ \end{array} \right.$$ mit $\mu ∈$ {0, ... , $N$–1} zusammen, so ergibt sich das OFDM–Sendesignal $s_k(t)$ im $k$–ten Zeitintervall: $$s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,k} \cdot g_\mu (t - k \cdot T_{\rm{R}} )}.$$ Das gesamte OFDM–Sendesignal unter Berücksichtigung aller Zeitintervalle lautet dann: $$s(t) = \sum\limits_{k = - \infty }^{+\infty} {\sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,k} \cdot g_\mu (t - k \cdot T_{\rm{R}} )} }.$$ $T_{\rm R}$ bezeichnet die Rahmendauer. Innerhalb dieser Zeit liegen die gleichen Daten am Eingang an und nach $T_{\rm R}$ folgt der nächste Rahmen. Für die Symboldauer muss gelten: $T ≤ T_{\rm R}$. Zunächst gelte $T = T_{\rm R}$.

Das Prinzip von OFDM – Systembetrachtung im Zeitbereich (3)

Die Symboldauer $T$ ergibt sich bei einem Mehrträgersystem mit der Anzahl $M$ der Signalraumpunkte und der Bitdauer $T_{\rm B}$ der binären Quellensysmbole allgemein zu $$T = N \cdot {\rm{log}_2}(M) \cdot T_{\rm{B}} ,$$ wobei $N$ wieder die Anzahl der Unterträger angibt.

Wir gehen von einem Einträgersystem mit der Datenrate $R_{\rm B} =$ 768 kbit/s ⇒ $T_{\rm B} ≈$ 1.3 μs und einem Mapping mit $M =$ 4 Signalraumpunkten (4–QAM) aus. Die Symboldauer im Einträgerfall (Single Carrier, SC) beträgt dann: $$T_{{\rm{SC}}} = 1 \cdot {\rm{log}_2}(4) \cdot 1.3 \,{\rm{\mu s}} \approx 2.6 \,{\rm{\mu s}}.$$ Unter der Annahme, dass für ein Mehrträgersystem (Multi Carrier, MC) mit $N =$ 32 Trägern das Modulationsverfahren 16–QAM verwendet wird, ergibt sich dagegen die Symboldauer zu $$T_{{\rm{MC}}} = 32 \cdot {\rm{log}_2}(16) \cdot 1.3 \,{\rm{\mu s}} \approx 0.167 {\rm{ms}}.$$ Die Symboldauer ist in diesem Fall um den Faktor 64 größer.

Fazit: Die Dauer eines Symbols erhöht sich bei einem Mehrträgersystem im Vergleich zu einem Einzelträgersystem deutlich, wodurch der störende Einfluss der Kanalimpulsantwort verringert wird und die Impulsinterferenzen abnehmen.

Systembetrachtung im Frequenzbereich (1)

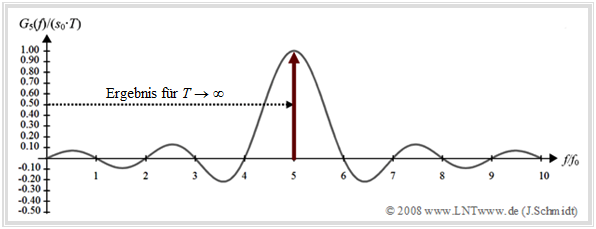
Wir betrachten nochmals das OFDM–Sendesignal im $k$–ten Zeitintervall, wobei wir $T_{\rm R} = T$ setzen: $$s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,k} \cdot g_\mu (t - k \cdot T)}.$$ Den Grundimpuls $g_{\mu}(t)$ nehmen wir vereinfachend symmetrisch um $t =$ 0 an. Dann gilt mit $f_0 = 1/T$: $$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad \quad - T/2 < t < T/2, \\ 0 \quad \quad \quad \quad \quad \quad \; {\rm sonst.} \\ \end{array} \right.$$ Im Spektralbereich korrespondiert eine solche akausale und mit einer (komplexen) Exponentialfunktion der Frequenz $\mu · f_0$ modulierte Rechteckfunktion mit einer um $\mu · f_0$ verschobenen si–Funktion: $$G_\mu (f) = s_0 \cdot T \cdot {\rm{si}} (\pi T (f - \mu f_0 ) ).$$ Die Grafik zeigt diese Spektralfunktion (normiert auf den Maximalwert $s_0 · T$) für $\mu =$ 5.

Der Pfeil soll andeuten, dass im Falle eines zeitlich nicht beschränkten Grundimpulses die dargestellte si–Funktion durch einen Dirac–Impuls an der Stelle $\mu · f_0$ zu ersetzen wäre.

Fazit: Sind alle Amplitudenkoeffizienten $a_{μ,k} ≠ 0$, so setzt sich das Spektrum $S_k(f)$ des Sendesignals im $k$–ten Zeitbereichsintervall aus $N$ um jeweils ein Vielfaches der Grundfrequenz $f_0$ verschobenen si–Funktionen zusammen. Die Funktion ${\rm si}(x) = \sin(x)/x$ wird oft als Spaltfunktion bezeichnet.

Systembetrachtung im Frequenzbereich (2)

Berücksichtigt man weiter, dass wir hier von einem kausalen Grundimpuls $$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0\quad \quad \quad \quad \quad {\rm sonst}, \\ \end{array} \right.$$ ausgehen, so ergibt sich das Spektrum zu $$S_k (f) = s_0 \cdot T \cdot \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,k} \cdot \,} {\rm{si}}(\pi \cdot T(f - \mu \cdot f_0 )) \cdot {\rm{e}}^{ - {\rm{j2\pi}} \frac{T}{2} (f - \mu \cdot f_0 )} .$$ Die komplexe Exponentialfunktion kommt durch die Grenzen des hier zur Impulsformung verwendeten Rechtecks im Zeitbereich (0 ... $T$ ⇒ Verschiebung um $T$/2) zustande. Die vorher gezeigte rein reelle si–Funktion würde hingegen dem nichtkausalen Rechteck von –$T$/2 bis +$T$/2 entsprechen.

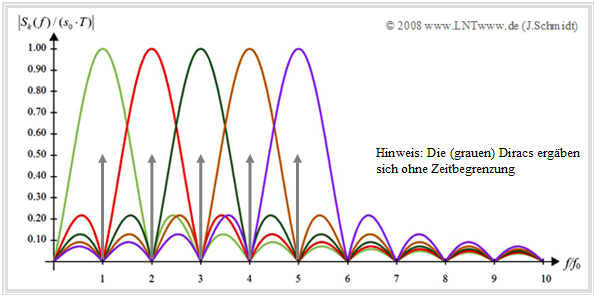
Die Grafik zeigt exemplarisch das Betragsspektrum eines OFDM–Signals mit fünf Trägern.

Auffallend ist, dass das Maximum eines jeden Subträgers mit den Nullstellen aller anderen Träger zusammenfällt. Dies entspricht der ersten Nyquistbedingung im Frequenzbereich. Diese Eigenschaft ermöglicht eine ICI–freie Abtastung (das heißt: ohne Intercarrier–Interferenz) des Spektrums bei Vielfachen von $f_0$. Die Orthogonalität ist also gewährleistet.

Fazit: Ein OFDM–Signal unter der Voraussetzung einer rechteckförmigen Impulsformung und eines Unterträgerabstandes von $f_0$ erfüllt die erste Nyquistbedingung im Zeit– und Frequenzbereich.

Würde man auf die Zeitbegrenzung bei der Impulsformung verzichten, so würden aus den dargestellten si–Funktionen im Abstand $f_0$ jeweils Diraclinien (in der Grafik grau eingezeichnet). Diese idealisierende Vereinfachung ist in der Praxis leider nicht umsetzbar. Die Forderung $T → ∞$ bedeutet nämlich gleichzeitig, dass in unendlich langer Zeit nur ein einziger Rahmen übertragen werden könnte.

Orthogonalitätseigenschaften der Träger

Die Zeitbegrenzung des Grundimpulses ermöglicht die separate Betrachtung der beiden Summen in der Gleichung des OFDM–Sendesignals: $$s(t) = \sum\limits_{k = - \infty }^{+\infty} {s_k (t)} \quad {\rm{mit}} \quad s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,k} \cdot g_\mu (t - k \cdot T )}.$$ Der $k$–te Sendeimpuls ist dabei die Summe der um $k · T$ verschobenen Grundimpulse $g_{\mu}(t)$, die jeweils mit den $\mu$–ten Amplitudenkoeffizienten des QAM–Coders zum Zeitpunkt $k$ gewichtet werden. Damit ergibt sich für das Spektrum $S_{\mu,k}(f)$ des $\mu$–ten Trägers im $k$–ten Intervall: $$S_{\mu ,k} (f) = s_0 \cdot a_{\mu ,k} \cdot T \cdot {\rm{si}}(\pi \cdot T(f - \mu \cdot f_0 )) \cdot {\rm{e}}^{ - {\rm{j\pi}}T (f - \mu \cdot f_0)}.$$ Es gilt:

• Die Sendeimpulse $s_k(t)$ sind zueinander orthogonal in der Zeit (Laufvariable $k$), da sie sich durch die Zeitbegrenzung des Impulsformfilters $g_s(t)$ zeitlich nicht überlappen.
• Die zeitliche Begrenzung der Impulse führt zwar zu einer spektralen Überlappung, aber dennoch besteht auch Orthogonalität bezüglich der Träger (Laufvariable $\mu$) wegen:

$$S_k (\mu \cdot f_0 ) = S_{\mu ,k} (\mu \cdot f_0 ) = s_0 \cdot a_{\mu ,k} \cdot T$$

Fazit: Die Orthogonalität des OFDM–Signals $s(t)$ ist

• sowohl für die Laufvariable $k$ (Zeit)
• als auch für die Laufvariable $\mu$ (Trägerfrequenzen)

gegeben. Diese Orthogonalitätseigenschaften wurden bereits in den vorhergehenden Abschnitten anhand von Grafiken verdeutlicht.

Nachfolgend folgt der Beweis der Trägerorthogonalität. Wenn Sie diesen überspringen wollen, so gehen Sie direkt zu Kapitel 5.6.

Beweis der Träger–Orthogonalität

Für die Orthogonalität an den Frequenzstützstellen $\mu · f_0$ muss gelten: $$S(\mu \cdot f_0 ) = S_0 (\mu \cdot f_0 ) + \ldots + S_\mu (\mu \cdot f_0 ) + \ldots + S_{N - 1} (\mu \cdot f_0 ) = S_\mu (\mu \cdot f_0 ).$$

Hier und im Folgenden wird auf den Index $k$ der Rahmennummer verzichtet. Aus $$s_\mu (t) = s_0 \cdot a_\mu \cdot {\rm{e}}^{{\rm j \hspace{0.03cm}\cdot\hspace{0.03cm}2\pi } \hspace{0.03cm}\cdot \hspace{0.03cm} \mu \hspace{0.03cm}\cdot \hspace{0.03cm} f_0 \hspace{0.03cm}\cdot \hspace{0.03cm} t} \cdot {\rm{rect}} \left( {\frac{ {t - T/2} }{T} } \right) \hspace{0.15cm} {\rm{und }} \hspace{0.15cm} S_\mu (f) = \int_{ - \infty }^{+\infty} {s_\mu (t) \cdot {\rm{e}}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi } \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t}$$

ergibt sich das Spektrum $S(f)$ allgemein zu: $$\begin{align*}S(f) & = \left( {s_0 \cdot a_0 \cdot T \cdot {\rm{si}}({\rm{\pi }}f T ) \cdot {\rm{e}}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} \frac{T}{2}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \int_{ - \infty }^{+\infty} {{\rm{e}}^{\rm{0}} \cdot {\rm{e}}^{ - {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }} \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t} \hspace{0.08cm}+ \ldots \\ & + \left( {s_0 \cdot a_\mu \cdot T \cdot {\rm{si}} ({\rm{\pi }} f T ) \cdot {\rm{e}}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} \frac{T}{2}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \int_{ - \infty }^{+\infty} {{\rm{e}}^{ {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }} \hspace{0.03cm}\cdot \hspace{0.03cm}\mu \hspace{0.03cm}\cdot \hspace{0.03cm} f_0 \hspace{0.03cm}\cdot \hspace{0.03cm} t} \cdot {\rm{e}}^{ - {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }} \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t} \hspace{0.08cm}+ \ldots \\ & +\left( {s_0 \cdot a_{N - 1} \cdot T \cdot {\rm{si}} ({\rm{\pi }}f T ) \cdot {\rm{e}}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} \frac{T}{2}\hspace{0.03cm}\cdot \hspace{0.03cm} f} }\right) * \int_{ - \infty }^{+\infty} {{\rm{e}}^{{\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }} \hspace{0.03cm}\cdot \hspace{0.03cm}(N-1) \hspace{0.03cm}\cdot \hspace{0.03cm} f_0 \hspace{0.03cm}\cdot \hspace{0.03cm} t} \cdot {\rm{e}}^{ - {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi }} \hspace{0.03cm}\cdot \hspace{0.03cm} f \hspace{0.03cm}\cdot \hspace{0.03cm} t} \hspace{0.06cm}{\rm d}t} .\end{align*}\\$$

Mit Distributionen lässt sich diese Gleichung wie folgt ausdrücken: $$\begin{align*}S(f) & = \left( {s_0 \cdot a_0 \cdot T \cdot {\rm{si}}({\rm{\pi }}f T ) \cdot {\rm{e}}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \delta (f) \hspace{0.08cm}+ \ldots \\ & + \left( {s_0 \cdot a_\mu \cdot T \cdot {\rm{si}} ({\rm{\pi }} fT )\cdot {\rm{e}}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \right) * \delta (f - \mu \cdot f_0 )\hspace{0.08cm}+ \ldots \\ & + \left( {s_0 \cdot a_{N - 1} \cdot T \cdot {\rm{si}} ({\rm{\pi }} f T ) \cdot {\rm{e}}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} }\right) * \delta (f-(N - 1) \cdot f_0 ) .\end{align*}\\$$ $$\begin{align*}\Rightarrow \hspace{0.3cm}S(f) & = {s_0 \cdot a_0 \cdot T \cdot {\rm{si}}({\rm{\pi }} \cdot T \cdot f) \cdot {\rm{e}}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} f} } \hspace{0.08cm}+\hspace{0.08cm} \ldots \\ & + {s_0 \cdot a_\mu \cdot T \cdot {\rm{si}} ({\rm{\pi }} \cdot T \cdot (f - \mu \cdot f_0 ))\cdot {\rm{e}}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} (f - \mu \hspace{0.03cm}\cdot \hspace{0.03cm}f_0 )} } \hspace{0.08cm}+ \hspace{0.08cm}\ldots \\ & + {s_0 \cdot a_{N - 1} \cdot T \cdot {\rm{si}} ({\rm{\pi }} \cdot T \cdot (f-(N - 1) \cdot f_0 )) \cdot {\rm{e}}^{ - {\rm j \hspace{0.03cm}\cdot \hspace{0.03cm}\pi }\hspace{0.03cm}\cdot \hspace{0.03cm} {T}\hspace{0.03cm}\cdot \hspace{0.03cm} (f-(N - 1) \hspace{0.03cm}\cdot \hspace{0.03cm}f_0 )} } .\end{align*}\\$$

Setzt man nun $f = \mu · f_0$, so erhält man: $$S (\mu \cdot f_0) = 0 \hspace{0.08cm}+ \hspace{0.08cm} \ldots \hspace{0.08cm}+\hspace{0.08cm} s_0 \cdot a_\mu \cdot T \cdot {\rm{si}} (0) \cdot {\rm{e}}^0 \hspace{0.08cm}+\hspace{0.08cm} \ldots + 0 = s_0 \cdot a_\mu \cdot T = S_\mu ( \mu \cdot f_0 ).$$

Das Spektrum bei $f = \mu · f_0$ setzt sich also nur aus Anteilen des $\mu$–ten Trägers zusammen, wobei alle anderen Träger identisch Null werden. Die Orthogonalität ist gewährleistet.

q.e.d.