Aufgabe 1.4: Zum Tiefpass 2. Ordnung
In Aufgabe A1.1 und Aufgabe Z1.1 im Kapitel 1.1 wurden die sog. RC–Tiefpässe im Frequenzbereich beschrieben. Hier soll nun eine Zeitbereichsdarstellung erfolgen.
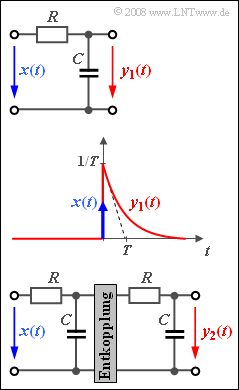
Die oben skizzierte Schaltung mit dem Eingangssignal $x(t)$ und dem Ausgangssignal $y_1(t)$ ist ein Tiefpass erster Ordnung mit dem Frequenzgang $$H_{\rm 1}(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm 0}}.$$
Hierbei gibt $f_0 = 1/(2πRC)$ die 3dB–Grenzfrequenz an. Legt man am Eingang ein diracförmiges Signal $x(t) = δ(t)$ an, so erscheint am Ausgang das Signal $y_1(t)$ gemäß der mittleren Skizze.
Der Zusammenhang zwischen den Systemparametern $R, C$ und $T$ lautet (siehe auch Aufgabe Z1.3): $$T = \frac{1}{\omega_{\rm 0}}= \frac{1}{2\pi f_{\rm 0}} = R C.$$ Für numerische Berechnungen soll im Folgenden $T =$ 1 ms verwendet werden.
Die untere Schaltung mit Eingang $x(t)$ und Ausgang $y_2(t)$ zeigt einen Tiefpass zweiter Ordnung: $$H_{\rm 2}(f) = [H_{\rm 1}(f)]^2 =\frac{1}{(1+{\rm j}\cdot f/f_{\rm 0})^2}.$$ Die zu $H_2(f)$ gehörende Impulsantwort ist $h_2(t)$.
Anzumerken ist, dass der Systemparameter $f_0$ bei einem Tiefpass zweiter oder höherer Ordnung nicht mehr dessen 3 dB–Grenzfrequenz angibt. Weiterhin ist noch zu beachten, dass die beiden RC-Glieder entkoppelt werden müssen, um Widerstandsanpassung zu erreichen. Hierzu eignet sich zum Beispiel ein Operationsverstärker. Dieser Hinweis ist jedoch für die Lösung dieser Aufgabe nicht relevant.
Hinweis: Die Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.2. Zur Lösung dieser Aufgabe können Sie das folgende unbestimmte Integral verwenden: $$\int u \cdot {\rm e}^{a \cdot \hspace{0.03cm} u} \hspace{0.1cm}{\rm d}u = \frac{{\rm e}^{\hspace{0.03cm}a \cdot \hspace{0.03cm} u}}{a^2} \cdot (a \cdot u -1).$$
Fragebogen
Musterlösung
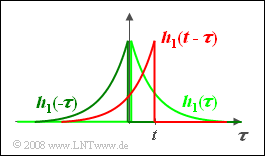
$$y_1(t) = x (t) * h_1 (t) = T \cdot \left[ h_1 (t) * h_1 (t) \right].$$ Die Faltung ist für einen spezifischen Zeitpunkt $t$ in nebenstehender Skizze verdeutlicht.
Nach Variablenumbenennung erhält man: $$\begin{align*}h_1(\tau) & = \frac{1}{T} \cdot {\rm e}^{-\tau/T}\hspace{0.1cm} \Rightarrow \hspace{0.1cm}h_1(-\tau) = \frac{1}{T} \cdot {\rm e}^{\tau/T}\hspace{0.1cm} \Rightarrow \hspace{0.1cm}h_1(t-\tau) = \frac{1}{T} \cdot {\rm e}^{(-t+\tau)/T} \\ & \Rightarrow\hspace{0.5cm} y_1(t) = T \cdot \int\limits_{ - \infty }^{ + \infty } h_1 ( {t - \tau } )\cdot {h_1 ( \tau )} \hspace{0.1cm}{\rm d}\tau.\end{align*}$$ Für $τ < 0$ ist $h_1(τ) = 0$. Für $τ > t$ verschwindet der erste Faltungsoperand (siehe Skizze). Daraus folgt: $$y_1(t) = T \cdot \frac{1}{T^2}\cdot \int_{ 0 }^{ t } {\rm e}^{(-t+\tau)/T} \cdot {\rm e}^{-\tau/T} \hspace{0.1cm}{\rm d}\tau = \frac{1}{T}\cdot \int_{ 0 }^{ t } {\rm e}^{-t/T} \hspace{0.1cm}{\rm d}\tau .$$ Man sieht, dass nun der Integrand unabhängig von der Integrationsvariablen $τ$ ist. Somit gilt: $$y_1(t) =\frac{t}{T} \cdot {\rm e}^{-t/T}\hspace{0.1cm} \Rightarrow \hspace{0.1cm} y_1(t =0) \hspace{0.15cm}\underline{=0}; \hspace{0.5cm}y_1(t =T)={\rm e}^{-1} \hspace{0.15cm}\underline{=0.368}.$$
3. Aufgrund von $H_2(f) = H_1(f) · H_1(f)$ gilt für die Impulsantwort:
$$h_2(t) = h_1 (t) * h_1 (t).$$
Bis auf den zusätzlichen konstanten Faktor $1/T$ erhält man das gleiche Ergebnis wie unter 2):
$$h_2(t) =\frac{t}{T^2} \cdot {\rm e}^{-t/T}.$$
Der Maximalwert wird durch Nullsetzen der Ableitung ermittelt:
$$\begin{align*}\frac{{\rm d} h_2(t)}{{\rm d}t} & = \frac{1}{T^2} \cdot {\rm e}^{-t/T} \cdot \left( 1 - {t}/{T}\right) = 0 \hspace{0.7cm} \Rightarrow \hspace{0.7cm} t_{\rm 2} \hspace{0.15cm}\underline{= T = 1\,\,{\rm ms}} \\ & \Rightarrow \hspace{0.1cm} h_2(t_{\rm 2}) =\frac{{\rm e}^{-1}}{T} =\frac{0.368}{1\,\,{\rm ms}} \hspace{0.15cm}\underline{ = {\rm 368 \hspace{0.1cm} 1/s}}.\end{align*}$$
4. Allgemein bzw. mit dem Ergebnis aus 3) gilt für die Sprungantwort:
$${\rm \sigma_2}(t) = \int_{ 0 }^{ t } {h_2 ( \tau )} \hspace{0.1cm}{\rm d}\tau =
\frac{1}{T^2} \cdot \int_{ 0 }^{ t } \tau \cdot {\rm e}^{-\tau/T} \hspace{0.1cm}{\rm d}\tau .$$
Mit der Substitution $u = τ/T$ folgt daraus unter Verwendung des angegebenen Integrals:
$$\begin{align*}{\rm \sigma_2}(t) & = \int_{ 0 }^{ t /T} u \cdot {\rm e}^{-u} \hspace{0.1cm}{\rm d}u ={\rm e}^{-u} \cdot (-u-1) |_{ 0 }^{ t /T}. \\ & \Rightarrow \hspace{0.1cm}{\rm \sigma_2}(t) =
1- \left( 1 + {t}/{T} \right) \cdot {\rm e}^{-t/T}.\end{align*}$$
Zu den angegebenen Zeitpunkten erhält man unter weiterer Berücksichtigung des Faktors 2V:
$$\begin{align*}y_2(t = T) & = {\rm 2 \,V} \cdot \left( 1- 2 \cdot {\rm e}^{-1} \right) \hspace{0.15cm}\underline{= {\rm 0.528 \,V}}, \\ y_2(t = 5T) & = {\rm 2 \,V} \cdot \left( 1- 6 \cdot {\rm e}^{-5} \right) \hspace{0.15cm}\underline{= {\rm 1.919 \,V}}.\end{align*}$$
Für noch größere Zeiten nähert sich $y_2(t)$ immer mehr dem Endwert 2V an.