Aufgabe 1.6: Rechteckförmige Impulsantwort
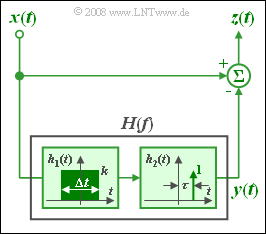
Wir betrachten im Folgenden die in der Grafik gezeigte Konstellation. Der Frequenzgang $H(f) = H_1(f) · H_2(f)$ im unteren Zweig ist durch die Impulsantworten seiner beiden Teilkomponenten festgelegt. Hierbei ist $h_1(t)$ im Bereich von –1 ms bis 1 ms konstant gleich $k$ und außerhalb 0; an den Bereichsgrenzen gilt jeweils der halbe Wert. Die im Bild eingezeichnete Zeitvariable ist somit $Δt =$ 2 ms.
Die Impulsantwort der zweiten Systemfunktion $H_2(f)$ lautet:
$$h_2(t) = \delta(t - \tau).$$
Der Frequenzgang zwischen den Signalen $x(t)$ und $z(t)$ hat Hochpass–Charakter und lautet allgemein:
$$H_{\rm HP}(f) = 1 - H_1(f) \cdot {\rm e}^{-{\rm j2 \pi}f \tau}.$$
Für die Teilaufgaben a) bis d) gelte $τ =$ 0 und damit $H(f) = H_1(f)$. Mit dem Parameter $τ =$ 0 kann hierfür auch geschrieben werden ( $Δt =$ 2 ms):
$$H_{\rm HP}(f) = 1 - {\rm si}( \pi \cdot {\rm \Delta}t \cdot f).$$
Ohne Auswirkung auf die Lösung der Aufgabe ist anzumerken, dass diese Gleichung für $τ ≠$ 0 nicht anwendbar ist:
$$|H_{\rm HP}(f)|\hspace{0.09cm} \ne \hspace{0.09cm}1 - |H_1(f)| .$$
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.3.
Fragebogen
Musterlösung
2. Das Ausgangssignal $y(t)$ ergibt sich als das Faltungsprodukt von $x(t)$ und $h(t)$. Die Faltung zweier gleich breiter Rechtecke ergibt ein Dreieck mit dem Maximum bei $t =$ 0:
$$y(t = 0 ) = 1\hspace{0.05cm}{\rm V}\cdot \int\limits_{ - 1\,{\rm ms} }^{ 1\,{\rm ms} } {k \hspace{0.1cm}}{\rm d}\tau =
1\hspace{0.05cm}{\rm V}\cdot \int\limits_{ - 1\,{\rm ms} }^{ 1\,{\rm ms} } {\frac{1}{2\,{\rm ms}} \hspace{0.1cm}}{\rm d}\tau= 1\hspace{0.05cm}{\rm V}.$$
Richtig sind somit die $\rm \underline{ \ Vorschläge \ 2 \ und \ 4}$.
3.
4.
5.
6.
7.