Aufgabe 2.4: Frequenz– und Phasenversatz
Betrachtet wird das Quellensignal $$q(t) = A_{\rm 1} \cdot \cos(2 \pi f_{\rm 1} t ) +A_{\rm 2} \cdot \sin(2 \pi f_{\rm 2} t )$$ mit den Signalparametern $$ A_1 = 2\,{\rm V}, \hspace{0.15cm}f_1 = 2\,{\rm kHz}, \hspace{0.15cm}$$ $$A_2 = 1\,{\rm V}, \hspace{0.15cm}f_2 = 5\,{\rm kHz}\hspace{0.05cm}.$$ Dieses Signal wird ZSB–amplitudenmoduliert.
Das modulierte Signal $s(t)$ besitzt somit Spektralanteile bei $±45 kHz$, $±48 kHz$, $±52 kHz$ und $±55 kHz$. Bekannt ist weiter, dass das sendeseitige Trägersignal einen sinusförmigen Verlauf hat ($ϕ_T = –90°$).
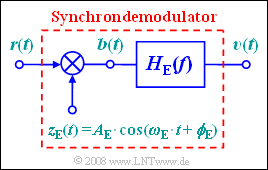
Die Demodulation soll mit nebenstehend skizzierter Schaltung erfolgen, die durch folgende Parameter bestimmt ist:
- Amplitude $A_E$ (ohne Einheit),
- Frequenz $f_E$,
- Phase $ϕ_E$.
Der Block $H_E(f)$ beschreibt einen idealen, rechteckförmigen Tiefpass, der geeignet dimensioniert ist.
Hinweis: Diese Aufgabe gehört zum Themengebiet von Kapitel 2.2. Berücksichtigen Sie die folgenden trigonometrischen Umformungen:
$$\\cos(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) + \cos(\alpha+\beta)\right] \hspace{0.05cm},$$
$$\\sin(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \sin(\alpha-\beta) + \sin(\alpha+\beta)\right] \hspace{0.05cm},$$
$$\\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right] \hspace{0.05cm}.$$
Fragebogen
Musterlösung