Aufgabe 2.7Z: ZSB-AM und Hüllkurvendemodulator
Ausgegangen wird vom Quellensignal $$ q(t) = 2 \,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t ) +$$ $$ + 2 \,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t )\hspace{0.05cm}.$$ Dieses wird entsprechend dem Modulationsverfahren „ZSB–AM mit Träger” moduliert und über einen idealen Kanal übertragen. Der Einfluss von Rauschen kann außer Acht gelassen werden.
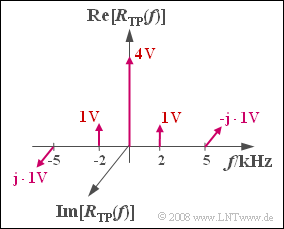
Die nebenstehende Grafik zeigt das Spektrum $R_{TP}(f)$ des Empfangssignals im äquivalenten Tiefpassbereich, das sich aus Diraclinien bei $f = 0$ (herrührend vom Träger), bei $±2 kHz$ (herrührend vom Cosinusanteil) und bei $±5 kHz$ (herrührend vom Sinusanteil) zusammensetzt.
Als Ortskurve bezeichnet man die Darstellung des äquivalenten Tiefpass–Signals $r_{TP}(t)$ in der komplexen Ebene, wobei $r_{TP}(t)$ die Fourierrücktransformierte von $R_{TP}(f)$ angibt.
Hinweis: Diese Aufgabe bezieht sich auf das Kapitel 2.3
Fragebogen
Musterlösung