Aufgabe 4.12Z: Nochmals 4–QAM–Systeme

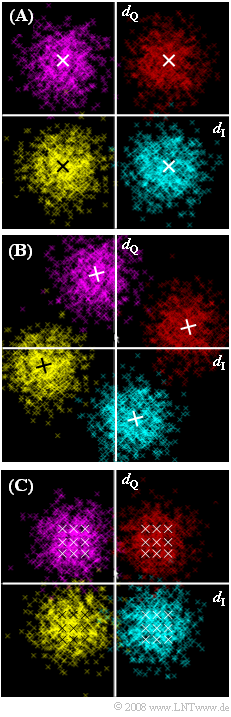
Die Grafik (A) zeigt das Phasendiagramm der 4–QAM nach dem Matched–Filter, wobei eine bei AWGN–Rauschen optimale Realisierungsform gewählt wurde:

rechteckförmiger Sendegrundimpuls der Symboldauer T,
rechteckförmige MF–Impulsantwort gleicher Breite T.

Dieses Phasendiagramm (A) bezieht sich ebenso wie die beiden anderen (B), (C) ausschließlich auf die Detektionszeitpunkte. Die Übergänge zwischen den einzelnen zeitdiskreten Punkten sind in diesem Phasendiagrammen dagegen nicht eingezeichnet.

Es liegt hier ein AWGN–Kanal mit $10 · lg E_B/N_0 = 9 dB$ vor. Entsprechend gilt für die Bitfehlerwahrscheinlichkeit des zunächst betrachteten Systems (A): $$p_{\rm B} = \frac{1}{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right )\hspace{0.05cm}.$$

Die Phasendiagramme (B) und (C) gehören zu zwei Systemen, bei denen die 4–QAM nicht optimal realisiert wurde. Auch hier ist AWGN–Rauschen mit $10 · lg E_B/N_0 = 9 dB$ vorausgesetzt.

Hinweis: Die Aufgabe bezieht sich auf das Themengebiet von Kapitel 4.3. Die Kreuze in den Grafiken markieren mögliche Punkte in den Phasendiagrammen, wenn kein AWGN–Rauschen vorhanden wäre. Als eine hinreichend gute Näherung für das komplementäre Gaußsche Fehlerintegral können Sie verwenden: $${\rm erfc}(x) \approx \frac{1}{\sqrt{\pi}\cdot x} \cdot {\rm e}^{-x^2}.$$

Fragebogen

$System (A): p_B$ =

$10^{-4}$

	Es besteht ein Phasenversatz zwischen Sender und Empfänger.
	Das Empfangsfilter führt zu Impulsinterferenzen.
	Es ergibt sich keine Degradation gegenüber System (A).

	Es besteht ein Phasenversatz zwischen Sender und Empfänger.
	Das Empfangsfilter führt zu Impulsinterferenzen.
	Es ergibt sich keine Degradation gegenüber System (A).

	(A), (B) und (C) haben gleiche Fehlerwahrscheinlichkeit.
	Die Fehlerwahrscheinlichkeit von System (A) ist am kleinsten.
	(B) besitzt eine größere Fehlerwahrscheinlichkeit als System (C).

Musterlösung

1. Aus der Angabe $10 · lg E_B/N_0 = 9 dB$ folgt: $${E_{\rm B}}/{N_0} = 10^{0.9}\approx 7.95 \hspace{0.05cm}.$$ Mit der angegebenen Näherung gilt weiter: $$p_{\rm B} = \frac{1}{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) \approx \frac{1}{2 \cdot\sqrt{\pi \cdot{E_{\rm B}}/{N_0}} } \cdot {\rm e}^{-{E_{\rm B}}/{N_0}} =$$ $$ = {1}/{2 \cdot\sqrt{7.95 \cdot \pi }} \cdot {\rm e}^{-7.95}\approx \hspace{0.15cm}\underline {0.35 \cdot 10^{-4}\hspace{0.05cm}}.$$ Der exakte Wert $p_B = 0.33 · 10^{–4}$ ist nur geringfügig kleiner.

2. Richtig ist der Lösungsvorschlag 1. Aufgrund eines Phasenversatzes um $Δϕ_T = 30°$ wurde das Phasendiagramm gedreht.

3. Insbesondere an den Kreuzen im Phasendiagramm (C), die den rauschfreien Fall markieren, erkennt man den Einfluss von Impulsinterferenzen. Anstelle des optimalen Empfangsfilters mit rechteckförmiger Impulsantwort wurde hier ein Gaußtiefpass mit der (normierten) Grenzfrequenz $f_G · T = 0.6$ verwendet, der Impulsinterferenzen bewirkt. Richtig ist hier der Lösungsvorschlag 2.

4. Die Systeme (B) und (C) sind nicht optimal. Daraus ist bereits ersichtlich, dass die Aussage 1 nicht zutrifft, sondern die Aussage 2. Jedes 4–QAM–System, das

dem Matched–Filter–Prinzip folgt und
zusätzlich die erste Nyquistbedingung erfüllt,

besitzt die vorne angegebene Fehlerwahrscheinlichkeit $$p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ).$$ Die so genannte „Wurzel–Nyquist–Konfiguration”, die zum Beispiel in der Aufgabe A4.11 behandelt wurde, hat somit die genau gleiche Fehlerwahrscheinlichkeit wie das System (A) und auch das gleiche Phasendiagramm zu den Detektionszeitpunkten. Die Übergänge zwischen den einzelnen Punkten sind jedoch unterschiedlich.

Auch die dritte Aussage ist zutreffend. Man erkennt bereits aus dem Phasendiagramm von System (B) Fehlentscheidungen und zwar immer dann, wenn Punkte farblich nicht zu den Quadranten passen. Die Ergebnisse einer Systemsimulation bestätigen diese Aussage:

$System (A): p_B ≈ 0.33 · 10^{–4}$ (siehe Teilaufgabe a),
$System (B): p_B ≈ 0.35 · 10^{–1},$
$System (C): p_B ≈ 0.24 · 10{–3}.$

Die Fehlerwahrscheinlichkeiten von System (B) und System (C) werden im Kapitel 1.5 des Buches „Digitalsignalübertragung” hergeleitet.