Aufgabe 5.3Z: Realisierung einer PN–Sequenz
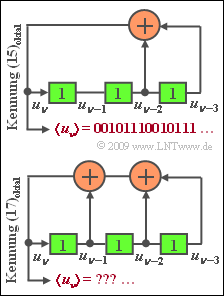
Die Grafik zeigt zwei mögliche Generatoren zur Erzeugung von PN–Sequenzen in unipolarer Darstellung: $u_ν$ ∈ {0, 1}. Der obere Generator mit den Koeffizienten $$ g_0 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_1 = 0 \hspace{0.05cm}, \hspace{0.2cm}g_2 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_3 = 1 \hspace{0.05cm}.$$ wird durch die Oktalkennung $(g_3, g_2, g_1, g_0)_{oktal} = (15)$ bezeichnet. Entsprechend ist die Oktalkennung des zweiten PN–Generators gleich (17).
Man spricht von einer M–Sequenz, wenn für die Periodenlänge der Folge 〈$u_ν$〉 gilt: $P = 2^G – 1$. Hierbei bezeichnet G den Grad des Schieberegisters, der gleich der Anzahl der Speicherzellen ist.
Hinweis: Die Aufgabe bezieht sich auf das Kapitel 5.3 dieses Buches sowie auf das Kapitel 2.5 im Buch „Stochastische Signaltheorie”. Wir möchten Sie gerne auch auf das folgende Lehrvideo hinweisen:
Verdeutlichung der PN–Generatoren (Dateigröße 982 kB – Dauer 5:08)
Fragebogen
Musterlösung