Allgemeine Beschreibung linearer Blockcodes

Inhaltsverzeichnis

1 Lineare Codes und zyklische Codes
2 Codefestlegung durch die Prüfmatrix
3 Codefestlegung durch die Generatormatrix
4 Systematische Codes (1)

Lineare Codes und zyklische Codes

Alle bisher behandelten Codes – Single Parity–check Code, Repetition Code und Hamming–Code – sind linear. Nun wird die für binäre Blockcodes gültige Definition von Linearität nachgereicht.

: Ein linearer Blockcode C ist ein Satz von 2^k Codeworten x = (x₁, x₂, ... , x_n), wobei die (Modulo–2)–Summe zweier beliebiger Codeworte x und x' wiederum ein gültiges Codewort ergibt:

\[\underline{x}, \underline{x}\hspace{0.05cm}' \in {\rm GF}(2^n),\hspace{0.3cm} \underline{x}, \underline{x}\hspace{0.05cm}' \in \mathcal{C} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{x} + \underline{x}\hspace{0.05cm}' \in \mathcal{C} \hspace{0.05cm}.\]

Diese Bedingung muss auch für x = x' erfüllt sein.

Hinweis: Die Modulo–Addition wird nun nicht mehr durch das Modulo–Additionszeichen ausgedrückt, sondern mit dem herkömmlichen Pluszeichen. Diese Vereinfachung der Schreibweise wird für den Rest dieses Buches beibehalten.

: Wir betrachten zwei (3, 2)–Blockcodes:

\[\mathcal{C}_1 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 0, 1) \hspace{0.05cm},(1, 1, 0) \}\hspace{0.05cm},\]

\[\mathcal{C}_2 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 1, 0) \hspace{0.05cm},(1, 1, 1) \hspace{0.05cm}.\]

Man erkennt:

Der Code C₁ ist linear, da die Modulo–2–Addition zweier beliebiger Codeworte stets auch ein gültiges Codewort ergibt, zum Beispiel (0, 1, 1) + (1, 0, 1) = (1, 1, 0).

Die obige Definition gilt auch für die Modulo–2–Addition eines Codewortes mit sich selbst, zum Beispiel (0, 1, 1) + (0, 1, 1) = (0, 0, 0) ⇒ Jeder lineare Code beinhaltet das Nullwort.

Obwohl die letzte Voraussetzung erfüllt wird, ist C₂ kein linearer Code. Für diesen Code gilt nämlich beispielsweise: (0, 1, 1) + (1, 1, 0) = (1, 0, 1). Dies ist kein gültiges Codewort von C₂.

Im Folgenden beschränken wir uns ausschließlich auf lineare Codes, da nichtlineare Codes für die Praxis von untergeordneter Bedeutung sind.

: Ein linearer Blockcode C heißt zyklisch, wenn eine jede zyklische Verschiebung eines Codewortes x (nach links oder rechts) wieder ein gültiges Codewort ergibt: \[\underline{x}= (x_1, x_2, ... \hspace{0.05cm}, x_n) \in \mathcal{C} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{x}\hspace{0.05cm}'= (x_n, x_1, ... \hspace{0.05cm}, x_{n-1}) \in \mathcal{C} \hspace{0.05cm}.\]

Man erkennt aus der Tabelle für den HC (7, 4, 3), dass dieser linear und zyklisch ist (schwarz: 4 Informationsbit, rot: n – k = 3 Prüfbit).

Außerdem ergibt sich auch dann ein gültiges Codewort, wenn man alle Bit invertiert: 0 ↔ 1. Auch das 0–Wort (n mal eine „0”) und das 1–Wort (n mal eine „1”) sind bei diesem Code zulässig.

Codefestlegung durch die Prüfmatrix

Wir betrachten den (7, 4, 3)–Hamming–Code mit Codeworten x der Länge n = 7, nämlich

den k = 4 Informationsbits x₁, x₂, x₃, x₄ , und

den m = 3 Prüfbits x₅, x₆, x₇.

Die Paritätsgleichungen lauten somit:

\[x_1 + x_2 + x_3 + x_5 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},\] \[x_2 + x_3 + x_4 + x_6 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},\] \[x_1 + x_2 + x_4 + x_7 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm}. \]

In der Matrixschreibweise lautet dieser Gleichungssatz:

\[{ \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} \hspace{0.05cm}. \]

In dieser Gleichung werden verwendet:

die Prüfmatrix H mit m = n – k = 3 Zeilen und n = 7 Spalten:

\[{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &0 &1 & 0 & 0\\ 0 &1 &1 &1 &0 & 1 & 0\\ 1 &1 &0 &1 &0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\]

das Codewort x = (x₁, x₂, ... , x₇) der Länge n = 7,

das Nullvektor 0 = (0, 0, 0) der Länge m = 3.

Durch Transponieren werden aus x und 0 die entsprechenden Spaltenvektoren x^T und 0^T.

:

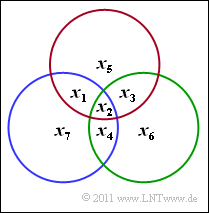
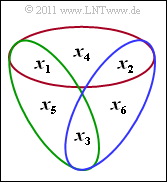
Die Grafik illustriert die m = 3 Paritätsgleichungen eines Codes C mit den Codeparametern n = 6 und k = 3 in der Reihenfolge rot, grün und blau. Entsprechend H · x^T = 0^T lautet die Prüfmatrix:

\[{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &0 &1 &0 & 0\\ 1 &0 &1 &0 &1 & 0\\ 0 &1 &1 &0 &0 & 1 \end{pmatrix}\hspace{0.05cm}.\]

Die 2^k = 8 Worte einer systematischen Realisierung dieses Codes lauten (mit den Prüfbits rechts vom kleinen Pfeil):

\[\underline{x}_0 \hspace{-0.1cm} = \hspace{-0.1cm} (0, 0, 0_{\hspace{0.01cm} \rightarrow} 0, 0, 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 0, 1_{\hspace{0.01cm} \rightarrow}0, 1, 1)\hspace{0.05cm},\hspace{0.2cm} \underline{x}_2 = (0, 1, 0_{\hspace{0.01cm} \rightarrow}1, 0, 1)\hspace{0.05cm},\] \[\underline{x}_3 \hspace{-0.1cm} = \hspace{-0.1cm} (0, 1, 1_{\hspace{0.01cm} \rightarrow}1, 1, 0)\hspace{0.05cm},\hspace{0.2cm} \underline{x}_4 = (1, 0, 0_{\hspace{0.01cm} \rightarrow} 1, 1, 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_5 = (1, 0, 1_{\hspace{0.01cm} \rightarrow}1, 0, 1)\hspace{0.05cm},\] \[\underline{x}_6 \hspace{-0.1cm} = \hspace{-0.1cm} (1, 1, 0_{\hspace{0.01cm} \rightarrow}0, 1, 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_7 = (1, 1, 1_{\hspace{0.01cm} \rightarrow}0, 0, 0)\hspace{0.05cm}.\]

Man erkennt aus diesen Angaben:

Die Anzahl der Spalten von H ist gleich der Codelänge n.

Die Anzahl der Zeilen von H ist gleich der Anzahl m = n – k der Prüfgleichungen.

Aus H · x^T = 0 folgt nicht, dass alle Codeworte eine gerade Anzahl von Einsen beinhalten.

Codefestlegung durch die Generatormatrix

Die Prüfmatrix H eines (n, k)–Blockcodes C hat m = n – k Zeilen und n Spalten. Den gleichen Code kann man aber auch durch die Generatormatrix G mit ebenfalls n Spalten, aber k Zeilen beschreiben:

: Ein linearer Blockcode C kann durch die Prüfmatrix H bzw. mit der Generatormatrix G wie folgt charakterisiert werden:

\[\mathcal{C} \hspace{-0.1cm} = \hspace{-0.1cm} \{ \underline{x} \in {\rm GF}(2^n): \hspace{0.2cm}{ \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} \}\hspace{0.05cm},\]

\[\mathcal{C} \hspace{-0.1cm} = \hspace{-0.1cm} \{ \underline{x} \in {\rm GF}(2^n)\hspace{0.05cm}, \hspace{0.1cm}\underline{u} \in {\rm GF}(2^k) : \hspace{0.2cm}\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \}\hspace{0.05cm}.\]

Bevor wir uns den Eigenschaften der Generatormatrix zuwenden, beschreiben wir an einem Beispiel die Erzeugung der Codeworte.

: Wir betrachten einen linearen (5, 3)–Blockcode mit der Generatormatrix

\[{ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &1 &0 &1 &1\\ 0 &1 &0 &1 &0\\ 0 &1 &1 &1 &0 \end{pmatrix} = \begin{pmatrix} \underline{g}_1\\ \underline{g}_2\\ \underline{g}_3\\ \end{pmatrix} \hspace{0.05cm}.\]

Damit werden die Informationsworte u = (u₁, u₂, u₃) den Codeworten x = (x₁, x₂, x₃, x₄, x₅) gemäß der folgenden Tabelle mit 8 Einträgen zugeordnet. Es gilt x = u · G.

\[\underline{u}_0 \hspace{-0.15cm} = \hspace{-0.15cm} (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_0 = (0, 0, 0, 0, 0) \hspace{0.05cm},\] \[\underline{u}_1 \hspace{-0.15cm} = \hspace{-0.15cm} (0, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_1 = (0, 1, 1, 1, 0) \hspace{0.1cm}= \hspace{0.1cm}\underline{g}_3\hspace{0.05cm},\] \[\underline{u}_2 \hspace{-0.15cm} = \hspace{-0.15cm} (0, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_2 = (0, 1, 0, 1, 0)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_2\hspace{0.05cm},\] \[\underline{u}_3 \hspace{-0.15cm} = \hspace{-0.15cm} (0, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_3 = (0, 0, 1, 0, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{g}_2+\underline{g}_3\hspace{0.05cm},\] \[\underline{u}_4 \hspace{-0.15cm} = \hspace{-0.15cm} (1, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_4 = (1, 1, 0, 1, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1 \hspace{0.05cm},\] \[\underline{u}_5 \hspace{-0.15cm} = \hspace{-0.15cm}(1, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_5 = (1, 0, 1, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+\underline{g}_3\hspace{0.05cm},\] \[\underline{u}_6 \hspace{-0.15cm} = \hspace{-0.15cm} (1, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_6 = (1, 0, 0, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+\underline{g}_2\hspace{0.05cm},\]

\[\underline{u}_7 \hspace{-0.15cm} = \hspace{-0.15cm} (1, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_7 = (1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+ \underline{g}_2+\underline{g}_3\hspace{0.05cm}.\]

Die hier zur Berechnung herangezogenen Basisvektoren g₁, g₂, g₃ – jeweils mit der Länge n = 5 – entsprechen den k = 3 Zeilen der Generatormatrix G. Anzumerken ist ferner, dass dieser Code wegen d_min = 1 weder zur Fehlerkorrektur noch zur Fehlererkennung geeignet ist. Trotzdem wird er auch auf den nächsten Seiten beispielhaft weiter betrachtet.

Hinweis: An dieser Stelle möchten wir Sie auf ein Interaktionsmodul zum Buch „Digitalsignalübertragung” aufmerksam machen, das die Bedeutung und Berechnung von Basisfunktionen vermittelt, wenn auch in völlig anderem Zusammenhang als in diesem Buch:

Gram–Schmidt–Verfahren Please add link and do not upload flash files.

Systematische Codes (1)

Die im Beispiel auf der letzten Seite verwendeten Vektoren g₁, g₂, ... , g_k sind die Basisvektoren des linearen Blockcodes C. Der Code selbst kann als k–dimensionaler Untervektorraum von GF(2ⁿ) angesehen werden. Die Basisvektoren g₁, g₂, ... , g_k sind linear unabhängig.

Der Untervektorraum C wird aber nicht nur durch die Basisvektoren

\[\underline{g}_1 = (1, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.3cm} \underline{g}_2 = (0, 1, 0, 1, 0) \hspace{0.05cm},\hspace{0.3cm} \underline{g}_3 = (0, 1, 1, 1, 0) \hspace{0.05cm}\]

aufgespannt, sondern andere Basisvektoren g'₁, g'₂ und g'₃ sind ebenso geeignet, so lange zwischen diesen die lineare Unabhängigkeit gewährleistet ist.

: Wir vergleichen die beiden Codes C und C' mit den Generatormatrizen

\[{ \boldsymbol{\rm G}} = \begin{pmatrix} \underline{g}_1\\ \underline{g}_2\\ \underline{g}_3\\ \end{pmatrix}= \begin{pmatrix} 1 &1 &0 &1 &1\\ 0 &1 &0 &1 &0\\ 0 &1 &1 &1 &0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}\hspace{0.05cm}'} = \begin{pmatrix} \underline{g}\hspace{0.05cm}'_1\\ \underline{g}\hspace{0.05cm}'_2\\ \underline{g}\hspace{0.05cm}'_3\\ \end{pmatrix}= \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0\\ 0 &0 &1 &0 &0 \end{pmatrix}\hspace{0.05cm}.\]

Die beiden Codes sind identisch: Sie beinhalten die genau gleichen Codeworte; es gilt nur eine andere Zuordnung. Bei dem Übergang von G auf G' wurden folgende erlaubte Operationen ausgeführt:

\[\underline{g}\hspace{0.05cm}'_1 = \underline{g}_1 + \underline{g}_2 \hspace{0.05cm},\hspace{0.3cm} \underline{g}\hspace{0.05cm}'_2 = \underline{g}_2 \hspace{0.05cm},\hspace{0.3cm} \underline{g}\hspace{0.05cm}'_3 = \underline{g}_2 + \underline{g}_3 \hspace{0.05cm}.\]

Zum entsprechenden Code C' kommt man mit der Gleichung x' = u · G.

\[\underline{u}_0 \hspace{-0.15cm} = \hspace{-0.15cm} (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_0 = (0, 0, 0, 0, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_0 \hspace{0.05cm},\] \[\underline{u}_1 \hspace{-0.15cm} = \hspace{-0.15cm} (0, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_1 = (0, 0, 1, 0, 0) \hspace{0.1cm}= \hspace{0.1cm}\underline{x}_3\hspace{0.05cm},\] \[\underline{u}_2 \hspace{-0.15cm} = \hspace{-0.15cm} (0, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_2 = (0, 1, 0, 1, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_2\hspace{0.05cm},\] \[\underline{u}_3 \hspace{-0.15cm} = \hspace{-0.15cm} (0, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_3 = (0, 1, 1, 1, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_1\hspace{0.05cm},\] \[\underline{u}_4 \hspace{-0.15cm} = \hspace{-0.15cm} (1, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_4 = (1, 0, 0, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_6 \hspace{0.05cm},\] \[\underline{u}_5 \hspace{-0.15cm} = \hspace{-0.15cm}(1, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_5 = (1, 0, 1, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_5\hspace{0.05cm},\] \[\underline{u}_6 \hspace{-0.15cm} = \hspace{-0.15cm} (1, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_6 = (1, 1, 0, 1, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_4\hspace{0.05cm},\] \[\underline{u}_7 \hspace{-0.15cm} = \hspace{-0.15cm} (1, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_7 = (1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_7\hspace{0.05cm}.\]

Die Codeworte x_i; beziehen sich auf die Generatormatrix G. Sie finden diese auf der letzten Seite.

Diese Codetabelle macht nochmals deutlich:

C und C' beinhalten die genau gleichen Codeworte. Sie sind damit identische Codes und besitzen beide die gleiche Korrekturfähigkeit (siehe nächste Seite).

C' ist aber nun ein systematischer Code, da die ersten k Binärstellen eines jeden Codewortes x' mit den Binärstellen des Informationswortes u übereinstimmen.