Codebeschreibung mit Zustands– und Trellisdiagramm

Zustandsdefinition für ein Speicherregister (1)

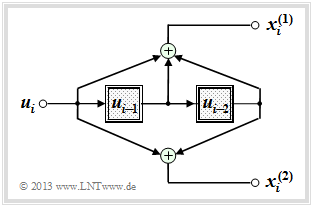
Ein Faltungscodierer kann auch als Automat mit endlicher Anzahl von Zuständen aufgefasst werden. Die Zustandsanzahl ergibt sich dabei aus der Zahl der Speicherelemente ⇒ Gedächtnis m zu 2^m.

Im Kapitel 3.3 gehen wir meist vom gezeichneten Faltungscodierer aus, der durch folgende Kenngrößen charakterisiert wird:

k = 1, n = 2 ⇒ Coderate R = 1/2,

Gedächtnis m = 2 ⇒ Einflusslänge ν = 3,

Übertragungsfunktionsmatrix in Oktalform (7, 5) ⇒ G(D) =(1 + D + D², 1 + D²).

Die Codesequenz zum Zeitpunkt i ⇒ x_i = (x_i⁽¹⁾, x_i⁽²⁾) hängt außer vom Informationsbit u_i auch vom Inhalt (u_i_–1, u_i_–2) des Speichers ab. Hierfür gibt es 2^m = 4 Möglichkeiten, die man als die Zustände S₀, S₁, S₂ und S₃ bezeichnet. Der Registerzustand S_μ sei dabei über den Index definiert:

\[\mu = u_{i-1} + 2 \cdot u_{i-2}\hspace{0.05cm}, \hspace{0.5cm}{\rm allgemein\hspace{-0.1cm}:}\hspace{0.15cm} \mu = \sum_{l = 1}^{m} \hspace{0.1cm}2\hspace{0.03cm}^{l-1} \cdot u_{i-l} \hspace{0.05cm}.\]

Im Englischen verwendet man für „Zustand” den Begriff State. Entsprechend ist auch im deutschen Text manchmal vom Registerstatus die Rede.

Um Verwechslungen zu vermeiden, unterscheiden wir im Weiteren durch Groß– bzw. Kleinbuchstaben:

die möglichen Zustände S_μ mit den Indizes 0 ≤ μ ≤ 2^m – 1,

die aktuellen Zustände s_i zu den Zeitpunkten i = 1, 2, 3, ....

Auf der nächsten Seite verdeutlichen wir die Zustände an einem Beispiel.

Zustandsdefinition für ein Speicherregister (2)

: Die folgende Grafik zeigt für obigen Faltungscodierer jeweils den Beginn (i ≤ 15)

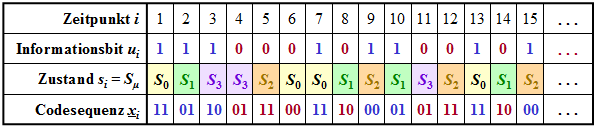
der Informationssequenz u ⇒ Informationsbits u_i,

der aktuellen Zustände s_i ∈ {S₀, S₁, S₂, S₃} zu den Zeitpunkten i, sowie

der jeweiligen Codesequenzen x_i = (x_i</sb>⁽¹⁾, x_i</sb>⁽²⁾).

Die Farbkennzeichnungen sollen den Übergang zu den nachfolgenden Grafiken auf den nächsten Seiten erleichtern. Man erkennt aus obiger Darstellung beispielsweise:

Zum Zeitpunkt i = 5 gilt u_i_–1 = u₄ = 0, u_i_–2 = u₃ = 1. Das heißt, der Automat befindet sich im Zustand s₅ = S₂. Mit dem Informationsbit u_i = u₅ = 0 erhält man die Codesequenz x₅ = (11).

Der Zustand für den Zeitpunkt i = 6 ergibt sich aus u_i_–1 = u₅ = 0 und u_i_–2 = u₄ = 0 zu s₆ = S₀. Wegen u₆ = 0 wird nun x₆ = (00) ausgegeben und der neue Zustand s₇ ist wiederum S₀.

Auch zum Zeitpunkt i = 12 wird wegen u₁₂ = 0 die Codesequenz x₁₂ = (11) ausgegeben und man geht vom Zustand s₁₂ = S₂ in den Zustand s₁₃ = S₀ über.

Dagegen wird zum Zeitpunkt i = 9 die Codesequenz (00) ausgegeben und auf <nobr>s₉ = S₂</nobr> folgt <nobr>s₁₀ = S₁.</nobr> Gleiches gilt auch für i = 15. In beiden Fällen lautet das aktuelle Informationsbit u_i = 1.

Aus diesem Beispiel ist zu erkennen, dass die Codesequenz x_i zum Zeitpunkt i allein

vom aktuellen Zustand s_i = S_μ (0 ≤ μ ≤ 2^m – 1), sowie

vom aktuellen Informationsbit u_i

abhängt. Ebenso wird der Nachfolgezustand s_i₊₁ allein durch s_i und u_i bestimmt. Diese Eigenschaften werden im so genannten Zustandsübergangsdiagramm auf der nächsten Seite berücksichtigt.