Grundlegendes zu den Low–density Parity–check Codes
Einige Charakteristika der LDPC–Codes (1)
Die Low–density Parity–check Codes – kurz LDPC–Codes – wurden bereits Anfang der 1960er Jahre erfunden und gehen auf die Dissertation [Gal63][1] von Robert G. Gallager zurück.
Die Idee kam allerdings aufgrund der damaligen Prozessorentechnologie um einige Jahrzehnte zu früh. Schon drei Jahre nach Berrou's Erfindung der Turbocodes 1993 erkannten dann allerdings David J. C. MacKay und Radford M. Neal das riesige Potential der LDPC–Codes, wenn man diese ebenso wie die Turbocodes iterativ symbolweise decodiert. Sie erfanden die LDPC–Codes quasi neu.
Wie aus dem Namensbestandteil „Parity–check” bereits hervorgeht, handelt es sich bei diesen Codes um lineare Blockcodes entsprechend den Ausführungen in Kapitel 1. Deshalb gilt auch hier:
- Das Codewort ergibt sich aus dem Informationswort u (dargestellt mit k Binärsymbolen) und der Generatormatrix G der Dimension k×n zu x = u · G ⇒ Codewortlänge n.
- Die Prüfgleichungen ergeben sich aus der Identität x · HT ≡ 0, wobei H die Prüfmatrix bezeichnet. Diese besteht aus m Zeilen und n Spalten. Während im ersten Kapitel grundsätzlich m = n – k gegolten hat, fordern wir für die LPDC–Codes lediglich noch m ≥ n – k.
Ein gravierender Unterschied zwischen einem LDPC–Code und einem herkömmlichen Blockcode nach der Beschreibung im ersten Kapitel ist, dass die Prüfmatrix H nur spärlich mit Einsen besetzt ist.
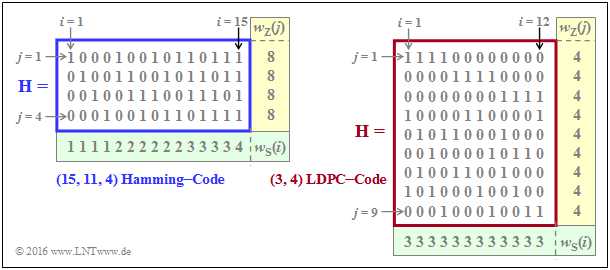
- den Hamming–Code mit Codelänge n = 15, m = 4 ⇒ k = 11 Informationsbits,
- den LDPC–Code aus [Liv15][2] der Länge n = 12 und mit m = 9 Prüfgleichungen ⇒ k ≥ 3.
In der linken Grafik beträgt der Anteil der Einsen 32/60 ≈ 53.3%, wohingegen in der rechten Grafik der Einsen–Anteil mit 36/108 = 33.3% geringer ist. Bei den für die Praxis relevanten LDPC–Codes (großer Länge) ist der Einsen–Anteil noch deutlich niedriger.
Einige Charakteristika der LDPC–Codes (2)
Wir analysieren nun die beiden Prüfmatrizen anhand der Rate und des Hamming–Gewichts.
- Die Rate des betrachteten Hamming–Codes (linke Grafik) ist R = k/n = 11/15 ≈ 0.733. Das Hamming–Gewicht einer jeden der vier Zeilen ist wZ = 8, während die Hamming–Gewichte wS(i) der Spalten zwischen 1 und 4 variieren. Für die Spalten–Laufvariable gilt hier: 1 ≤ i ≤ 15.
- Beim betrachteten LDPC–Code gibt es in allen Zeilen vier Einsen ⇒ wZ = 4 und in allen Spalten drei Einsen ⇒ wS = 3. Die Codebezeichnung (wZ, wS) LDPC–Code verwendet genau diese Parameter. Beachten Sie die unterschiedliche Nomenklatur zum „(n, k, m) Hamming–Code”.
- Man spricht hier von einem regulären LDPC–Code, da alle Zeilengewichte wZ(j) für 1 ≤ j ≤ m konstant gleich wZ sind und auch alle Spaltengewichte (mit den Indizes 1 ≤ i ≤ n) gleich sind: wS(i) = wS = const. Ist diese Bedingung nicht erfüllt, so liegt ein irregulärer LDPC–Code vor.
- Für die Coderate kann man allgemein (also, wenn k nicht bekannt ist) nur eine Schranke angeben: R ≥ 1 – wS/wZ. Das Gleichheitszeichen gilt dann, wenn alle Zeilen von H linear unabhängig sind ⇒ m = n – k. Dann ergibt sich die herkömmliche Gleichung: R = 1 – wS/wZ = 1 – m/n = k/n.
- Dagegen gilt für die Coderate eines irregulären LDPC–Codes und auch für den links skizzierten (15, 11, 4) Hammingcode:
- \[R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} \hspace{0.5cm}{\rm mit}\hspace{0.5cm} {\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n}w_{\rm S}(i) \hspace{0.5cm}{\rm und}\hspace{0.5cm} {\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{ m}w_{\rm Z}(j) \hspace{0.05cm}.\]
- Da beim Hamming–Code die m = n – k Prüfgleichungen linear voneinander unabhängig sind, kann das „≥”–Zeichen durch das Gleichheitszeichen ersetzt werden, was gleichzeitig R = k/n bedeutet.
Weitere Informationen zu diesem Thema finden Sie in Aufgabe A4.11 und in Aufgabe Z4.11