Aufgabe 3.4Z: Verschiedene Allpässe

Wir gehen zunächst von einem Vierpol mit der folgenden Übertragungsfunktion aus:

$$H_{\rm L}(p)= \frac {1-{p}/{A}} {1+{p}/{A}}.$$

Aus dieser soll der herkömmliche Fourier–Frequenzgang

$$H(f) = {\rm e}^{-a(f)\hspace{0.05cm}}\cdot {\rm e}^{- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}$$

ermittelt werden, der sich durch die Dämpfungsfunktion a(f) und die Phasenfunktion b(f) darstellen lässt.

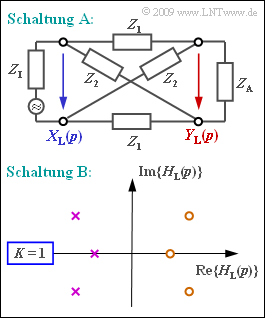
Die obere Grafik zeigt eine so genannte Allpass–Schaltung, wobei der komplexe Widerstand Z₁ eine Induktivität und Z₂ eine Kapazität bezeichnet:

$$Z_1 = p \cdot L\hspace{0.05cm},\hspace{0.2cm}Z_2 = \frac{1}{p \cdot C}\hspace{0.05cm}.$$

Bei reflexionsfreier Anpassung am Eingang und Ausgang mit

$$Z_{\rm I}=Z_{\rm A} = \sqrt{Z_1 \cdot Z_2} = \sqrt{{L}/{C}}$$

gilt für die p–Übertragungsfunktion der Schaltung A (siehe obere Grafik):

$$H_{\rm L}(p)= \frac {Y_{\rm L}(p)} {X_{\rm L}(p)}= \frac {Z_2-Z_1} {Z_1+2 \cdot \sqrt{Z_1 \cdot Z_2}+Z_2}\hspace{0.05cm}.$$

Die Schaltung B ist durch die p–Übertragungsfunktion festgelegt. Sie ist dadurch charakterisiert, dass alle Pole (in der linken p–Halbebene) spiegelbildlich zu den Nullstellen (in der rechten Halbebene) liegen.

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 3.2.

Fragebogen

$K$ = -

$p_o$ =

$\cdot A$

$p_x$ = -

$\cdot A$

	Die Dämpfungsfunktion a(f) zeigt Tiefpassverhalten.
	Die Dämpfungsfunktion a(f) ist konstant.
	Das obige Ergebnis gilt allgemein für p_x = – p_o.

$b(f = A/2 \pi)$ =

$Grad$

$b(f = A/ \pi)$ =

$Grad$

$b(f → ∞)$ =

$Grad$

	Die Dämpfung a(f) ist konstant gleich 0 (Np).
	Die Phase b(f) steigt linear mit der Frequenz f an.
	b(f) ist die Hilbert–Transformierte von a(f).

	Die Dämpfung a(f) ist konstant.
	Die Phasenfunktion b(f) hat bei f = 0 den Wert 0.

Musterlösung

1. Durch Umformung der angegebenen p–Übertragungsfunktion ergibt sich

$$H_{\rm L}(p)= \frac {1-{p}/{A}} {1+{p}/{A}}= -1 \cdot \frac {p-A} {p+A}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\hspace{0.15cm} \underline{K =- 1}, \hspace{0,2cm} \hspace{0.15cm} \underline{p_{\rm o}/A = 1} ,\hspace{0,2cm} \hspace{0.15cm} \underline{ p_{\rm x}/A = -1} \hspace{0.05cm} .$$

2. Setzt man p = j · 2πf, so erhält man:

$$H(f)= \frac {1-{\rm j \cdot 2\pi \it f}/A} {1+{\rm j \cdot 2\pi \it f}/A}\hspace{0.05cm} .$$

Der Betrag eines Quotienten ist gleich dem Quotienten der Beträge:

$$|H(f)|= \frac {|1-{{\rm j} \cdot 2\pi f}/A|} {|1+{\rm j \cdot 2\pi \it f}/A|}= \frac {\sqrt{1+(2\pi f/A)^2}} {\sqrt{1+(2\pi f/A)^2}}= 1$$

$$\Rightarrow \hspace{0.3cm} a(f)= -{\rm ln} \hspace{0.1cm} |H(f)|= 0\hspace{0.2cm}({\rm Np \hspace{0.2cm}oder \hspace{0.2cm}dB})\hspace{0.05cm} .$$

Richtig ist somit die Aussage 2. Auch die Aussage 3 ist richtig, wie aus der Theorieseite Grafische Ermittlung der Dämpfung zu ersehen ist.

3. Die Phasenfunktion b(f) kann wie folgt berechnet werden:

$$b(f)= -{\rm arc} \hspace{0.1cm} H(f) \hspace{0.25cm} = \hspace{0.2cm} {\rm arctan } \hspace{0.1cm}\frac {2\pi f}{A} - {\rm arctan } \hspace{0.1cm}\frac {-2\pi f}{A} = 2 \cdot {\rm arctan } \hspace{0.1cm}\frac {2\pi f}{A}:\\ b(f= \frac{A}{2\pi})\hspace{0.25cm} = \hspace{0.2cm}2 \cdot {\rm arctan } \hspace{0.1cm}(1) = 2 \cdot 45^\circ\hspace{0.15cm} \underline{ = 90^\circ}\hspace{0.05cm} ,\\ b(f= \frac{A}{\pi})\hspace{0.25cm} = \hspace{0.2cm}2 \cdot {\rm arctan } \hspace{0.1cm}(2) = 2 \cdot 63.4^\circ \hspace{0.15cm} \underline{= 126.8^\circ}\hspace{0.05cm} ,\\ b(f \rightarrow \infty)\hspace{0.25cm} = \hspace{0.2cm}2 \cdot {\rm arctan } \hspace{0.1cm}(\infty) = 2 \cdot 90^\circ \hspace{0.15cm} \underline{= 180^\circ}\hspace{0.05cm} .$$

Zu den gleichen Ergebnissen kommt man nach der Vorgehensweise entsprechend der Seite Grafische Ermittlung der Phase im Theorieteil.

4. Die angegebene p–Übertragungsfunktion lässt sich wie folgt darstellen:

$$H_{\rm L}(p)\hspace{0.25cm} = \hspace{0.2cm} \frac {Z_2-Z_1} {Z_1+2 \cdot \sqrt{Z_1 \cdot Z_2}+Z_2}=\\ \hspace{0.25cm} = \hspace{0.2cm} \frac {(\sqrt{Z_2}-\sqrt{Z_1})(\sqrt{Z_2}+\sqrt{Z_1})} {(\sqrt{Z_2}+\sqrt{Z_1})^2}= \frac {\sqrt{Z_2}-\sqrt{Z_1}} {\sqrt{Z_2}+\sqrt{Z_1}}\hspace{0.05cm}.$$

Mit Z₁ = p · L und Z₂ = 1/(pC) erhält man weiter:

$$H_{\rm L}(p)= \frac {\sqrt{{1}/(pC)}-\sqrt{pL}} {\sqrt{{1}/(pC)}+\sqrt{pL}} = \frac {1- p \cdot \sqrt{LC}} {1+ p \cdot \sqrt{LC}} = -1 \cdot \frac {p-\sqrt{{1}/(LC)}} {p+\sqrt{{1}/(LC)}}$$

$$\Rightarrow \hspace{0.3cm}A = \sqrt{{1}/(LC)}: \hspace{0.2cm}H_{\rm L}(p)= -1 \cdot \frac {p-A} {p+A}\hspace{0.05cm}.$$

Es ergibt sich die genau gleiche Übertragungsfunktion, wie in der Teilaufgabe 1) berechnet. Daraus folgt, dass nur die Aussage 1 richtig ist:

Der Dämpfungsverlauf ist a(f) = 0 (Np). Keine Frequenz wird gedämpft oder verstärkt. Man spricht deshalb auch von einem „Allpass”.

Die zweite Aussage ist falsch. Der Phasenverlauf b(f) ist nicht linear, sondern vielmehr wie in der Teilaufgabe 3) berechnet.

Die Hilbert–Transformierte der Konstanten a(f) = 0 müsste zur Phasenfunktion b(f) = 0 führen, wie in Kapitel 3.1 gezeigt. Das heißt, dass die Aussage 3 falsch ist.

Nur bei minimalphasigen Systemen hängen die Dämpfungsfunktion a(f) und Phasenfunktion b(f) über die Hilbert–Transformation zusammen.

Bei einem solchen Minimum–Phasen–System liegen aber alle Pole und Nullstellen in der linken p–Halbebene, was hier nicht zutrifft ⇒ ein Allpass ist kein Minimum–Phasen–System.

5. Beide Aussagen sind richtig. Wie bereits in der Teilaufgabe 2) festgestellt wurde, ergibt sich dann eine konstante Dämpfung, wenn es zu jedem Pol in der linken p–Halbebene eine entsprechende Nullstelle in der rechten Halbebene gibt ⇒ die Schaltung B zeigt ebenfalls Allpass–Charakteristik.

Da b(f) stets eine unsymmetrische Funktion ist, gilt b(f = 0) = 0 ganz allgemein, das heißt für jede Spektralfunktion H(f), deren Fourier–Rücktransformierte reell ist.