Aufgabe 2.4: Zum LZW-Algorithmus

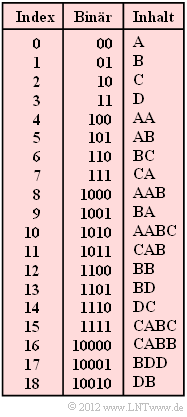
Der Komprimierungsalgorithmus LZW - benannt nach den Erfindern Abraham Lempel, Jacob Ziv und Terry Welch- arbeitet ebenso wie LZ78 mit einem globalen Wörterbuch. Dieses ist hier zu Beginn mit allen möglichen Zeichen – im Beispiel A, B, C und D – vorbelegt und wird während der Codierung sukzessive erweitert.

Bei der Decodierung entsteht genau das gleiche Wörterbuch, nur erfolgt der gleiche Eintrag mit dem Index I einen Schritt später als während der Codierung. Zur Bezeichnung der Decodierschritte verwenden wir hier die Laufvariable i.

Hier noch einige Hinweise zur LZW–Codierung und –Decodierung:

Bei der Codierung wird zu jedem Zeitpunkt i im Wörterbuch nach einer möglichst langen Zeichenkette gesucht, die mit dem aktuell anliegenden Eingabe–String übereinstimmt.

Der gefundene Wörterbuchindex I_i wird stets in Binärform übertragen. Gleichzeitig wird ins Wörterbuch unter dem nächsten freien Index W(I_i) + Z eingetragen.

Hierbei bezeichner W(I_i) ein Zeichen oder eine Zeichenfolge, und Z ist das erste Zeichen des anstehenden Eingabe–Strings (also ebenfalls ein Character), das in W(I_i) nicht mehr berücksichtigt ist.

Bei M = 4 möglichen Zeichen wird der erste Index I₁ mit 2 Bit übertragen, die Indizes I₂, ..., I₅ mit 3 Bit, die nächsten 8 Indizes mit 4 Bit, danach 16 Indizes mit 5 Bit usw. Die Begründung für diese bitsparende Maßnahme finden Sie in der Musterlösung zur Aufgabe.

Nach der Codierung in der hier beschriebenen Art und Weise über 16 Codierschritte ergibt sich die folgende Binärfolge der Länge N_Bit = 61:

$$\boldsymbol{\rm 00 000 001 010 100 0001 1000 0111 0001 0001 0011 1011 1011 01101 00011 01001}\hspace{0.05cm}.$$

Aufgabe des Decoders (genauer gesagt: Ihre Aufgabe) ist es nun,

aus dieser Binärsequenz die Indizes I₁, ... , I₁₆ zu rekonstruieren, wobei die unterschiedliche Bitanzahl zu berücksichtigen ist (Beschreibung der 16 Decodierergebnisse durch Dezimalzahlen),

anschließend aus dem Wörterbuch entsprechend den Indizes die zugehörigen Zeichen bzw. Zeichenfolgen auszulesen und schließlich – mit einem Schritt Verzögerung – den neuen Wörterbucheintrag zu generieren.

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 2.2.

Fragebogen

Musterlösung

1. Bei der LZW–Codierung des ersten Zeichens (i = 1) sind nur die vier Indizes I = 0, ... , I = 3 möglich, für die bereits zum Schritt i = 0 (Vorbelegung) ein Wörterbucheintrag vorgenommen wurde. Deshalb genügt es hier, den Index mit zwei Bit zu übertragen.

Bereits zum Schritt i = 2 werden dagegen drei Bit benötigt. Hätte die Eingangsfolge mit AAA begonnen, so hätte die LZW–Codierung I₂ = I(i = 2) den Dezimalwert 4 ergeben. Dieser ist nicht mehr mit zwei Bit darstellbar und muss mit drei Bit codiert werden, ebenso wie I₃, I₄ und I₅.

Der vorgegebene Eingabestring

$$\boldsymbol{\rm 00 000 001 010 100 0001}\hspace{0.05cm}...$$

ist deshalb vom Decoder wie folgt aufzuteilen:

$$\boldsymbol{\rm 00 | 000 |001 |010 |100 |0001|}\hspace{0.05cm}...$$

Die Decoderergebnisse der ersten vier Schritte lauten somit:

i = 1: I = 00 (binär) = 0 (dezimal) ⇒ A,

i = 2: I = 000 (binär) = 0 (dezimal) ⇒ A,

i = 3: I = 001 (binär) = 1 (dezimal) ⇒ B,

i = 4: I = 010 (binär) = 2 (dezimal) ⇒ C.

2. Berücksichtigt man, dass

für i = 1 zwei Bit verwendet werden,

für 2 ≤ i ≤ 5 drei Bit,

für 6 ≤ i ≤ 19 vier Bit,

für 14 ≤ i ≤ 29 fünf Bit,

so kommt man vom „kontinuierlichen Decoder–Eingangsstring”

$$\boldsymbol{\rm 00 000 001 010 100 0001 1000 0111 0001 0001 0011 1011 1011 01101 00011 01001}$$

zum „eingeteilten Decoder–Eingabestring” (erste Zeile I₁, ... , I₈, in der zweiten Zeile I₉, ... , I₁₆):

$$\boldsymbol{\rm 00 |000 |001 |010 |100 |0001 |1000 |0111 | }$$

$$\boldsymbol{\rm 0001 |0001 |0011 |1011 |1011 |01101 |00011 |01001} \hspace{0.1cm}.$$

Damit lauten die gesuchten Ergebnisse für die Decodierschritte i = 5, ... , i = 8:

i = 5: I = 100 (binär) = 4 (dezimal) ⇒ AA,

i = 6: I = 0001 (binär) = 1 (dezimal) ⇒ B,

i = 7: I = 1000 (binär) = 8 (dezimal) ⇒ AAB,

i = 8: I = 0111 (binär) = 7 (dezimal) ⇒ CA.

3. Richtig ist Aussage 2. Man erhält folgende Decodierergebnisse (in verkürzter Form):

I₉ = 1 ⇒ &nbsp B, I₁₀ = 1 ⇒ B, I₁₁ = 3 ⇒ D, I₁₂ = 11 ⇒ CAB,

I₁₃ = 11 ⇒ &nbsp CAB, I₁₄ = 13 ⇒ BD, I₁₅ = 3 ⇒ D, I₁₆ = 9 ⇒ BA.

4. Richtig sind die Aussagen 1 und 4, weil:

Der neu ankommende Index ist 18 (dezimal) und im Wörterbuch wird unter dem Index I = 18 der Eintrag DB gefunden.

Zum Decodierschritt i = 17 wird in das Wörterbuch die Zeile I = 19 eingetragen. Der Eintrag BAD setzt sich zusammen aus dem Decodierergebnis aus Schritt i = 16 (BA) und dem ersten Zeichen (D) des neuen Ergebnisses DB.

5. Richtig ist hier nur die Aussage 1:

Für die erste Phrase genügen zwei Bit.

Für die Phrasen I₂, ... , I₅ benötigt man drei Bit.

Für die Phrasen I₆, ... , I₁₃ benötigt man vier Bit.

Für die Phrasen I₁₄, ... , I₂₉ benötigt man fünf Bit.

Für die Phrasen I₃₀, ... , I₅₈ benötigt man sechs Bit.

Damit erhält man für die gesamte Bitanzahl:

$$N_{\rm Bit} = 1 \cdot 2 + 4 \cdot 3 + 8 \cdot 4 + 16 \cdot 5 + 29 \cdot 6 = 300 \hspace{0.05cm}.$$

Mit einheitlicher Bitlänge (6 Bit für jeden Index) wären 58 · 6 = 348 Bit (also mehr) erforderlich ⇒ Aussage 2 ist prinzipiell falsch. Nun zur Aussage 3:

Bei der uncodierten Übertragung von N = 150 Zeichen aus der Symbolmenge {A, B, C, D} würde man genau 300 Bit benötigen. Mit LZW benötigt man sicher mehr Bit, wenn die Quelle redundanzfrei ist (Zeichen gleichwahrscheinlich und statistisch unabhängig).

Bei redundanter Quelle mit (beispielsweise) H = 1.6 Bit/Quellensymbol kann man die Bitanzahl auf N_Bit = N · H begrenzen, vorausgesetzt, es handelt sich um eine sehr große Datei (N → ∞).

Bei einer eher kleinen Datei – wie hier lediglich mit N = 150 Bit – ist keine Aussage möglich, ob die Bitanzahl N_Bit kleiner, gleich oder größer als 150 · 1.6 = 240 sein wird. Auch N_Bit > 300 ist durchaus möglich. Dann sollte man auf die „LZ–Komprimierung” besser verzichten.

	Die Decoderausgabe zum Schritt i = 17 lautet DB.
	Die Decoderausgabe zum Schritt i = 17 lautet BAD.
	Neuer Wörterbucheintrag DB in die Zeile I = 19.
	Neuer Wörterbucheintrag BAD in die Zeile I = 19.

	AABCAABAABCAABCABBDBBDCDBA,
	AABCAABAABCABBDCABCABBDDBA,
	AABCAABAABCABDBBABCCDBAABDCDBA.

	Übertragen wurden 58 LZW–Phrasen mit variabler Bitlänge.
	Mit einheitlicher Indexbitlänge wären weniger Bit erforderlich.
	Übertragen wurde eine Datei mit N = 150 Quaternärzeichen.