Aufgabe 1.1Z: Redundanzfreie Binärquelle

• Zurück zum Buch

Eine jede digitale Quelle kann durch ihre Quellensymbolfolge $$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle$$ vollständig beschrieben werden, wobei hier entgegen dem Theorieteil die Laufvariable $\nu$ mit 0 beginnt. Entstammt jedes einzelne Symbol $q_\nu$ dem Symbolvorrat {L, H}, so spricht man von einer Binärquelle.

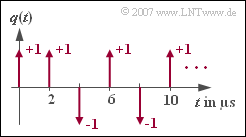
Unter Verwendung des Symbolabstandes $T$ kann man die Quellensymbolfolge $\langle q_\nu \rangle$ in äquivalenter Weise auch durch das diracförmige Quellensignal $$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T)$$

Fragebogen

1

{Wie groß ist der Symbolabstand?

$T$ = $\mu s$

2

Handelt es sich hierbei um die unipolare oder bipolare Repräsentation?

	Die Symbolfolge ist unipolar.
	Die Symbolfolge ist bipolar.

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)  (6)