Aufgabe 1.1: Dual-Slope–Verlustmodell

Zum Multiplexing beim GSM–Mobilfunksystem

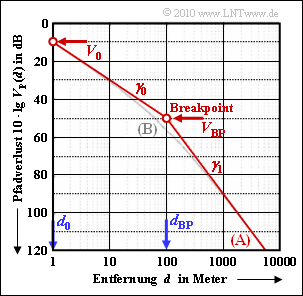
Zur Simulation des Pfadverlustes in städtischer Umgebung verwendet man oft das asymptotische Dual–Slope–Modell, das im Diagramm als rote Kurve dargestellt ist. Dieses einfache Modell ist durch zwei lineare Abschnitte gekennzeichnet, die durch den sog. Breakpoint (BP) getrennt sind:

Für $d ≤ d_{\rm BP}$ gilt mit dem Exponenten $\gamma_0$: $V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} ({d}/{d_0})\hspace{0.05cm}.$
Für $d > d_{\rm BP}$ ist der Pfadverlustexponent $\gamma_1$ anzusetzen, wobei $γ_1 > γ_0$ gilt: $V_{\rm P}(d) = V_{\rm BP} + \gamma_1 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} ({d}/{d_{\rm BP}})\hspace{0.05cm}.$

In diesen Gleichungen bedeuten:

$V_0$ ist der Pfadverlust (in dB) bei $d_0$ (Normierungsdistanz).
$V_{\rm BP}$ ist der Pfadverlust (in dB) bei $d=d_{\rm BP}$ ("Breakpoint").

Die Grafik gilt für die Modellparameter $d_0 = 1\,{\rm m}\hspace{0.05cm},\hspace{0.2cm}d_{\rm BP} = 100\,{\rm m}\hspace{0.05cm},\hspace{0.2cm} V_0 = 10\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm}\gamma_0 = 2 \hspace{0.05cm},\hspace{0.2cm}\gamma_1 = 4 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} V_{\rm BP} = 50\,{\rm dB}\hspace{0.05cm}.$

Fragebogen

Musterlösung

1. 2. 3. 4. 5. 6. 7.

	Falsch
	Richtig