Approximation der Fehlerwahrscheinlichkeit

1. Digitalsignalübertragung
2. Verallgemeinerte Beschreibung digitaler Modulationsverfahren
3. Approximation der Fehlerwahrscheinlichkeit

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Optimale Entscheidung bei binärer Übertragung

Wir gehen hier von einem Übertragungssystem aus, das wie folgt charakterisiert werden kann:   $\boldsymbol{r} = \boldsymbol{s} + \boldsymbol{n}$. Dieses System weist folgende Eigenschaften auf:

• Der das Übertragungssystem vollständig beschreibende Vektorraum wird von $N = 2$ zueinander orthogonalen Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ aufgespannt.
  

• Demzufolge ist auch die Wahrscheinlichkeitsdichtefunktion des additiven und weißen Gaußschen Rauschens zweidimensional anzusetzen, gekennzeichnet durch den Vektor $\boldsymbol{ n} = (n_1,\hspace{0.05cm}n_2)$.
  

• Es gibt nur zwei mögliche Sendesignale $(M = 2)$, die durch die beiden Vektoren $\boldsymbol{ s_0} = (s_{01},\hspace{0.05cm}s_{02})$ und $\boldsymbol{ s_1} = (s_{11},\hspace{0.05cm}s_{12})$ beschrieben werden:

$$s_0(t)= s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm},$$

$$s_1(t) = s_{11} \cdot \varphi_1(t) + s_{12} \cdot \varphi_2(t) \hspace{0.05cm}.$$

• Die beiden Nachrichten $m_0 \ \Leftrightarrow \ \boldsymbol{ s_0}$ und $m_1 \ \Leftrightarrow \ \boldsymbol{ s_1}$ sind nicht notwendigermaßen gleichwahrscheinlich.
  

• Aufgabe des Entscheiders ist es nun, für den gegebenen Empfangsvektor $\boldsymbol{r}$ einen Schätzwert nach der MAP–Entscheidungsregel anzugeben. Diese lautet im vorliegenden Fall:

$$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } |m_i ) ] \hspace{0.15cm} \in \hspace{0.15cm}\{ m_i\}\hspace{0.3cm}{\rm mit}\hspace{0.3cm} \boldsymbol{ r } = \boldsymbol{ \rho } = (\rho_1, \hspace{0.05cm}\rho_2) \hspace{0.05cm}.$$

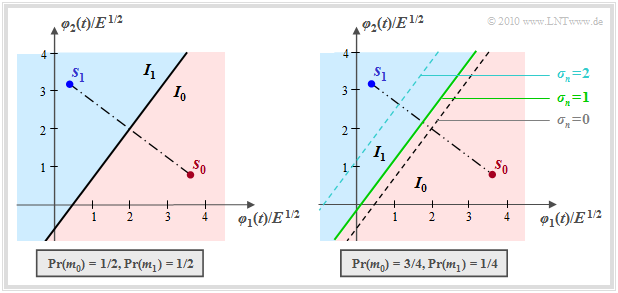
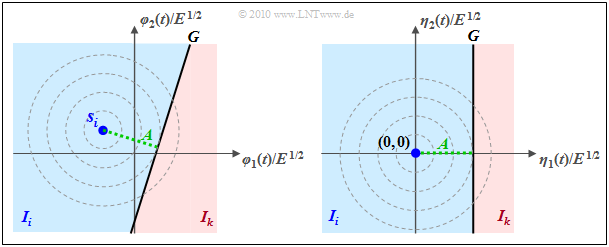
Im hier betrachteten Sonderfall $N = 2$ und $M = 2$ partitioniert der Entscheider den zweidimensionalen Raum in die zwei disjunkten Gebiete $I_0$ (rot hinterlegt) und $I_1$ (blau), wie die folgende Grafik verdeutlicht. Liegt der Empfangswert in $I_0$, so wird als Schätzwert $m_0$ ausgegeben, andernfalls $m_1$.

Entscheidungsregionen für gleiche (links) bzw. ungleiche (rechts) Auftrittswahrscheinlichkeiten

$\text{Herleitung und Bildbeschreibung:}$  Beim AWGN–Kanal und M = 2 lautet somit die Entscheidungsregel: Man entscheide sich immer dann für die Nachricht m₀, falls folgende Bedingung erfüllt ist:

$${\rm Pr}( m_0) \cdot {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot \vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 \right ] > {\rm Pr}( m_1) \cdot {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot\vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 \right ] \hspace{0.05cm}.$$

Die Grenzlinie zwischen den beiden Entscheidungsregionen $I_0$ und $I_1$ erhält man, wenn man in obiger Gleichung das Größerzeichen durch das Gleichheitszeichen ersetzt und die Gleichung etwas umformt:

$$\vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 - 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm}[{\rm Pr}( m_0)] = \vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 - 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm}[{\rm Pr}( m_1)]$$

$$\Rightarrow \hspace{0.3cm} \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 - \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 + 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}( m_0)}{ {\rm Pr}( m_1)} = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$

Aus dieser Gleichung erkennt man:

• Die Grenzkurve zwischen den Regionen $I_0$ und $I_1$ ist eine Gerade, da die Bestimmungsgleichung linear im Empfangsvektor $\boldsymbol{ \rho } = (\rho_1, \hspace{0.05cm}\rho_2)$ ist.
  

• Bei gleichwahrscheinlichen Symbolen verläuft die Grenze genau in der Mitte zwischen $\boldsymbol{ s }_0$ und $\boldsymbol{ s }_1$ und um $90^\circ$verdreht gegenüber der Verbindungslinie zwischen den Sendepunkten (linke Grafik):

$$\vert \hspace{-0.05cm} \vert \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert ^2 - \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert ^2 = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$

• Für ${\rm Pr}(m_0) > {\rm Pr}(m_1)$ ist die Entscheidungsgrenze in Richtung des unwahrscheinlicheren Symbols $\boldsymbol{ s }_1$ verschoben, und zwar um so mehr, je größer die AWGN–Streuung $\sigma_n$ ist.
  

• Die grün–durchgezogene Entscheidungsgrenze im rechten Bild sowie die Entscheidungsregionen $I_0$ (rot) und $I_1$ (blau) gelten für die (normierte) Streuung $\sigma_n = 1$ und die gestrichelten Grenzlinien für $\sigma_n = 0$ bzw. $\sigma_n = 2$.
  

Der Sonderfall gleichwahrscheinlicher Binärsymbolen

Wir gehen weiterhin von einem Binärsystem aus $(M = 2)$, betrachten aber nun den einfachen Fall, dass dieses durch eine einzige Basisfunktion beschrieben werden kann $(N = 1)$. Die Fehlerwahrscheinlichkeit hierfür wurde bereits im Abschnitt Definition der Bitfehlerwahrscheinlichkeit berechnet.

Mit der für das vierte Hauptkapitel gewählten Nomenklatur und Darstellungsform ergibt sich folgende Konstellation:

• Der Empfangswert $r = s + n$ ist nunmehr ein Skalar und setzt sich aus dem Sendesignal $s \in \{s_0, \hspace{0.05cm}s_1\}$ und dem Rauschterm $n$ zusammen. Die Abszisse $\rho$ bezeichnet eine Realisierung von $r$.
  

• Die Abszisse ist zudem auf die Bezugsgröße $E^{1/2}$ normiert, wobei hier die Normierungsenergie $E$ keine herausgehobene, physikalisch interpretierbare Bedeutung hat.
  

• Der Rauschterm $n$ ist gaußverteilt mit dem Mittelwert $m_n = 0$ und der Varianz $\sigma_n^2$. Die Wurzel aus der Varianz $(\sigma_n)$ wird als der Effektivwert oder die Streuung bezeichnet.
  

• Die Entscheidergrenze $G$ unterteilt den gesamten Wertebereich von $r$ in die beiden Teilbereiche $I_0$ (in dem unter anderem $s_0$ liegt) und $I_1$ (mit dem Signalwert $s_1$).
  

• Ist $\rho > G$, so liefert der Entscheider den Schätzwert $m_0$, andernfalls $m_1$. Hierbei ist vorausgesetzt, dass die Nachricht $m_i$ mit dem Sendesignal $s_i$ eineindeutig zusammenhängt:   $m_i \Leftrightarrow s_i$.

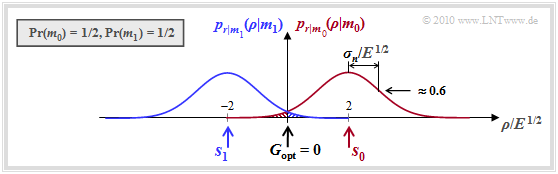
Die Grafik zeigt die bedingten (eindimensionalen) Wahrscheinlichkeitsdichtefunktionen $p_{\hspace{0.02cm}r\hspace{0.02cm} \vert \hspace{0.02cm}m_0}$ und $p_{\hspace{0.02cm}r\hspace{0.02cm} \vert \hspace{0.02cm}m_1}$ für den AWGN–Kanal, wobei gleiche Symbolwahrscheinlichkeiten vorausgesetzt sind:   ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 0.5$. Die (optimale) Entscheidergrenze ist somit $G = 0$.

Bedingte Dichtefunktionen bei gleichwahrscheinlichen Symbolen

Man erkennt aus dieser Darstellung:

• Ist $m = m_0$ und damit $s = s_0 = 2 \cdot E^{1/2}$, so kommt es nur dann zu einer Fehlentscheidung, wenn $\eta$, die Realisierung der Rauschgröße $n$, kleiner ist als $-2 \cdot E^{1/2}$. In diesem Fall ist $\rho < 0$, wobei $\rho$ eine Realisierung des Empfangswertes $r$ bezeichnet.
• Bei $m = m_1$   ⇒   $s = s_1 = -2 \cdot E^{1/2}$ kommt es dagegen immer dann zu einer Fehlentscheidung, wenn $\eta$ größer ist als $-2 \cdot E^{1/2}$. In diesem Fall ist $\rho > 0$.

Fehlerwahrscheinlichkeit bei gleichwahrscheinlichen Symbolen

Es gelte ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 0.5$. Bei AWGN–Rauschen mit dem Effektivwert (Streuung) $\sigma_n$ erhält man, wie bereits im Abschnitt Definition der Bitfehlerwahrscheinlichkeit mit anderer Nomenklatur berechnet wurde, für die Wahrschenlichkeit einer Fehlentscheidung $(\cal E)$ unter der Bedingung, dass die Nachricht $m_0$ gesendet wurde:

$${\rm Pr}({ \cal E}\hspace{0.02cm} \vert \hspace{0.02cm} m_0) = \int_{-\infty}^{G = 0} p_{r \hspace{0.05cm}|\hspace{0.05cm}m_0 } ({ \rho } \hspace{0.05cm} \vert \hspace{0.05cm}m_0 ) \,{\rm d} \rho = \int_{-\infty}^{- s_0 } p_{{ n} \hspace{0.05cm}\vert\hspace{0.05cm}m_0 } ({ \eta } |m_0 ) \,{\rm d} \eta = \int_{-\infty}^{- s_0 } p_{{ n} } ({ \eta } ) \,{\rm d} \eta = \int_{ s_0 }^{\infty} p_{{ n} } ({ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {s_0 }/{\sigma_n} \right ) \hspace{0.05cm}.$$

Bei der Herleitung der Gleichung wurde berücksichtigt, dass das AWGN–Rauschen $\eta$ unabhängig vom Signal ($m_0$ oder $m_1$) ist und eine symmetrische WDF besitzt. Verwendet wurde zudem das komplementäre Gaußsche Fehlerintegral

$${\rm Q}(x) = \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u \hspace{0.05cm}.$$

Entsprechend gilt für $m = m_1$   ⇒   $s = s_1 = -2 \cdot E^{1/2}$:

$${\rm Pr}({ \cal E} \hspace{0.02cm}\vert\hspace{0.02cm} m_1) = \int_{0}^{\infty} p_{{ r} \hspace{0.05cm}\vert\hspace{0.05cm}m_1 } ({ \rho } \hspace{0.05cm}\vert\hspace{0.05cm}m_1 ) \,{\rm d} \rho = \int_{- s_1 }^{\infty} p_{{ n} } (\boldsymbol{ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {- s_1 }/{\sigma_n} \right ) \hspace{0.05cm}.$$

$\text{Fazit:}$  Mit dem Abstand $d = s_1 - s_0$ der zwei Signalraumpunkte lassen sich die beiden Ergebnisse zusammenfassen, wobei noch ${\rm Pr}(m_0) + {\rm Pr}(m_1) = 1$ zu berücksichtigen ist:

$${\rm Pr}({ \cal E}\hspace{0.02cm}\vert\hspace{0.02cm} m_0) = {\rm Pr}({ \cal E} \hspace{0.02cm}\vert\hspace{0.02cm} m_1) = {\rm Q} \left ( {d}/(2{\sigma_n}) \right )$$

$$\Rightarrow \hspace{0.3cm}{\rm Pr}({ \cal E} ) = {\rm Pr}(m_0) \cdot {\rm Pr}({ \cal E} \hspace{0.02cm}\vert\hspace{0.02cm} m_0) + {\rm Pr}(m_1) \cdot {\rm Pr}({ \cal E} \hspace{0.02cm}\vert\hspace{0.02cm} m_1)= \left [ {\rm Pr}(m_0) + {\rm Pr}(m_1) \right ] \cdot {\rm Q} \left [ {d}/(2{\sigma_n}) \right ] = {\rm Q} \left [ {d}/(2{\sigma_n}) \right ] \hspace{0.05cm}.$$

Hinweise:

• Diese Gleichung gilt unter der Voraussetzung $G = 0$ ganz allgemein, also auch für ${\rm Pr}(m_0) \ne {\rm Pr}(m_1)$.
• Bei nicht gleichwahrscheinlichen Symbolen lässt sich allerdings die Fehlerwahrscheinlichkeit durch eine andere Entscheidergrenze verkleinern.
  
• Die hier genannte Gleichung gilt auch dann, wenn die Signalraumpunkte keine Skalare sind, sondern durch die Vektoren $\boldsymbol{ s}_0$ und $\boldsymbol{ s}_1$ beschrieben werden. Der Abstand $d$ ergibt sich dann als die Norm des Differenzvektors:   $d = \vert \hspace{-0.05cm} \vert \hspace{0.05cm} \boldsymbol{ s}_1 - \boldsymbol{ s}_0 \hspace{0.05cm} \vert \hspace{-0.05cm} \vert \hspace{0.05cm}.$

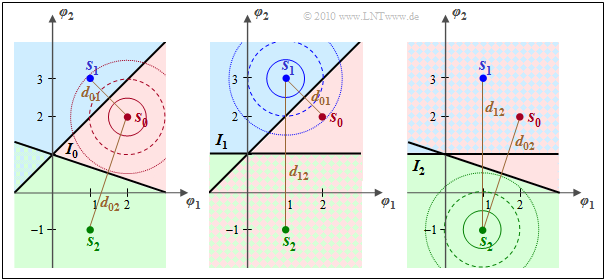
$\text{Beispiel 1:}$  Betrachten wir nochmals die Signalraumkonstellation von der ersten Kapitelseite (untere Grafik) mit den Werten

• $\boldsymbol{ s}_0/E^{1/2} = (3.6, \hspace{0.05cm}0.8)$ und
• $\boldsymbol{ s}_1/E^{1/2} = (0.4, \hspace{0.05cm}3.2)$.

Hier beträgt der Abstand der Signalraumpunkte

$$d = \vert \hspace{-0.05cm} \vert s_1 - s_0 \vert \hspace{-0.05cm} \vert = \sqrt{E \cdot (0.4 - 3.6)^2 + E \cdot (3.2 - 0.8)^2} = 4 \cdot \sqrt {E}\hspace{0.05cm}.$$

Zwei Signalraumkonstellationen

Es ergibt sich also der genau gleiche Wert wie für die obere Konstellation mit

• $\boldsymbol{ s}_0/E^{1/2} = (2, \hspace{0.05cm}0)$ und
• $\boldsymbol{ s}_1/E^{1/2} = (-2, \hspace{0.05cm}0)$.
  

Die Abbildungen zeigen diese beiden Konstellationen und lassen folgende Gemeinsamkeiten bzw. Unterschiede erkennen, wobei jeweils von der AWGN–Rauschvarianz $\sigma_n^2 = N_0/2$ ausgegangen wird. Die Kreise in der Grafik veranschaulichen die zirkuläre Symmetrie von 2D–AWGN–Rauschen.

• Wie bereits gesagt, sind sowohl der Abstand der Signalpunkte von der Entscheidungsgeraden $(d/2 = 2 \cdot \sqrt {E})$ als auch der AWGN–Kennwert $\sigma_n$ in beiden Fällen gleich.
  

• Daraus folgt: Die beiden Anordnungen führen zur gleichen Fehlerwahrscheinlichkeit, wenn man den Parameter $E$ (eine Art Normierungsenergie) konstant lässt:

$${\rm Pr} ({\rm Symbolfehler}) = {\rm Pr}({ \cal E} ) = {\rm Q} \left [ {d}/(2{\sigma_n}) \right ]\hspace{0.05cm}.$$

• Die mittlere Energie pro Symbol $(E_{\rm S})$ ergibt sich für die obere Konstellation zu

$$E_{\rm S} = 1/2 \cdot \vert \hspace{-0.05cm} \vert s_0 \vert \hspace{-0.05cm} \vert^2 + 1/2 \cdot \vert \hspace{-0.05cm} \vert s_1 \vert \hspace{-0.05cm} \vert^2 = E/2 \cdot [(+2)^2 + (-2)^2] = 4 \cdot {E}\hspace{0.05cm}.$$

• Bei der unteren Konstellation erhält man in gleicher Weise:

$$E_{\rm S} = \ \text{...} \ = E/2 \cdot [(3.6)^2 + (0.8)^2] + E/2 \cdot [(0.4)^2 + (3.2)^2] = 12 \cdot {E}\hspace{0.05cm}.$$

• Bei gegebener mittlerer Energie pro Symbol $(E_{\rm S})$ ist demnach ist die oberee Konstellation der un teren deutlich überlegen: Die gleiche Fehlerwahrscheinlichkeit ergibt sich mit einem Drittel der aufzuwendenden Energie pro Symbol. Auf diesen Sachverhalt wird in der Aufgabe 4.6Z noch im Detail eingegangen.

Optimale Schwelle bei nicht gleichwahrscheinlichen Symbolen

Gilt ${\rm Pr}(m_0) \ne {\rm Pr}(m_1)$, so kann man durch eine Verschiebung der Entscheidungsgrenze $G$ eine etwas kleinere Fehlerwahrscheinlichkeit erreichen. Die nachfolgenden Ergebnisse werden ausführlich in der Musterlösung zur Aufgabe 4.7 hergeleitet:

• Bei ungleichen Symbolwahrscheinlichkeiten liegt die optimale Entscheidungsgrenze $G_{\rm opt}$ zwischen den Regionen $I_0$ und $I_1$ näher beim unwahrscheinlicheren Symbol.
  

• Die normierte optimale Verschiebung gegenüber der Grenze $G = 0$ bei gleichwahrscheinlichen Symbolen beträgt

\[\gamma_{\rm opt} = \frac{G_{\rm opt}}{s_0 } = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} \hspace{0.05cm}.\]

• Die Fehlerwahrscheinlichkeit ist dann gleich

$${\rm Pr}({ \cal E} ) = {\rm Pr}(m_0) \cdot {\rm Q} \left[ {d}/(2{\sigma_n}) \cdot (1 - \gamma_{\rm opt}) \right ] + {\rm Pr}(m_1) \cdot {\rm Q} \left [ {d}/(2{\sigma_n}) \cdot (1 + \gamma_{\rm opt}) \right ]\hspace{0.05cm}.$$

$\text{Beispiel 2:}$  Für das Folgende gelte

$$\boldsymbol{ s }_0 = (2 \cdot \sqrt{E}, \hspace{0.1cm} 0), \hspace{0.2cm} \boldsymbol{ s }_1 = (- 2 \cdot \sqrt{E}, \hspace{0.1cm} 0), \hspace{0.2cm} \Rightarrow \hspace{0.2cm} d = 2 \cdot \sqrt{E}, \hspace{0.2cm} \sigma_n = \sqrt{E} \hspace{0.05cm}.$$

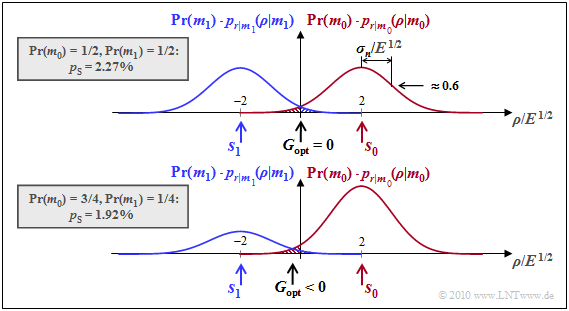
Bei gleichwahrscheinlichen Symbolen   ⇒   ${\rm Pr}( m_0) = {\rm Pr}( m_1) = 1/2$ ergibt sich die optimale Entscheidungsgrenze zu $G_{\rm opt} = 0$ (siehe obere Skizze). Damit erhält man für die Fehlerwahrscheinlichkeit:

$${\rm Pr}({ \cal E} ) = {\rm Q} \left [ {d}/(2{\sigma_n}) \right ] = {\rm Q} (2) \approx 2.26\% \hspace{0.05cm}.$$

Dichtefunktionen für gleiche/ungleiche Symbolwahrscheinlichkeiten

Nun betrachten wir mit ${\rm Pr}( m_0) = 3/4\hspace{0.05cm},\hspace{0.1cm}{\rm Pr}( m_1) = 1/4\hspace{0.05cm}$ ungleiche Symbolwahrscheinlichkeiten, wie für die untere Skizze vorausgesetzt. Die weiteren Systemgrößen seien gegenüber der oberen Grafik unverändert:

\[\boldsymbol{ s }_0 = (2 \cdot \sqrt{E}, \hspace{0.1cm} 0), \hspace{0.2cm} \boldsymbol{ s }_1 = (- 2 \cdot \sqrt{E}, \hspace{0.1cm} 0), \hspace{0.2cm} \Rightarrow \hspace{0.2cm} d = 2 \cdot \sqrt{E}, \hspace{0.2cm} \sigma_n = \sqrt{E} \hspace{0.05cm}.\]

In diesem Fall beträgt der optimale (normierte) Verschiebungsfaktor

\[\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}( m_1)}{ {\rm Pr}( m_0)} = 2 \cdot \frac{ E}{16 \cdot E} \cdot {\rm ln} \hspace{0.15cm} \frac{1/4}{3/4 } \approx - 0.14 \hspace{0.05cm},\]

was einer Verschiebung um $14\%$ hin zum unwahrscheinlicheren Symbol $\boldsymbol {s}_1$ (also nach links) bedeutet. Dadurch wird die Fehlerwahrscheinlichkeit geringfügig kleiner als bei gleichwahrscheinlichen Symbolen:

\[{\rm Pr}({ \cal E} )= 0.75 \cdot {\rm Q} \left ( 2 \cdot 1.14 \right ) + 0.25 \cdot {\rm Q} \left ( 2 \cdot 0.86 \right ) = 0.75 \cdot 0.0113 + 0.25 \cdot 0.0427 \approx 1.92\% \hspace{0.05cm}.\]

Man erkennt aus diesen Zahlenwerten:

• Durch die Schwellenverschiebung wird nun zwar das Symbol $\boldsymbol {s}_1$ stärker verfälscht, das wahrscheinlichere Symbol $\boldsymbol {s}_0$ jedoch überproportional weniger.
  

• Das Ergebnis sollte aber nicht zu Fehlinterpretationen führen. Im unsymmetrischen Fall  ⇒  ${\rm Pr}( m_0) \ne {\rm Pr}( m_1)$ ergibt sich zwar eine kleinere Fehlerwahrscheinlichkeit als für ${\rm Pr}( m_0) ={\rm Pr}( m_1) = 0.5$, aber mit jedem Symbol kann dann auch nur weniger Information übertragen werden, bei den gewählten Zahlenwerten $0.81 \ \rm bit/Symbol$ statt $1\ \rm bit/Symbol$.
• Aus informationstheoretischer Sicht ist ${\rm Pr}( m_0) ={\rm Pr}( m_1)$ optimal.

$\text{Fazit:}$  Während im symmetrischen Fall   ⇒   ${\rm Pr}( m_0) ={\rm Pr}( m_1)$ zur Entscheidungsfindung die herkömmlichen bedingten Wahrscheinlichkeitsdichtefunktionen $p_{r \hspace{0.02cm}\vert \hspace{0.02cm}m } ( \rho \hspace{0.05cm}\vert \hspace{0.05cm}m_i )$ herangezogen können, müssen bei   ${\rm Pr}( m_0) \ne {\rm Pr}( m_1)$ diese Funktionen vorher gewichtet werden:   ${\rm Pr}(m_i) \cdot p_{r \hspace{0.02cm}\vert \hspace{0.02cm}m_i } ( \rho \hspace{0.05cm}\vert \hspace{0.05cm}m_i )$. Der formale Parameter $\rho$ gibt dabei wieder eine Realisierung der AWGN–Zufallsgröße r = s + n an. Im Folgenden wird dieser Sachverhalt berücksichtigt.

Entscheidungsregionen im nichtbinären Fall

Allgemein partitionieren die Entscheidungsregionen $I_i$ den $N$–dimensionalen reellen Raum in $M$ zueinander disjunkte Gebiete. $I_i$ ist definiert als die Menge aller Punkte, die zum Schätzwert $m_i$ führen:

\[\boldsymbol{ \rho } \in I_i \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm} \hat{m} = m_i, \hspace{0.3cm}{\rm wobei}\hspace{0.3cm}I_i = \left \{ \boldsymbol{ \rho } \in { \cal R}^N \hspace{0.05cm} | \hspace{0.05cm} {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } |m_i ) > {\rm Pr}( m_k) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } |m_k )\hspace{0.15cm} \forall k \ne i \right \} \hspace{0.05cm}.\]

Die Form der Entscheidungsregionen $I_i$ mit $i = 0$, ... , $M-1$ im $N$&–dimensionalen Raum hängen von den bedingten Wahrscheinlichkeitsdichtefunktionen $p_{r \hspace{0.02cm}\vert \hspace{0.02cm}m }$ ab, also vom betrachteten Kanal. In vielen Fällen – so auch beim AWGN–Kanal – sind die Entscheidungsgrenzen zwischen je zwei Signalpunkten Gerade, was die weiteren Betrachtungen deutlich vereinfacht.

Entscheidungsregionen für AWGN, N = 2, M = 3

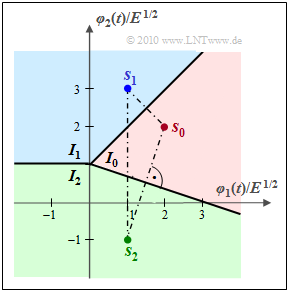
$\text{Beispiel 3:}$  Die Grafik zeigt die Entscheidungsregionen $I_0$, $I_1$ und $I_2$ für ein Übertragungssystem mit den Parametern $N = 2$ und $M = 3$.

Die normierten Sendevektoren sind dabei

\[\boldsymbol{ s }_0 = (2,\hspace{0.05cm} 2), \hspace{0.2cm} \hspace{0.01cm} \boldsymbol{ s }_1 = (1,\hspace{0.05cm} 3), \hspace{0.01cm} \hspace{0.2cm} \boldsymbol{ s }_2 = (1,\hspace{0.05cm} -1) \hspace{0.05cm}.\]

Es sind nun zwei Fälle zu unterscheiden:

• Bei gleichwahrscheinlichen Symbolen   ⇒   ${\rm Pr}( m_0) = {\rm Pr}( m_1) ={\rm Pr}( m_2) = 1/3 $ verlaufen die Grenzen zwischen jeweils zwei Regionen stets geradlinig, mittig und rechtwinklig zu den Verbindungsgeraden.
  

• Bei ungleichen Symbolwahrscheinlichkeiten sind die Entscheidungsgrenzen dagegen jeweils in Richtung des unwahrscheinlicheren Symbols (parallel) zu verschieben, und zwar umso weiter, je größer die AWGN–Streuung $\sigma_n$ ist.

Nachdem die Entscheidungsregionen $I_i$ festliegen, kann man die Symbolfehlerwahrscheinlichkeit des Gesamtsystems berechnen. Auf den nächsten Seiten benutzen wir folgende Bezeichnungen, wobei wir aufgrund der Einschränkungen durch den verwendeten Zeichensatz im Fließtext manchmal andere Namen als in Gleichungen verwenden müssen:

• Symbolfehlerwahrscheinlichkeit:   ${\rm Pr}({ \cal E} ) = {\rm Pr(Symbolfehler)} \hspace{0.05cm},$

• Wahrscheinlichkeit für eine korrekte Entscheidung:   ${\rm Pr}({ \cal C} ) = 1 - {\rm Pr}({ \cal E} ) = {\rm Pr(korrekte \hspace{0.15cm} Entscheidung)} \hspace{0.05cm},$

• Bedingte Wahrscheinlichkeit einer korrekten Entscheidung unter der Bedingung $m = m_i$:   ${\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = 1 - {\rm Pr}({ \cal E} \hspace{0.05cm}|\hspace{0.05cm} m_i) \hspace{0.05cm}.$

Fehlerwahrscheinlichkeitsberechnung im nichtbinären Fall

Mit den Definitionen der letzten Seite gilt für die Wahrscheinlichkeit einer korrekten Entscheidung:

\[{\rm Pr}({ \cal C} ) \hspace{-0.1cm} = \hspace{-0.1cm} \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot \int_{I_i} p_{{ \boldsymbol{ r }} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol {\rho } \hspace{0.05cm}|\hspace{0.05cm} m_i ) \,{\rm d} \boldsymbol {\rho } \hspace{0.05cm}.\]

Für den AWGN–Kanal gilt dabei entsprechend dem Abschnitt N–dimensionales Gaußsches Rauschen:

\[{\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = 1 - {\rm Pr}({ \cal E} \hspace{0.05cm}|\hspace{0.05cm} m_i) = \frac{1}{(\sqrt{2\pi} \cdot \sigma_n)^N} \cdot \int_{I_i} {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot || \boldsymbol{ \rho } - \boldsymbol{ s }_i ||^2 \right ] \,{\rm d} \boldsymbol {\rho }\hspace{0.05cm}.\]

Dieses Integral muss im allgemeinen Fall numerisch berechnet werden. Nur bei einigen wenigen, einfach beschreibbaren Entscheidungsregionen $\{I_i\}$ ist eine analytische Lösung möglich.

$\text{Beispiel 4:}$  Beim AWGN–Kanal liegt eine 2D–Gaußglocke um den Sendepunkt $\boldsymbol{ s }_i$, in der linken Grafik erkennbar an den konzentrischen Höhenlinien. Etwas willkürlich ist zudem die Entscheidungsgerade $G$ eingezeichnet. Rechts dargestellt ist in einem anderen Koordinatensystem (verschoben und gedreht) allein die WDF der Rauschkomponente.

Zur Berechnung der Fehlerwahrscheinlichkeit bei AWGN

Die Grafik lässt sich wie folgt interpretieren:

• Die Wahrscheinlichkeit, dass der Empfangsvektor nicht in das Gebiet $I_i$ fällt, sondern in das rot hinterlegte Gebiet $I_k$, ist $ {\rm Q} (A/\sigma_n)$. $A$ ist der Abstand zwischen $\boldsymbol{ s }_i$ und $G$. Der Effektivwert (Wurzel aus der Varianz) des AWGN–Rauschens ist mit $\sigma_n$ bezeichnet. ${\rm Q}(x)$ ist die Gaußsche Fehlerfunktion.
  

• Entsprechend ist die Wahrscheinlichkeit für das Ereignis $r \in I_i$ gleich dem Komplementärwert

\[{\rm Pr}({ \cal C}\hspace{0.05cm}\vert\hspace{0.05cm} m_i ) = {\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm} \vert \hspace{0.05cm} m_i ) = 1 - {\rm Q} (A/\sigma_n)\hspace{0.05cm}.\]

Wir betrachten nun die auf der letzten Seite angegebenen Gleichungen

\[{\rm Pr}({ \cal C} ) = \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{0.3cm}{\rm mit} \hspace{0.3cm} {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \int_{I_i} p_{{ \boldsymbol{ r }} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol {\rho } \hspace{0.05cm}|\hspace{0.05cm} m_i ) \,{\rm d} \boldsymbol {\rho } \hspace{0.05cm}\]

etwas genauer, wobei wir wieder von zwei Basisfunktionen $(N = 2)$ und den drei Signalraumpunkten $\boldsymbol{ s }_0$, $\boldsymbol{ s }_1$ und $\boldsymbol{ s }_2$ $(M = 3)$ ausgehen.

• Die Entscheidungsregionen $I_0$, $I_1$ und $I_2$ sind bestmöglich gewählt.
• Das AWGN–Rauschen ist in der Skizze durch jeweils drei kreisförmige Höhenlinien angedeutet.

Fehlerwahrscheinlichkeitsberechnung beim AWGN-Kanal und M = 3

Man erkennt aus dieser Darstellung:

• Unter der Voraussetzung, dass $m = m_i \ \Leftrightarrow \ \boldsymbol{ s } = \boldsymbol{ s }_i$ gesendet wurde, wird nur dann eine richtige Entscheidung getroffen, wenn der Empfangswert $\boldsymbol{ r }$ in der Region $I_i$ liegt.
  

• Die Wahrscheinlichkeit ${\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm}|\hspace{0.05cm}m_2)$ für eine ist für $i = 2$ (weitaus) am größten   ⇒   richtige Entscheidung. ${\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm}m_2)$ ist deutlich kleiner. Nahezu vernachlässigbar ist ${\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm}m_2)$.

• Die Verfälschungswahrscheinlichkeiten für $m = m_0$ bzw. $m = m_1$ lauten:

\[{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 )={\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm} m_0 ) + {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_0 ),\]

\[ {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 ) ={\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm} m_1 ) + {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_1 ) \hspace{0.05cm}.\]

• Die größte Verfälschungswahrscheinlichkeit ergibt sich für $m = m_0$. Wegen

\[{\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm} m_0 ) \approx {\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm} m_1 ) \hspace{0.05cm}, \]

\[{\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_0 ) \gg {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_1 ) \hspace{0.05cm}\]

gelten folgende Relationen:   ${\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 ) > {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 ) >{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_2 )\hspace{0.05cm}. $

$\text{Fazit:}$  Diese Ergebnisse lassen sich wie folgt zusammenfassen:

• Zur Berechnung der (mittleren) Fehlerwahrscheinlichkeit muss auch bei gleichwahrscheinlichen Symbolen allgemein über alle $M$ Terme gemittelt werden. Ausnahme: Symmetrische Anordnung.
  

• Im Fall gleichwahrscheinlicher Symbole kann ${\rm Pr}(m_i) = 1/M$ vor die Summation gezogen werden, was allerdings den Rechengang nicht sonderlich vereinfacht.

Union Bound - Obere Schranke für die Fehlerwahrscheinlichkeit

Bei beliebigen Werten von $M$ gilt für die Verfälschungswahrscheinlichkeit unter der Voraussetzung, dass die Nachricht $m_i$ (bzw. das Signal $\boldsymbol{s}_i$ gesendet wurde:

\[{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = {\rm Pr} \left [ \bigcup_{k \ne i} { \cal E}_{ik}\right ] \hspace{0.05cm},\hspace{0.2cm}{ \cal E}_{ik}\hspace{-0.1cm}: \boldsymbol{ r }{\rm \hspace{0.15cm}liegt \hspace{0.15cm}n\ddot{a}her \hspace{0.15cm}bei \hspace{0.15cm}}\boldsymbol{ s }_k {\rm \hspace{0.15cm}als \hspace{0.15cm}beim \hspace{0.15cm}Sollwert \hspace{0.15cm}}\boldsymbol{ s }_i \hspace{0.05cm}. \]

$\text{Definition:}$  Für diesen Ausdruck lässt sich mit einer Booleschen Ungleichung, der so genannten Union Bound, eine obere Schranke angeben:

\[{\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_i ) \le \sum\limits_{k = 0, \hspace{0.1cm}k \ne i}^{M-1} {\rm Pr}({ \cal E}_{ik}) = \sum\limits_{k = 0, \hspace{0.1cm}k \ne i}^{M-1}{\rm Q} \left [ d_{ik}/(2{\sigma_n}) \right ]\hspace{0.05cm}. \]

Anmerkungen:

• Es ist $d_{ik} = \vert \hspace{-0.05cm} \vert \boldsymbol{s}_i - \boldsymbol{s}_k \vert \hspace{-0.05cm} \vert$ der Abstand der Signalraumpunkte $\boldsymbol{s}_i$ und $\boldsymbol{s}_k$; $\sigma_n$ gibt den Effektivwert des AWGN–Rauschens an.
  

• Die Union Bound ist nur bei gleichwahrscheinlichen Symbolen   ⇒   ${\rm Pr}(m_i) = 1/M$ anwendbar. Auch dann muss zur Berechnung der (mittleren) Fehlerwahrscheinlichkeit über alle $m_i$ gemittelt werden.

$\text{Beispiel 5:}$  Die Grafik verdeutlicht die Union Bound am Beispiel $M = 3$ mit gleichwahrscheinlichen Symbolen: ${\rm Pr}(m_0) = {\rm Pr}(m_1) = {\rm Pr}(m_2) =1/3$.

Zur Verdeutlichung der „Union Bound”

Zu diesen Darstellungen ist anzumerken:

• Für die Symbolfehlerwahrscheinlichkeit gilt:

\[{\rm Pr}({ \cal E} ) = 1 - {\rm Pr}({ \cal C} ) \hspace{0.05cm},\hspace{0.2cm}{\rm Pr}({ \cal C} ) = {1}/{3} \cdot \left [ {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_0 ) + {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_1 ) + {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_2 ) \right ]\hspace{0.05cm}.\]

• Der erste Term im Klammerausdruck unter der Voraussetzung $m = m_0 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_0$ ist in der linken Grafik visualisiert. Dieser Term ${\rm Pr}(\boldsymbol{r} \in I_0\hspace{0.05cm}\vert \hspace{0.05cm} m_0)$ beschreibt die rot ausgefüllte Region $I_0$.
  

• Die Komplementärregion ${\rm Pr}(\boldsymbol{r} \not\in I_0\hspace{0.05cm}\vert \hspace{0.05cm} m_0)$ ist in der linken Grafik entweder blau oder grün oder blau–grün schraffiert markiert. Es gilt ${\rm Pr}({ \cal C}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) = 1 - {\rm Pr}({ \cal E}\hspace{0.05cm}\vert \hspace{0.05cm} m_0 )$ mit

$${\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) = {\rm Pr}(\boldsymbol{ r } \in I_1 \hspace{0.05cm}\cup \hspace{0.05cm} \boldsymbol{ r } \in I_2 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) \le {\rm Pr}(\boldsymbol{ r } \in I_1 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) + {\rm Pr}(\boldsymbol{ r } \in I_2 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) ={\rm Q} \left [ d_{01}/(2{\sigma_n}) \right ]+ {\rm Q} \left [ d_{02}/(2{\sigma_n}) \right ] \hspace{0.05cm}.$$

• Das „$\le$”–Zeichen berücksichtigt hier, dass die blau–grün schraffierte Fläche sowohl zum Gebiet „$\boldsymbol{r} \in I_1$” als auch zum Gebiet „$\boldsymbol{r} \in I_2$” gehört, so dass die Summe einen zu großen Wert liefert. Das heißt: Die Union Bound liefert stets eine obere Schranke.
  

• Die mittlere Grafik verdeutlicht die Berechnung der Union Bound unter der Voraussetzung, dass $m = m_1 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_1$ gesendet wurde. Für das rechte Bild ist $m = m_2 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_2$ zugrundegelegt.

Weitere Aufwandsreduzierung bei der Union Bound

Zur Verdeutlichung der Nachbarmengen N(i)

Die Abschätzung nach der „Union Bound” lässt sich verbessern, indem man nur solche Signalraumpunkte berücksichtigt, die direkte Nachbarn des aktuellen Sendevektors $\boldsymbol{s}_i$ sind:

\[{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{k = 0, \hspace{0.1cm} k \ne i}^{M-1}{\rm Q}\left [ d_{ik}/(2{\sigma_n}) \right ] \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{k = 0, \hspace{0.1cm} k \hspace{0.05cm}\in \hspace{0.05cm}N(i)}^{M-1}\hspace{-0.4cm}{\rm Q} \left [ d_{ik}/(2{\sigma_n}) \right ] \hspace{0.05cm}. \]

Dazu definieren wir die Nachbarn von $\boldsymbol{s}_i$ als

\[N(i) = \left \{ k \in \left \{ i = 0, 1, 2, ... \hspace{0.05cm}, M-1 \right \}\hspace{0.05cm}|\hspace{0.05cm} I_i {\rm \hspace{0.15cm}grenzt \hspace{0.15cm}direkt \hspace{0.15cm}an \hspace{0.15cm}}I_k \right \} \hspace{0.05cm}. \]

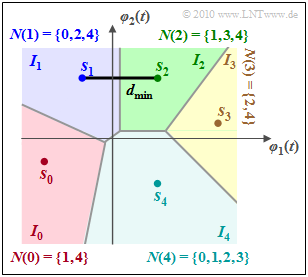
Die Grafik verdeutlicht diese Definiton am Beispiel $M = 5$. Die Regionen $I_0$ und $I_3$ haben jeweils nur zwei direkte Nachbarn, während $I_4$ an alle anderen Entscheidungsregionen angrenzt.

Durch die Einführung der Nachbarmengen $N(i)$ wird die Qualität der Union Bound–Approximation verbessert, das heißt, die Schranke liegt dann näher an der tatsächlichen Fehlerwahrscheinlichkeit, wird also nach unten verschoben.

Eine weitere und häufig verwendete Schranke benutzt nur den minimalen Abstand $d_{\rm min}$ zwischen zwei Signalpunkten. Im obigen Beispiel tritt dieser zwischen $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ auf. Dann gilt für gleichwahrscheinliche Symbole   ⇒   ${\rm Pr}(m_i) =1/M$ die folgende Abschätzung:

\[{\rm Pr}({ \cal E} ) \le \sum\limits_{i = 0 }^{M-1} \big [ {\rm Pr}(m_i) \cdot \sum\limits_{k \ne i }{\rm Q} [d_{ik}/(2{\sigma_n})] big ] \le \frac{1}{M} \cdot \sum\limits_{i = 0 }^{M-1} \left [ \sum\limits_{k \ne i } {\rm Q} [d_{\rm min}/(2{\sigma_n})] \right ] = \sum\limits_{k \ne i }{\rm Q} [d_{\rm min}/(2{\sigma_n})] = (M-1) \cdot {\rm Q} [d_{\rm min}/(2{\sigma_n})] \hspace{0.05cm}. \]

Hierzu ist anzumerken:

• Diese Schranke ist auch für große $M$–Werte sehr einfach zu berechnen. Bei vielen Anwendungen ergibt sich jedoch damit ein viel zu großer Wert für die Fehlerwahrscheinlichkeit.
  

• Die Schranke ist nur dann gleich der tatsächlichen Fehlerwahrscheinlichkeit, wenn alle Regionen an alle anderen direkt angrenzen und die Distanzen aller $M$ Signalpunkte zueinander gleich $d_{\rm min}$ sind.
  

• Im Sonderfall $M = 2$ sind diese beiden Voraussetzungen häufig erfüllt, so dass dann die hier angegebene Schranke exakt mit der tatsächlichen Fehlerwahrscheinlichkeit übereinstimmt.
  

Aufgaben zum Kapitel

A4.6 Optimale Entscheidungsgrenze

Zusatzaufgaben:4.6 Signalraumkonstellationen

4.7 Nochmals Entscheidungsgrenzen

A4.8 Entscheidungsregionen

Zusatzaufgaben:4.8 Fehlerwahrscheinlichkeit

A4.9 Entscheidungsregionen bei Laplace

Zusatzaufgaben:4.9 Laplace-verteiltes Rauschen

[Union Bound]