Aufgabe 1.2: Einfacher binärer Kanalcode

• Zurück zum Buch

Zur Verdeutlichung der Kanalcodierung

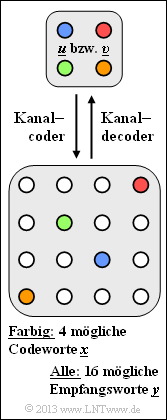
Die Grafik verdeutlicht die hier betrachtete Kanalcodierung $\mathcal{C}$:

• Es gibt vier mögliche Informationsblöcke $\underline{u} = (u_{1}, u_{2}, \text{...}\hspace{0.05cm} , u_{k})$.
• Jeder Informationsblock $\underline{u}$ wird eindeutig (erkennbar an der gleichen Farbe) dem Codewort $\underline{x}= (x_{1}, x_{2}, \text{...}\hspace{0.05cm} , x_{n})$ zugeordnet.
• Aufgrund von Decodierfehlern $(0 → 1, \ 1 → 0)$ gibt es mehr als 4, nämlich 16 verschiedene Empfangsworte $\underline{y} = (y_{1}, y_{2}, \text{...} \hspace{0.05cm} , y_{n})$.

Ab Teilaufgabe (4) betrachten wir folgende Zuordnung:

$$\underline{u_0} = (0, 0) \leftrightarrow (0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm},$$

$$\underline{u_1} = (0, 1) \leftrightarrow (0, 1, 0, 1) = \underline{x_1}\hspace{0.05cm},$$

$$\underline{u_2} = (1, 0) \leftrightarrow (1, 0, 1, 0) = \underline{x_2}\hspace{0.05cm},$$

$$\underline{u_3} = (1, 1) \leftrightarrow (1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Zielsetzung der Kanalcodierung
• Bezug genommen wird insbesondere auf die Seiten Blockschaltbild und Voraussetzungen und Einige wichtige Definitionen zur Blockcodierung.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Aus wievielen Binärsymbolen besteht ein Informationsblock?

$k \ = \ $

2

Wie groß ist die Codewortlänge $n$?

$n \ = \ $

3

Wie groß ist die Coderate?

$R \ = \ $

4

Ist der hier vorgegebene Code systematisch?

	Ja,
	Nein.

5

Geben Sie die Hamming–Gewichte aller Codeworte an.

$ w_{\rm H} \ (\underline{x}_0) \ = \ $

$ w_{\rm H} \ (\underline{x}_1) \ = \ $

$ w_{\rm H} \ (\underline{x}_2) \ = \ $

$ w_{\rm H} \ (\underline{x}_3) \ = \ $

6

Geben Sie die Hamming–Distanzen zwischen folgenden Codeworten an.

$ d_{\rm H} \ (\underline{x}_0, \underline{x}_1) \ = \ $

$ d_{\rm H} \ (\underline{x}_0, \underline{x}_3) \ = \ $

$ d_{\rm H} \ (\underline{x}_1, \underline{x}_2) \ = \ $

7

Wie groß ist die minimale Hamming–Distanz des betrachteten Codes $\mathcal{C}$?

$ d_{\rm min} \ (\mathcal{C}) \ = \ $

Musterlösung

Musterlösung

(1)  Der Codeumfang ist hier zu |C| = 4 gegeben. Allgemein gilt |C| = $2^k$. Daraus folgt $\underline{ k = 2}$.

(2)  Jedes Codewort x ist eineindeutig einem Informationsblock u zugeordnet. Durch Verfälschungen einzelner der insgesamt n Bit eines Codewortes x ergeben sich die Empfangsworte y . Aus der Anzahl (16 = $2^4$) der möglichen Empfangsworte folgt $\underline{ n = 4}$.

(3)  Die Coderate ist per Definition R = k/n. Mit den obigen Ergebnissen erhält man R = 1/2.

(4)  Richtig ist Ja. Ein systematischer Code zeichnet sich dadurch aus, dass jeweils die ersten k Bit der Codeworte identisch sind mit dem Informationsblock.

(5)  Das Hamming–Gewicht eines binären Codes ist gleich der algebraischen Summe x_1 + x_2 + ... + x_n über alle Codewortelemente. Damit gilt:

$$w_{\rm H}(\underline{x}_0) \hspace{0.15cm} \underline {= 0} \hspace{0.05cm}, \hspace{0.3cm}w_{\rm H}(\underline{x}_1) \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}, \hspace{0.3cm} w_{\rm H}(\underline{x}_2) \hspace{0.15cm} \underline {= 2}\hspace{0.05cm}, \hspace{0.3cm}w_{\rm H}(\underline{x}_3) \hspace{0.15cm} \underline {= 4}\hspace{0.05cm}.$$

(6)  Die Hamming–Distanz zwischen zwei Codeworten kann hier nur die Werte 2 und 4 annehmen:

$$d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_1) \hspace{0.15cm} \underline {= 2}\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_2) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_3) \hspace{0.15cm} \underline {= 4}\hspace{0.05cm},$$

$$ d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_2) \hspace{0.15cm} \underline {= 4}\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_3) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_2, \hspace{0.05cm}\underline{x}_3) = 2\hspace{0.05cm}.$$

(6)  Aus dem Ergebnis der Teilaufgabe 6 folgt d_{\rm min}(C) = 2. Allgemein gilt für diese Größe:

$$d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}')\hspace{0.05cm}.$$