Aufgabe 3.5: PM und FM bei Rechtecksignalen

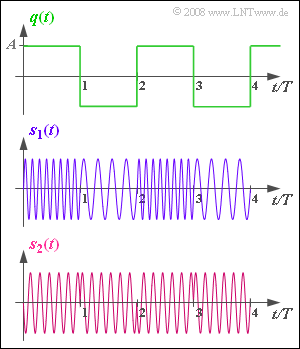
Zwei Signalverläufe bei Winkelmodulation

Wir gehen von einem bipolaren und rechteckförmigen Quellensignal $q(t)$ aus, wie im oberen Diagramm dargestellt. Dieses Signal kann nur die beiden Signalwerte $±A = ±2 \ \rm V$ annehmen und die Dauer der positiven und negativen Rechtecke ist jeweils $T = 1 \ \rm ms$. Die Periodendauer von $q(t)$ ist demzufolge $T_0 = 2 \ \rm ms$.

Die Signale $s_1(t)$ und $s_2(t)$ zeigen zwei Sendesignale bei Winkelmodulation (WM), die jeweils in der Form

$$s(t) = A_{\rm T} \cdot \cos \hspace{-0.05cm}\big [\psi (t) \big ]$$

darstellbar sind. Hierbei unterscheidet man zwischen der Phasenmodulation (PM) mit der Winkelfunktion

$$\psi(t) = \omega_{\rm T} \cdot t + \phi(t) = \omega_{\rm T} \cdot t + K_{\rm PM} \cdot q(t)$$

und der Frequenzmodulation (FM), bei der die Augenblicksfrequenz linear mit $q(t)$ zusammenhängt:

$$f_{\rm A}(t) = \frac{\omega_{\rm A}(t)}{2\pi}, \hspace{0.3cm} \omega_{\rm A}(t) = \frac{{\rm d}\hspace{0.03cm}\psi(t)}{{\rm d}t}= \omega_{\rm T} + K_{\rm FM} \cdot q(t)\hspace{0.05cm}.$$

$K_{\rm PM}$ und $K_{\rm FM}$ bezeichnen dimensionsbehaftete, durch die Realisierung des PM– bzw. FM–Modulators vorgegebene Konstante. Der Frequenzhub $Δf_{\rm A}$ gibt die maximale Abweichung der Augenblicksfrequenz von der Trägerfrequenz an.

Hinweise:

Die Aufgabe gehört zum Kapitel Frequenzmodulation.
Bezug genommen wird aber auch auf das Kapitel Phasenmodulation.

Im Vorgriff auf das vierte Kapitel sei erwähnt, dass man die Phasenmodulation bei digitalem Eingangssignal auch als Phase Shift Keying (PSK) und entsprechend die Frequenzmodulation als Frequency Shift Keying (FSK) bezeichnet.

Fragebogen

	$s_1(t)$ beschreibt eine Phasenmodulation.
	$s_1(t)$ beschreibt eine Frequenzmodulation.

$ϕ_{\rm T} \ = \ $

$\ \rm Grad$

$f_{\rm T} · T \ = \ $

$K_{\rm PM} \ = \ $

$\ \rm V^{-1}$

$Δf_{\rm A} · T \ = \ $

$K_{\rm FM} \ = \ $

$\ \rm (Vs)^{-1}$

Musterlösung

(1) Richtig ist die Antwort 2:

Bei einem rechteckförmigen (digitalen) Quellensignal erkennt man die Phasenmodulation (PM) an den typischen Phasensprüngen – siehe Signalverlauf $s_2(t)$.
Die Frequenzmodulation (FM) hat dagegen zu den verschiedenen Zeiten unterschiedliche Augenblicksfrequenzen wie bei $s_1(t)$.

(2) Mit $q(t) = 0$ erhält man entsprechend den gegebenen Gleichungen sowohl für PM als auch für FM

$$s(t) = A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t ) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \phi_{\rm T} \hspace{0.15cm}\underline {= 0}\hspace{0.05cm}.$$

(3) Die Trägerfrequenz $f_{\rm T}$ kann direkt nur aus dem PM–Signal $s_2(t)$ ermittelt werden.

Durch Abzählen der Schwingungen von $s_2(t)$ im Zeitintervall $T$ erkennt man, dass $f_{\rm T} · T\hspace{0.15cm}\underline{ = 6}$ verwendet wurde.
Bei der Frequenzmodulation eines bipolaren Quellensignals tritt $f_{\rm T}$ nicht direkt auf. Die Grafiken lassen allerdings darauf schließen, dass hier ebenfalls $f_{\rm T} · T = 6$ zugrunde liegt.

(4) Der Amplitudenwert $A = 2 \ \rm V$ führt zur Phase $90^\circ$ bzw. $π/2$ (Minus–Sinusverlauf). Daraus folgt:

$$K_{\rm PM} = \frac {\pi /2}{2\,{\rm V}} \hspace{0.15cm}\underline {= 0.785\,{\rm V}^{-1}} \hspace{0.05cm}.$$

(5) Die Grafik für $s_1(t)$ zeigt, dass innerhalb eines Zeitintervalls $T$ entweder vier oder acht Schwingungen auftreten: $4 \le f_{\rm A}(t) \cdot T \le 8\hspace{0.05cm}.$ Unter Berücksichtigung der (normiertern) Trägerfrequenz $f_{\rm T} · T = 6$ ergibt sich für den (normierten) Frequenzhub:

$$\Delta f_{\rm A} \cdot T \hspace{0.15cm}\underline {=2}\hspace{0.05cm}.$$

(6) Der Frequenzhub kann auch wie folgt dargestellt werden: $$\Delta f_{\rm A} = \frac {K_{\rm FM}}{2\pi}\cdot A \hspace{0.05cm}.$$ Mit $Δf_A · {\rm A} = 2$ erhält man somit

$$K_{\rm FM} = \frac {2 \cdot 2\pi}{A \cdot T}= \frac {4\pi}{2\,{\rm V} \cdot 1\,{\rm ms}}\hspace{0.15cm}\underline {= 6283 \,{\rm V}^{-1}{\rm s}^{-1}} \hspace{0.05cm}.$$