Einige systemtheoretische Tiefpassfunktionen
Inhaltsverzeichnis
Allgemeine Bemerkungen
Alle auf den nächsten Seiten beschriebenen Tiefpassfunktionen weisen die folgenden Eigenschaften auf:
- Der Frequenzgang $H(f)$ ist reell und gerade, so dass nach dem Zuordnungssatz auch die zugehörige Impulsantwort $h(t)$ stets reell und gerade ist.
- Damit ist offensichtlich, dass die hier betrachteten Systeme akausal und somit nicht realisierbar sind. Die Beschreibung kausaler Systeme erfolgt im Kapitel Beschreibung kausaler realisierbarer Systeme dieses Buches.
- Der Vorteil dieser systemtheoretischen Filterfunktionen ist die einfache Beschreibung durch maximal zwei Parameter, so dass der Filtereinfluss durchschaubar dargestellt werden kann.
- Der wichtigste Funktionsparameter ist die äquivalente Bandbreite entsprechend der Definition über das flächengleiche Rechteck:
- $$\Delta f = \frac{1}{H(f=0)}\cdot \int_{-\infty}^{+\infty}H(f) \hspace{0.15cm} {\rm d}f.$$
- Nach dem so genannten Reziprozitätsgesetz liegt somit auch die äquivalente Zeitdauer der Impulsantwort fest, die ebenfalls über das flächengleiche Rechteck definiert ist:
- $$\Delta t = \frac{1}{h(t=0)}\cdot \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm} {\rm d}t = \frac{1}{\Delta f}.$$
- Der Gleichsignalübertragungsfaktor wird – wenn nicht explizit etwas Anderes vermerkt ist – stets zu $H(f = 0) = 1$ angenommen.
- Aus jeder Tiefpassfunktion lassen sich entsprechende Hochpassfunktionen ableiten, wie auf der Seite Herleitung systemtheoretischer Hochpassfunktionen gezeigt wird.
Idealer Tiefpass – Küpfmüller–Tiefpass
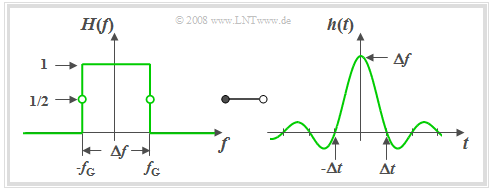
$\text{Definition:}$ Ein idealer Tiefpass liegt vor, wenn sein Frequenzgang wie folgt lautet:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ 0.5 \\\hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad\begin{array}{*{10}c} \text {für} \\ \text {für} \\ \text {für} \\ \end{array}\begin{array}{*{20}c}{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert< \Delta f/2,} \\{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert = \Delta f/2,} \\{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert > \Delta f/2.} \\\end{array}$$
Wir verwenden teilweise auch die Bezeichnung „Küpfmüller-Tiefpass” (KTP) in Erinnerung an den Pionier der Systemtheorie, Karl Küpfmüller.
Die Grafik zeigt einen solchen idealen Tiefpass im Frequenz– und Zeitbereich. Man erkennt aus diesem Kurvenverläufen:
- Aufgrund des abrupten, unendlich steilen Flankenabfalls ist hier die 3dB–Grenzfrequenz $f_{\rm G}$ genau halb so groß wie die systemtheoretische Bandbreite $Δf$.
- Alle Spektralanteile mit $f \lt f_{\rm G}$ werden unverfälscht durchgelassen (Durchlassbereich).
- Alle Anteile mit $f \gt f_{\rm G}$ werden vollständig unterdrückt (Sperrbereich).
- Bei $f = f_{\rm G}$ gilt definitionsgemäß $H(f) = 0.5$.
Beschreibung des idealen Tiefpasses im Zeitbereich:
- Die Impulsantwort (siehe rechte Grafik) ergibt sich entsprechend der Fourierrücktransformation zu
- $$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t)\hspace{0.7cm}{\rm{mit}}\hspace{0.7cm}{\rm si}(x) ={\sin(x)}/{x}.$$
- Die beidseitig bis ins Unendliche ausgedehnte Impulsantwort $h(t)$ weist äquidistante Nulldurchgänge im Abstand $Δt = 1/ Δf$ auf.
- Der asymptotische Abfall erfolgt umgekehrt proportional mit der Zeit:
- $$|h(t)| = \frac{\Delta f}{\pi \cdot \Delta f \cdot |t|} \cdot \left |{\rm sin}(\pi \cdot \Delta f\cdot t )\right | \le \frac{1}{\pi \cdot |t|}.$$
- Daraus folgt, dass die Impulsantwort erst für Zeiten $t \gt t_{1‰} = 318 \cdot \Delta t$ mit Sicherheit kleiner als $1‰$ des Impulsmaximums ist.
- Die Sprungantwort $\sigma(t)$ ergibt sich aus der Impulsantwort durch Integration und lautet:
- $${\sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau = \frac{1}{2} + \frac{1}{\pi} \cdot {\rm Si}(\pi \cdot\Delta f \cdot t ).$$
- Hierbei ist die so genannte Integral–Sinusfunktion verwendet:
- $${\rm Si}(x) = \int_{ 0 }^{ x } {{\rm si} ( \xi )} \hspace{0.1cm}{\rm d}\xi = x - \frac{x^3}{3 \cdot 3!} + \frac{x^5}{5 \cdot 5!} - \frac{x^7}{7 \cdot 7!}+\text{ ...}$$
- Diese besitzt folgende Eigenschaften:
- $${\rm Si}(0) = 0, \hspace{0.3cm}{\rm Si}(\infty) = \frac{\pi}{2}, \hspace{0.3cm}{\rm Si}(-x) = -{\rm Si}(x).$$
Hinweis: In manchen Büchern wird statt der Funktion ${\rm si}(x)$ die ähnliche Funktion ${\rm sinc}(x)$ verwendet:
- $${\rm si}(x) = \frac{\sin(x)}{x}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}{\rm sinc}(x) = \frac{\sin(\pi x)}{\pi x} = {\rm si}(\pi x).$$
Damit lautet die Impulsantwort des idealen Tiefpasses: $h(t)$ = $Δf · {\rm sinc}(Δf · t).$
Spalt–Tiefpass
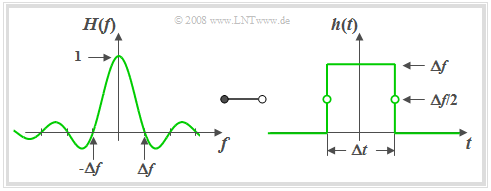
$\text{Definition:}$ Man bezeichnet ein LZI–System als Spalt–Tiefpass, wenn der Frequenzgang die folgende Form hat:
- $$H(f) = {\rm si}(\pi {f}/{ \Delta f})\hspace{0.7cm}{\rm{mit} }\hspace{0.7cm}{\rm si}(x) ={\sin(x)}/{x}.$$
Aus der linken Grafik ist zu erkennen, dass der Frequenzgang $H_{\rm STP}(f)$ des Spalt–Tiefpasses formgleich mit der Impulsantwort $h_{\rm KTP}(t)$ des Küpfmüllertiefpasses ist.
Nach dem Vertauschungssatz muss deshalb auch die Impulsantwort $h_{\rm STP}(t)$ des Spalt–Tiefpasses die gleiche Form wie der Frequenzgang $H_{\rm KTP}(f)$ des idealen Tiefpasses aufweisen.
Mit $Δt = 1/ Δf$ gilt somit:
- $$h(t) = \left\{ \begin{array}{l} \hspace{0.25cm}\Delta f \\ \Delta f/2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{für} \\ \text{für} \\ \text{für} \\ \end{array}\begin{array}{*{20}c} {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert < \Delta t/2,} \\ {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert = \Delta t/2,} \\ {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert > \Delta t/2.} \\ \end{array}$$
Anhand der rechten Grafik sind folgende Aussagen ableitbar:
- Auch der Spalt–Tiefpass ist in dieser Form akausal.
- Durch eine zusätzliche Laufzeit von $Δt/2$ wird das System jedoch kausal und damit realisierbar.
- Der Spalt–Tiefpass wirkt als Integrator über die Zeitdauer $Δt$:
- $$y(t) = x (t) * h (t) = \frac{1}{\Delta t} \cdot \int\limits_{ t - \Delta t/2 }^{ t + \Delta t/2 } {x ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$
- Ist $x(t)$ eine harmonische Schwingung mit der Frequenz $f_0 = k \cdot Δf$ (wobei $k$ ganzzahlig ist), so wird genau über $k$ Perioden integriert und es gilt $y(t) = 0$. Dies zeigen auch die Nullstellen von $H(f)$.
Gauß–Tiefpass
Eine häufig für systemtheoretische Untersuchungen verwendete Filterfunktion ist der Gaußtiefpass, der ebenfalls durch nur einen Parameter, nämlich die äquivalente Bandbreite $Δf$, beschreibbar ist.
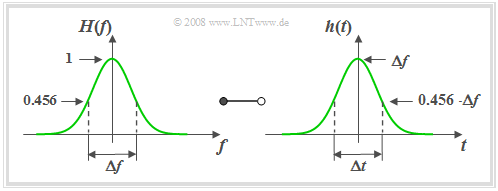
$\text{Definition:}$ Für den Frequenzgang und die Impulsantwort des Gaußtiefpasses gelten:
- $$H(f) = {\rm e}^{-\pi(f/\Delta f)^2}\hspace{0.15cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.15cm}h(t) = \Delta f \cdot {\rm e}^{-\pi(\Delta f \cdot \hspace{0.03cm} t)^2} .$$
Der Name geht auf den Mathematiker, Physiker und Astronomen Carl-Friedrich Gauß zurück. Gauß hat sich zwar nicht selber mit dieser Thematik auseinandergesetzt, aber die mathematische Form von Frequenzgang und Impulsantwort weisen eine Ähnlichkeit mit der so genannten Gaußformel auf, die er für die Wahrscheinlichkeitsrechnung gefunden hat.
Anhand dieser Grafik können folgende Aussagen getroffen werden:
- Die ebenfalls über das flächengleiche Rechteck definierte äquivalente Impulsdauer $Δt$ ist gleich dem Kehrwert der äquivalenten Bandbreite $Δf$.
- Eine schmalbandige Filterfunktion (kleines $Δf$) führt zu einer breiten (großes $Δt$) und gleichzeitig niedrigen Impulsantwort $h(t)$.
- Das so genannte Reziprozitätsgesetz von Zeitdauer und Bandbreite lässt sich am Beispiel des Gaußtiefpasses besonders anschaulich zeigen.
- Die Frequenz– und Zeitbereichsdarstellungen sind prinzipiell von gleicher Form. Man sagt auch, dass die Gaußfunktion invariant gegenüber der Fouriertransformation ist.
- Aufgrund der unendlichen Ausbreitung seiner Impulsantwort ist der Gaußtiefpass ebenso wie der ideale Tiefpass stark akausal und (exakt) nur mit unendlich großer Laufzeit realisierbar.
- Allerdings ist zu berücksichtigen, dass $h(t)$ bereits bei $t = 1.5 \cdot Δt$ auf $1‰$ seines Maximalwertes abgeklungen ist. Für $t = 3 \cdot Δt$ ergibt sich sogar $h(t) ≈ 5 · 10^{–13} · h(0)$.
- Diese Zahlenwerte machen deutlich, dass man den Gaußtiefpass durchaus auch für praxisnahe Simulationen heranziehen kann, solange Laufzeiten keine systembegrenzende Rolle spielen.
- Die Sprungantwort $σ(t)$ lautet mit der Gaußschen Fehlerfunktion $ϕ(x)$, die in Formelsammlungen meist tabellarisch angegeben wird:
- $$\sigma(t) = \int_{ -\infty }^{ t } {h(\tau)} \hspace{0.1cm}{\rm d}\tau = {\rm \phi}\left( \sqrt{2 \pi }\cdot{t}/{\Delta t} \right) \hspace{0.7cm}{\rm{mit}}\hspace{0.7cm}{\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$
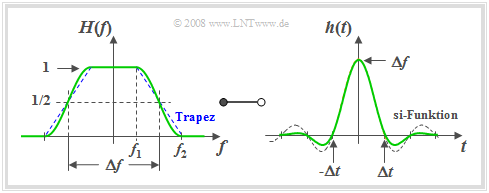
Trapez–Tiefpass
Die bisher in diesem Kapitel beschriebenen Tiefpassfunktionen hängen nur von einem Parameter – der äquivalenten Bandbreite $Δf$ – ab. Dabei war die Flankensteilheit für einen gegebenen Filtertyp fest vorgegeben.
Nun wird ein Tiefpass mit parametrisierbarer Flankensteilheit beschrieben.
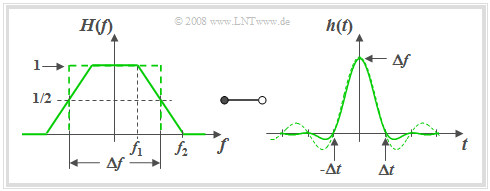
$\text{Definition:}$ Der Frequenzgang des Trapez–Tiefpasses lautet mit den Eckfrequenzen $f_1$ und $f_2 \ge f_1$:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 - \vert f \vert }{f_2 -f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{für} \\ \text{für} \\ \text{für} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ {f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert > f_2.} \\ \end{array}$$
Anstelle von $f_1$ und $f_2$ kann man zur Beschreibung von $H(f)$ auch folgende Parameter verwenden:
- die äquivalente Bandbreite, ermittelt über das flächengleiche Rechteck:
- $$\Delta f = f_1 + f_2.$$
- der Rolloff-Faktor (im Frequenzbereich) als Maß für die Flankensteilheit:
- $$r_{\hspace{-0.05cm}f} = \frac{f_2 - f_1}{f_2 + f_1}.$$
Als Sonderfälle sind in der allgemeinen Darstellung enthalten:
- der ideale rechteckförmige Tiefpass $(r_{\hspace{-0.05cm}f} = 0)$,
- der Dreiecktiefpass $(r_{\hspace{-0.05cm}f} = 1)$.
Die folgende Grafik zeigt für den Rolloff–Faktor $r_f = 0.5 \ \Rightarrow \ f_2 = 3f_1$ links den Frequenzgang $H(f)$ und rechts die Impulsantwort
- $$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t )\cdot {\rm si}(\pi \cdot r_{\hspace{-0.05cm}f} \cdot \Delta f \cdot t )\hspace{0.7cm}{\rm{mit}}\hspace{0.7cm}{\rm si}(x) = {\sin(x)}/{x}.$$
Der $\rm si$–Zeitverlauf des rechteckförmigen Tiefpasses mit gleicher äquivalenter Bandbreite ist zum Vergleich gestrichelt eingezeichnet.
Die Grafik sowie obige Gleichungen erlauben folgende Aussagen:
- Die Trapezform entsteht zum Beispiel durch die Faltung zweier Rechtecke der Breiten $Δf$ und $r_f \cdot Δf$.
- Entsprechend dem Faltungssatz ist somit die Impulsantwort das Produkt zweier $\rm si$–Funktionen mit den Argumenten $π · Δf · t$ und $π · r_{\hspace{-0.05cm}f} · Δf · t$.
- Die erste $\rm si$–Funktion ist für alle Werte von $r_{\hspace{-0.05cm}f}$ Bestandteil der Gleichung für $h(t)$ und führt stets zu äquivalenten Nulldurchgängen im Abstand $1/Δf$.
- Für $0 \lt r_{\hspace{-0.05cm}f} \lt 1$ gibt es weitere Nullstellen bei Vielfachen von $Δt/r_{\hspace{-0.05cm}f}$.
- Der asymptotische Abfall der Impulsantwort $h(t)$ erfolgt um so schneller, je größer $r_{\hspace{-0.05cm}f}$ ist, das heißt bei gegebenem $Δf$ mit flacherer Flanke.
- Der schnellstmögliche Abfall ergibt sich beim Dreiecktiefpass ⇒ $r_{\hspace{-0.05cm}f} = 1$, $f_1 = 0$, $f_2 = Δf$. Für diesen gilt im Frequenz– und Zeitbereich:
- $$H(f) = \left\{ \begin{array}{c} \hspace{0.25cm} \frac{{\rm \Delta}f -|f|}{{\rm \Delta}f} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\hspace{1cm} \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le {\rm \Delta}f ,} \\ {\hspace{1cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| \ge {\rm \Delta}f } \\ \end{array}, \hspace{1cm} h(t) = \Delta f \cdot {\rm si}^2(\pi \cdot \Delta f \cdot t )\hspace{0.4cm}{\rm{mit}}\hspace{0.4cm}{\rm si}(x) = \frac{\sin(x)}{x}.$$
Cosinus-Rolloff-Tiefpass
Ebenso wie der Trapez–Tiefpass wird dieser Tiefpass durch zwei Parameter beschrieben, nämlich durch
- die äquivalente Bandbreite $Δf$ und
- den Rolloff–Faktor $r_{\hspace{-0.05cm}f}$.
Dessen Wertebereich liegt zwischen $r_{\hspace{-0.05cm}f} = 0$ (Rechtecktiefpass) und $r_{\hspace{-0.05cm}f} = 1$ (Cosinus–Quadrat–Tiefpass).
$\text{Definition:}$ Mit den Eckfrequenzen $f_1 = Δf · (1 – r_{\hspace{-0.05cm}f})$ und $f_2 = Δf · (1 + r_{\hspace{-0.05cm}f})$ lautet der Frequenzgang des Cosinus–Rolloff–Tiefpasses:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \cos \left( \frac{ \vert f \vert - f_1}{f_2 -f_1}\frac{\pi}{2}\right) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{für} \\ \text{für} \\ \text{für} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ {f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert> f_2.} \\ \end{array}$$
Die Grafik zeigt links $H(f)$ sowie rechts die Impulsantwort
- $$h(t) = \Delta f \hspace{-0.05cm}\cdot\hspace{-0.05cm} {\rm si}(\pi \hspace{-0.05cm}\cdot\hspace{-0.05cm} \Delta f \hspace{-0.05cm}\cdot\hspace{-0.05cm} t )\hspace{-0.05cm}\cdot\hspace{-0.05cm} \frac {\cos(\pi \cdot r_{\hspace{-0.05cm}f} \cdot \Delta f \cdot t )}{1 - (2 \cdot r_f \cdot \Delta f \cdot t)^2}.$$
Für diese Grafiken wurde der Rolloff–Faktor $r_{\hspace{-0.05cm}f} = 0.5$ verwendet, das heißt, es gilt $f_2 = 3 \cdot f_1$.
Gestrichelt sind zum Vergleich eingezeichnet:
- im Frequenzbereich der Trapeztiefpass und
- im Zeitbereich die $\rm si$–Funktion.
Es ist zu beachten:
- Die $\rm si$–Funktion ist nicht die Fourierrücktransformierte des links blau eingezeichneten Trapeztiefpasses.
- Sie beschreibt vielmehr den (nicht dargestellten) idealen, rechteckförmigen Tiefpass im Zeitbereich.
Anhand dieser Grafik und den obigen Gleichungen sind folgende Aussagen möglich:
- Die Impulsantwort $h(t)$ des Cosinus–Rolloff–Tiefpasses hat bei allen Vielfachen von $Δt = 1/Δf$ Nullstellen, die auf die im rechten Bild gestrichelt eingezeichnete si–Funktion zurückzuführen sind.
- Der letzte Term in der $h(t)$–Gleichung führt zu weiteren Nullstellen bei Vielfachen von $Δt/r_f$. Ist $1/r_f$ ganzzahlig wie in obiger Grafik $(1/r_f = 2)$, so fallen diese neuen Nullstellen mit den anderen Nullstellen zusammen, sind also nicht erkennbar.
- Je größer der Rolloff-Faktor $r_f$ ist und je flacher damit der Flankenabfall erfolgt, desto günstiger ist im Allgemeinen das Einschwingverhalten des Cosinus-Rolloff-Tiefpasses.
- Der Cosinus–Rolloff–Tiefpass zeigt meist ein besseres asymptotisches Einschwingverhalten als der Trapez–Tiefpass mit gleichem $r_f$, obwohl dieser zumindest bei $Δf/2$ eine flachere Flanke aufweist.
- Dies lässt darauf schließen, dass das Einschwingverhalten nicht nur durch Unstetigkeitsstellen (wie beim Rechteck), sondern auch durch Knickpunkte wie beim Trapez–Tiefpass beeinträchtigt wird.
$\text{Definition:}$ Als Sonderfall ergibt sich mit $f_1 = 0$, $f_2 = Δf$ ⇒ $r_f = 1$ der Cosinus–Quadrat–Tiefpass, dessen Impulsantwort auch wie folgt dargestellt werden kann:
- $$h(t) = \frac{1}{ \Delta t}\cdot{\rm si}(\pi \frac{t}{ \Delta t}) \cdot \left[ {\rm si}(\pi \frac{t}{ \Delta t} + 0.5) - {\rm si}(\pi \frac{t}{ \Delta t} - 0.5) \right].$$
- Diese Funktion hat Nullstellen bei $t/Δt = ±1, ±1.5, ±2, ±2.5$ usw., nicht jedoch bei $t/Δt = ±0.5$.
- Der Cosinus–Quadrat–Tiefpass erfüllt als einziger Tiefpass beide Nyquistkriterien ⇒ siehe Buch Digitalsignalübertragung.
Herleitung systemtheoretischer Hochpassfunktionen
Bisher wurden in diesem Kapitel fünf häufig verwendete systemtheoretische Tiefpassfunktionen betrachtet. Für jede einzelne Tiefpassfunktion lässt sich auch eine äquivalente Hochpassfunktion angeben.
$\text{Definition:}$ Ist $H_{\rm TP}(f)$ eine systemtheoretische TP–Funktion mit $H_{\rm TP}(f = 0) = 1$, so ist die äquivalente Hochpassfunktion:
- $$H_{\rm HP}(f) = 1 - H_{\rm TP}(f).$$
Damit lauten die Beschreibungsgrößen im Zeitbereich:
- $$h_{\rm HP}(t) = \delta (t) - h_{\rm TP}(t),\hspace{1cm} \sigma_{\rm HP}(t) = \gamma (t) - \sigma_{\rm TP}(t). $$
Hierbei bezeichnen:
- $h_{\rm HP}(t)$ und $h_{\rm TP}(t)$ die Impulsantworten von Hoch– und Tiefpass,
- $σ_{\rm HP}(t)$ und $σ_{\rm TP}(t)$ die dazugehörigen Sprungantworten,
- $γ(t)$ die Sprungfunktion als Ergebnis der Integration über die Diracfunktion $δ(t)$.
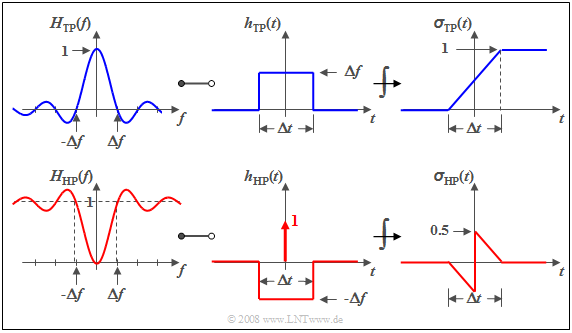
$\text{Beispiel 1:}$ Wir betrachten den Spalttiefpass, der sich durch einen $\rm si$–förmigen Frequenzgang, eine rechteckförmige Impulsantwort und eine linear ansteigende Sprungantwort auszeichnet. Diese sind in der nachfolgenden Grafik dargestellt.
Die untere Skizze zeigt die entsprechenden Hochpassfunktionen.
Man erkennt, dass
- $H_{\rm HP}(f = 0)$ immer den Wert $0$ besitzt, wenn $H_{\rm TP}(f = 0) = 1$ ist,
- demzufolge das Integral über $h_{\rm HP}(t)$ ebenfalls Null ergeben muss, und
- auch die Sprungantwort $σ_{\rm HP}(t)$ gegen den Endwert Null tendiert.
Aufgaben zum Kapitel
Aufgabe 1.5: Idealer rechteckförmiger Tiefpass
Aufgabe 1.5Z: si-förmige Impulsantwort
Aufgabe 1.6: Rechtförmeckige Impulsantwort
Aufgabe 1.6Z: Interpretation der Übertragungsfunktion
Aufgabe 1.7: Nahezu kausaler Gaußtiefpass
Aufgabe 1.8: Variable Flankensteilheit
Aufgabe 1.8Z: Cosinus-Quadrat-Tiefpass