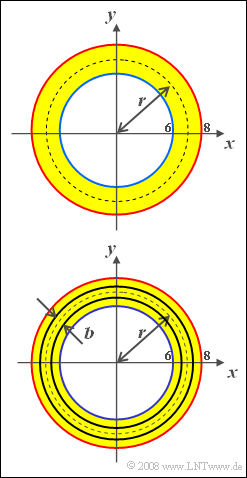
Aufgabe 3.8Z: Kreis(ring)fläche

Kreisringflächen

Wir betrachten unterschiedlich große Kreise:

Radius $r$ und Fläche $A$ lassen sich als voneinander abhängige Zufallsgrößen auffassen.
Es wird vorausgesetzt, dass der Radius auf den Bereich $6 \le r \le 8$ beschränkt ist.

In der oberen Skizze ist der Bereich, in dem solche Kreise (alle mit Mittelpunkt im Koordinatenursprung) liegen können, gelb markiert. Weiterhin kann davon ausgegangen werden, dass der Radius in diesem Intervall gleichverteilt ist:

$$f_r(r)=\left\{ \begin{array}{*{4}{c}} 0.5 & \rm f\ddot{u}r\hspace{0.2cm}{\rm 6\le \it r \le \rm 8}, \\\rm 0 & \rm sonst. \end{array} \right.$$

Ab der Teilaufgabe (5) werden schmale Kreisringe mit dem Mittelradius $r$ und der Breite $b$ betrachtet (untere Skizze):

Die Fläche eines solchen Kreisrings wird mit $R$ bezeichnet.
Die möglichen Mittelradien $r$ seien wieder gleichverteilt zwischen $6$ und $8$.
Die Kreisringbreite beträgt $b = 0.1$.

Hinweise:

Die Aufgabe gehört zum Kapitel Exponentialverteilte Zufallsgrößen.
Insbesondere wird Bezug genommen auf die Seite Transformation von Zufallsgrößen.

Fragebogen

$A_\text{min} \ = \ $

$A_\text{max} \ = \ $

$m_{ A} \ = \ $

${\rm Pr}(A > 150) \ = \ $

$R_\text{min} \ = \ $

$R_\text{max} \ = \ $

${\rm E}\big[R\big] \ = \ $

Musterlösung

(1) Die Gleichung der Kreisfläche ist gleichzeitig die Transformationskennlinie: $A = \pi \cdot r^2$.
Daraus ergibt sich mit $r = 6$ für den Minimalwert: $A_\text{min} \hspace{0.15cm}\underline {= 113.09}$.

(2) Entsprechend gilt mit $r = 8$ für den Maximalwert: $A_\text{max} \hspace{0.15cm}\underline {= 201.06}$.

(3) Am einfachsten löst man diese Aufgabe wie folgt:

$$m_{\rm A}={\rm E}\big[A\big]={\rm E}\big[g(r)\big]=\int_{ -\infty}^{+\infty}g(r)\cdot f_r(r) {\rm d}r.$$

Mit $g(r) = \pi \cdot r^2$ und $f_r(r) = 1/2$ im Bereich von $6$ ... $8$ erhält man:

$$m_{\rm A}=\int_{\rm 6}^{\rm 8}1/2 \cdot\pi\cdot r^{\rm 2}\, {\rm d} \it r=\frac{\pi}{\rm 6}\cdot \rm ( 8^3-6^3) \hspace{0.15cm}\underline{=\rm 154.98}.$$

(4) Die WDF der transformierten Zufallsgröße $A$ lautet:

$$f_A(A)=\frac{f_r(r)}{|g\hspace{0.05cm}'(r)|}\Bigg|_{r=h(y) = \sqrt{A/ \pi }}.$$

Im Bereich zwischen $A_\text{min} {= 113.09}$ und $A_\text{max} {= 201.06}$ gilt dann:

$$f_A(A)=\frac{\rm 1/2}{\rm 2\cdot \pi\cdot\it r}\Bigg|_{\it r=\sqrt{\it A/\rm \pi}}=\frac{\rm 1}{\rm 4\cdot\sqrt{\it A\cdot\rm \pi}}.$$

Die gesuchte Wahrscheinlichkeit erhält man durch Integration:

$${\rm Pr}(A> 150)=\int_{\rm 150}^{\it A_{\rm max}}\frac{\rm 1}{\rm 4\cdot\sqrt{\it A\cdot\rm \pi}} \; \rm d \it A= \frac{\rm 2\cdot\sqrt{\it A}}{\rm 4\cdot\sqrt{\pi}}\Big|_{\rm 150}^{\it A_{\rm max}}.$$

Die obere Integrationsgrenze liefert den Wert $4$ und die untere Grenze $3.455$. Daraus ergibt sich die gesuchte Wahrscheinlichkeit:

$${\rm Pr}(A> 150) \hspace{0.15cm}\underline {=0.545}.$$

(5) Für die Kreisringfläche $R$ gilt bei gegebenem Radius $r$:

$$R=\left (r+{b}/{\rm 2} \right)^{\rm 2}\cdot \rm\pi-\left ({\it r}-{\it b}/{\rm 2} \right)^{\rm 2}\cdot \rm\pi= \rm2\cdot\pi\cdot\it r \cdot b.$$

Zwischen $R$ und $r$ besteht also ein linearer Zusammenhang.
Das heißt, $R$ ist ebenfalls gleichverteilt und zwar unabhängig von der Breite $b$, solange $b \ll r$ ist.
Für den Minimalwert gilt:

$$R_{\rm min}=\rm 2\pi\cdot 6\cdot 0.1\hspace{0.15cm}\underline{\approx3.77}. $$

(6) Entsprechend ist der Maximalwert:

$$R_{\rm max}=\rm 2\pi\cdot 8\cdot 0.1\hspace{0.15cm}\underline{\approx 5.03}.$$

(7) Aufgrund des linearen Zusammenhangs zwischen $R$ und $r$ führt der mittlere Radius $r = 7$ auch zur mittleren Kreisringfläche:

$${\rm E}\big[R\big]=\rm 2\pi\cdot 7\cdot 0.1\hspace{0.15cm}\underline{\approx 4.4}.$$