Impulse und Spektren

Inhaltsverzeichnis

1 Programmbeschreibung
2 Theoretischer Hintergrund
3 Versuchsdurchführung
4 Zur Handhabung des Programms
5 Über die Autoren
6 Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Programmbeschreibung

Dargestellt werden impulsförmige symmetrische Zeitsignale ⇒ „Impulse” $x(t)$ und die dazugehörigen Spektralfunktionen $X(f)$, nämlich

Gaußimpuls (englisch: Gaussian pulse),
Rechteckimpuls (englisch: Rectangular pulse),
Dreieckimpuls (englisch: Triangular pulse),
Trapezimpuls (englisch: Trapezoidal pulse),
Cosinus–Rolloff–Impuls (englisch: Cosine-rolloff pulse).

Weiter ist zu beachten:

Die Funktionen $x(t)$ bzw. $X(f)$ werden für bis zu zwei Parametersätzen in jeweils einem Diagramm dargestellt.
Die roten Kurven und Zahlenangaben gelten für den linken Parametersatz, die blauen für den rechten Parametersatz.
Die Abszissen $t$ (Zeit) und $f$ (Frequenz) sowie die Ordinaten $x(t)$ (Signalwerte) bzw. $X(f)$ (Spektralwerte) sind jeweils normiert.

Theoretischer Hintergrund

Zusammenhang $x(t)\Leftrightarrow X(f)$

Der Zusammenhang zwischen der Zeitfunktion $x(t)$ und dem Spektrum $X(f)$ ist durch das erste Fourierintegral gegeben:

$$X(f)={\rm FT} [x(t)] = \int_{-\infty}^{+\infty}x(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} \rm FT\hspace{-0.1cm}: \ Fouriertransformation.$$

Um aus der Spektralfunktion $X(f)$ die Zeitfunktion $x(t)$ berechnen zu können, benötigt man das zweite Fourierintegral:

$$x(t)={\rm IFT} [X(f)] = \int_{-\infty}^{+\infty}X(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fouriertransformation.$$

In allen Beispielen verwenden wir reelle und gerade Funktionen. Somit gilt:

$$x(t)=\int_{-\infty}^{+\infty}X(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ X(f)=\int_{-\infty}^{+\infty}x(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$

$x(t)$ und $X(f)$ haben unterschiedliche Einheiten, beispielsweise $x(t)$ in $\rm V$, $X(f)$ in $\rm V/Hz$.
Der Zusammenhang zwischen diesem Modul und dem ähnlich aufgebauten Applet Frequenzgang & Impulsantwort basiert auf dem Vertauschungssatz.
Alle Zeiten sind auf eine Zeit $T$ normiert und alle Frequenzen auf $1/T$ ⇒ die Spektralwerte $X(f)$ müssen noch mit der Normierungszeit $T$ multipliziert werden.

$\text{Beispiel:}$ Stellt man einen Rechteckimpuls mit Amplitude $A_1 = 1$ und äquivalenter Impulsdauer $\Delta t_1 = 1$ ein, so ist $x_1(t)$ im Bereich $-0.5 < t < +0.5$ gleich Eins und außerhalb dieses Bereichs gleich Null. Die Spektralfunktion $X_1(f)$ verläuft $\rm si$–förmig mit $X_1(f= 0) = 1$ und der ersten Nullstelle bei $f=1$.

Soll mit dieser Einstellung ein Rechteckimpuls mit $A = K = 3 \ \rm V$ und $\Delta t = T = 2 \ \rm ms$ nachgebildet werden, dann sind alle Signalwerte mit $K = 3 \ \rm V$ und alle Spektralwerte mit $K \cdot T = 0.006 \ \rm V/Hz$ zu multiplizieren.
Der maximale Spektralwert ist dann $X(f= 0) = 0.006 \ \rm V/Hz$ und die erste Nullstelle liegt bei $f=1/T = 0.5 \ \rm kHz$.

Gaußimpuls $\Rightarrow$ Gaussian Pulse

Die Zeitfunktion des Gaußimpulses mit der Höhe $K$ und der (äquivalenten) Dauer $\Delta t$ lautet:

$$x(t)=K\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/\Delta t)^2}.$$

Die äquivalente Zeitdauer $\Delta t$ ergibt sich aus dem flächengleichen Rechteck.
Der Wert bei $t = \Delta t/2$ ist um den Faktor $0.456$ kleiner als der Wert bei $t=0$.
Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta t \cdot {\rm e}^{-\pi(f\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t)^2} .$$

Je kleiner die äquivalente Zeitdauer $\Delta t$ ist, um so breiter und niedriger ist das Spektrum ⇒ Reziprozitätsgesetz von Bandbreite und Impulsdauer.
Sowohl $x(t)$ als auch $X(f)$ sind zu keinem $f$– bzw. $t$–Wert exakt gleich Null.
Für praktische Anwendungen kann der Gaußimpuls jedoch in Zeit und Frequenz als begrenzt angenommen werden. Zum Beispiel ist $x(t)$ bereits bei $t=1.5 \Delta t$ auf weniger als $0.1\% $ des Maximums abgefallen.

Rechteckimpuls $\Rightarrow$ Rectangular Pulse

Die Zeitfunktion des Rechteckimpulses mit der Höhe $K$ und der (äquivalenten) Dauer $\Delta t$ lautet:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < T/2,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| = T/2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| > T/2.} \\ \end{array}$$

Der $\pm \Delta t/2$–Wert liegt mittig zwischen links- und rechtsseitigem Grenzwert.
Für die Spektralfunktion erhält man entsprechend den Gesetzmäßigkeiten der Fouriertransformation (1. Fourierintegral):

$$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f) \quad \text{mit} \ {\rm si}(x)=\frac{\sin(x)}{x}.$$

Der Spektralwert bei $f=0$ ist gleich der Rechteckfläche der Zeitfunktion.
Die Spektralfunktion besitzt Nullstellen in äquidistanten Abständen $1/\Delta t$.
Das Integral über der Spektralfunktion $X(f)$ ist gleich dem Signalwert zum Zeitpunkt $t=0$, also der Impulshöhe $K$.

Dreieckimpuls $\Rightarrow$ Dreieckimpuls Triangular Pulse

Die Zeitfunktion des Dreieckimpulses mit der Höhe $K$ und der (äquivalenten) Dauer $\Delta t$ lautet:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot (1-|t|/{\Delta t}) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$

Die absolute Zeitdauer ist $2 \cdot \Delta t$; diese ist doppelt so groß als die des Rechtecks.
Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta t \cdot f) \quad \text{mit} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$

Obige Zeitfunktion ist gleich der Faltung zweier Rechteckimpulse, jeweils mit Breite $\Delta t$.
Daraus folgt: $X(f)$ beinhaltet anstelle der ${\rm si}$-Funktion die ${\rm si}^2$-Funktion.
$X(f)$ weist somit ebenfalls Nullstellen im äquidistanten Abständen $1/\Delta f$ auf.
Der asymptotische Abfall von $X(f)$ erfolgt hier mit $1/f^2$, während zum Vergleich der Rechteckimpuls mit $1/f$ abfällt.

Trapezimpuls $\Rightarrow$ Trapezoidal Pulse

Die Zeitfunktion des Trapezimpulses mit der Höhe $K$ und den Zeitparametern $t_1$ und $t_2$ lautet:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{t_2-|t|}{t_2-t_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}} \quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$

Für die äquivalente Impulsdauer (flächengleiches Rechteck) gilt: $\Delta t = t_1+t_2$.
Der Rolloff-Faktor (im Zeitbereich) kennzeichnet die Flankensteilheit:

$$r=\frac{t_2-t_1}{t_2+t_1}.$$

Der Sonderfall $r=0$ entspricht dem Rechteckimpuls und der Sonderfall $r=1$ dem Dreieckimpuls.
Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f)\cdot {\rm si}(\pi \cdot r \cdot \Delta t \cdot f) \quad \text{mit} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$

Der asymptotische Abfall von $X(f)$ liegt zwischen $1/f$ $($für Rechteck, $r=0)$ und $1/f^2$ $($für Dreieck, $r=1)$.

Cosinus-Rolloff-Impuls $\Rightarrow$ Cosine-rolloff Pulse

Die Zeitfunktion des Cosinus-Rolloff-Impulses mit der Höhe $K$ und den Zeitparametern $t_1$ und $t_2$ lautet:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|t|-t_1}{t_2-t_1}\cdot {\pi}/{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$

Für die äquivalente Impulsdauer (flächengleiches Rechteck) gilt: $\Delta t = t_1+t_2$.
Der Rolloff-Faktor (im Zeitbereich) kennzeichnet die Flankensteilheit:

$$r=\frac{t_2-t_1}{t_2+t_1}.$$

Der Sonderfall $r=0$ entspricht dem Rechteckimpuls und der Sonderfall $r=1$ dem Cosinus-Quadrat-Impuls.
Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta t \cdot \frac{\cos(\pi \cdot r\cdot \Delta t \cdot f)}{1-(2\cdot r\cdot \Delta t \cdot f)^2} \cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$

Je größer der Rolloff-Faktor $r$ ist, desto schneller nimmt $X(f)$ asymptotisch mit $f$ ab.

Cosinus-Quadrat-Impuls

Dies ist ein Sonderfall des Cosinus-Rolloff-Impulses und ergibt sich für $r=1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1=0, \ t_2= \Delta t$:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|t|\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$

Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta f \cdot \frac{\pi}{4}\cdot \big [{\rm si}(\pi(\Delta t\cdot f +0.5))+{\rm si}(\pi(\Delta t\cdot f -0.5))\big ]\cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$

Wegen der letzten ${\rm si}$-Funktion ist $X(f)=0$ für alle Vielfachen von $F=1/\Delta t$. Die äquidistanten Nulldurchgänge des Cos-Rolloff-Impulses bleiben erhalten.
Aufgrund des Klammerausdrucks weist $X(f)$ nun weitere Nulldurchgänge bei $f=\pm1.5 F$, $\pm2.5 F$, $\pm3.5 F$, ... auf.
Für die Frequenz $f=\pm F/2$ erhält man die Spektralwerte $K\cdot \Delta t/2$.
Der asymptotische Abfall von $X(f)$ verläuft in diesem Sonderfall mit $1/f^3$.

Versuchsdurchführung

Wählen Sie zunächst die Nummer $(1,\ 2$, ... $)$ der zu bearbeitenden Aufgabe. Die Nummer $0$ entspricht einem „Reset”: Einstellung wie beim Programmstart.
Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. Lösung nach Drücken von „Musterlösung”.
„Rot” bezieht sich auf den ersten Parametersatz ⇒ $x_1(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_1(f)$ und „Blau” auf den zweiten Parametersatz ⇒ $x_2(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_2(f)$.
Werte betragsmäßig kleiner $0.0005$ werden im Programm zu Null gesetzt.

(1) Vergleichen Sie den roten Gaußimpuls $(A_1 = 1, \Delta t_1 = 1)$ mit dem blauen Rechteckimpuls $(A_2 = 1, \Delta t_2 = 1)$ ⇒ Voreinstellung.
Welche Unterschiede erkennt man im Zeit- und im Frequenzbereich?

Der Gaußimpuls reicht sowohl im Zeit– als auch im Frequenzbereich theoretisch bis ins Unendliche.
Praktisch sind aber $x_1(t)$ für $|t| > 1.5$ und $X_1(f)$ für $|f| > 1.5$ nahezu Null.
Das Rechteck ist zeitlich steng begrenzt: $x_2(|t| > 0.5) \equiv 0$. $X_2(f)$ hat in einem viel größeren Bereich als $X_1(f)$ Anteile.
Es gilt $X_1(f = 0) = X_2(f = 0)$, weil das Integral über den Gaußimpuls $x_1(t)$ gleich dem Integral über den Rechteckimpuls $x_2(t)$ ist.

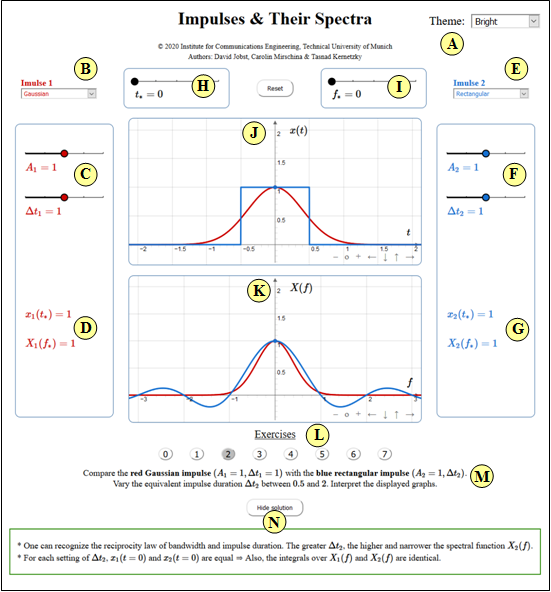
(2) Vergleichen Sie den roten Gaußimpuls $(A_1 = 1, \Delta t_1 = 1)$ mit dem blauen Rechteckimpuls $(A_2 = 1,\Delta t_2)$.
Variieren Sie die äquivalente Impulsdauer $\Delta t_2$ zwischen $0.5$ und $2$. Interpretieren Sie die dargestellten Graphen.

Man erkennt das Reziprozitätsgesetz von Bandbreite und Impulsdauer. Je größer $\Delta t_2$ ist, um so höher und schmäler ist die Spektralfunktion $X_2(f)$.
Bei jeder Einstellung von $\Delta t_2$ sind die Zeitsignalwerte $x_1(t= 0)$ und $x_2(t=0)$ gleich ⇒ Auch die Integrale über $X_1(f)$ und $X_2(f)$ sind identisch.

(3) Vergleichen Sie den roten Rechteckimpuls $(A_1 = 1, \Delta t_1 = 1)$ mit dem blauen Rechteckimpuls $(A_2 = 1,\Delta t_2 = 0.5)$.
Variieren Sie $\Delta t_2$ zwischen $0.05$ und $2$. Interpretieren Sie die dargestellten Graphen und extrapolieren Sie das Ergebnis.

Das blaue Spektrum ist nun doppelt so breit wie das rote, aber nur halb so hoch. Erste Nullstelle von $X_1(f)$ bei $f =1$ und von $X_2(f)$ erst bei $f =2$.
Verkleinerung von $\Delta t_2$: $X_2(f)$ immer niedriger und breiter. Sehr flacher Verlauf bei $\Delta t_2 = 0.05$: $X_2(f = 0)= 0.05$, $X_2(f = \pm 3)= 0.048$.
Würde man $\Delta t_2 = \varepsilon \to 0$ wählen (im Programm nicht möglich), so ergäbe sich das nahezu konstante, sehr kleine Spektrum $X_2(f)=A \cdot \varepsilon \to 0$.
Erhöht man die Amplitude auf $A=1/\varepsilon$, so ergibt sich die konstante Spektralfunktion $X_2(f) = 1$ der Diracfunktion $\delta(t)$. Das bedeutet:
$\delta(t)$ ist durch ein Rechteck mit Breite $\Delta t = \varepsilon \to 0$ und Höhe $A = 1/\varepsilon \to \infty$ approximierbar. Das Diracgewicht ist Eins: $x(t) = 1 \cdot \delta (t)$.

(4) Vergleichen Sie den Rechteckimpuls $(A_1 = 1, \Delta t_1 = 1)$ mit dem Dreieckimpuls $(A_2 = 1,\Delta t_2 = 1)$. Interpretieren Sie die Spektalfunktionen.

Das (normierte) Spektrum des Rechtecks $x_1(t)$ mit den (normierte) Parametern $A_1 = 1, \ \Delta t_1 = 1$ lautet: $X_1(f)= {\rm si}(\pi\cdot f)$.
Die Faltung des Rechtecks $x_1(t)$ mit sich selbst ergibt das Dreieck $x_2(t) = x_1(t) \star x_1(t)$. Nach dem Faltungssatz gilt somit $X_2(f) = \big [X_1(f)\big]^2 $.
Durch das Quadrieren der $\rm si$–förmigen Spektralfunktion $X_1(f)$ bleiben die Nullstellen in $X_2(f)$ erhalten. Es gilt aber nun $X_2(f) \ge 0$.

(5) Vergleichen Sie den Trapezimpuls $(A_1 = 1, \Delta t_1 = 1, r_1 = 0.5)$ mit dem Dreieckimpuls $(A_2 = 1,\Delta t_2 = 1)$.
Variieren Sie $r_1$ zwischen $0$ und $1$. Interpretieren Sie die Spektalfunktion $X_1(f)$.

Der Trapezimpuls mit Rolloff-Faktor $r_1= 0$ ist identisch mit dem Rechteckimpuls. Das „normierte Spektrum” lautet: $X_1(f)= {\rm si}(\pi\cdot f)$.
Der Trapezimpuls mit Rolloff-Faktor $r_1= 1$ ist identisch mit dem Dreieckimpuls. Das „normierte Spektrum” lautet: $X_1(f)= {\rm si}^2(\pi\cdot f)$.
In beiden Fällen besitzt $X_1(f)$ äquidistante Nulldurchgänge bei $\pm 1$, $\pm 2$, ... (sonst keine). Mit $0 < r_1 < 1$ gibt es abhängig von $r_1$ weitere Nulldurchgänge.

(6) Vergleichen Sie den Trapezimpuls $(A_1 = 1, \Delta t_1 = 1, r_1 = 0.5)$ mit dem Cosinus-Rolloff-Impuls $(A_2 = 1,\Delta t_2 = 1.0, r_1 = 0.5)$.
Variieren Sie $r_2$ zwischen $0$ und $1$. Interpretieren Sie die Spektalfunktion $X_2(f)$ für $r_2 = 0.7$.

Bei gleichem $r= 0.5$ besitzt der Cosinus-Rolloff-Impuls $X_2(f)$ ⇒ für $f > 1$ betragsmäßig größere Anteile als der Trapezimpuls.
Bei gleichem Rolloff-Faktor $(r_1 = r_2= 0.5)$ verläuft der Abfall von $X_2(f)$ um die Frequenz $f = 0.5$ steiler als der Abfall von $X_1(f)$.
Mit $r_1 = 0.5$ und $r_2 = 0.7$ gilt $x_1(t) \approx x_2(t)$ und damit auch $X_1(f) \approx X_2(f)$. Vergleichbare Flankensteilheit.

(7) Vergleichen Sie den roten Trapezimpuls $(A_1 = 1, \Delta t_1 = 1, r_1 = 1)$ mit dem blauen Cosinus-Rolloff-Impuls $(A_2 = 1,\Delta t_2 = 1.0, r_2 = 1)$.
Interpretieren Sie die Zeitfunktion $x_2(t)$ und die Spektralfunktion $X_2(f)$ systemtheoretisch.

Es handelt sich bei $x_2(t) = \cos^2(|t|\cdot \pi/2) \ \ \text{für} \ |t| \le 1$ um den Cosinus-Quadrat-Impuls. Nulldurchgänge bei $f = \pm 1$, $\pm 2$, ...
Für die Frequenz $f=\pm 0.5$ erhält man die Spektralwerte $X_2(f)=0.5$. Der asymptotische Abfall verläuft hier mit $1/f^3$.

Zur Handhabung des Programms

Bildschirmabzug (englische Version, heller Hintergrund)

(A) Theme (veränderbare grafische Oberflächengestaltung)

Dark: schwarzer Hintergrund (wird von den Autoren empfohlen)
Bright: weißer Hintergrund (empfohlen für Beamer und Ausdrucke)
Deuteranopia: für Nutzer mit ausgeprägter Grün–Sehschwäche
Protanopia: für Nutzer mit ausgeprägter Rot–Sehschwäche

(B) Vorauswahl für die Impulsform $x_1(t)$ (rote Kurve)

(C) Parameterfestlegung für $x_1(t)$

(D) Numerikausgabe für $x_1(t_*)$ und $X_1(f_*)$

(E) Vorauswahl für die Impulsform $x_2(t)$ (blaue Kurve)

(F) Parameterfestlegung für $x_2(t)$

(G) Numerikausgabe für $x_2(t_*)$ und $X_2(f_*)$

(H) Einstellung der Zeit $t_*$ für die Numerikausgabe

(I) Einstellung der Frequenz $f_*$ für die Numerikausgabe

(J) Bereich der graphischen Darstellung im Zeitbereich

(K) Bereich der graphischen Darstellung im Frequenzbereich

(L) Auswahl der Aufgabe entsprechend der Aufgabennummer

(M) Aufgabenbeschreibung und Fragestellung

(N) Musterlösung anzeigen und verbergen

Details zu den obigen Punkten (J ) und (K)

Zoom–Funktionen:
„$+$” (Vergrößern), „$-$” (Verkleinern), „$\rm o$” (Zurücksetzen)

Verschiebe–Funktionen: „$\leftarrow$” „$\uparrow$” „$\downarrow$” „$\rightarrow$”
„$\leftarrow$” bedeutet: Bildausschnitt nach links, Ordinate nach rechts

Andere Möglichkeiten:

Bei gedrückter Shifttaste und Scrollen kann im Koordinatensystem gezoomt werden.
Bei gedrückter Shifttaste und gedrückter linker Maustaste kann das Koordinatensystem verschoben werden.

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

Die erste Version wurde 2005 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder und Klaus Eichin).
2017 wurde „Impulse & Spektren” von David Jobst im Rahmen seiner Ingenieurspraxis (Betreuer: Tasnád Kernetzky) auf „HTML5” umgesetzt und neu gestaltet.
Letztmalige Überarbeitung 2020 durch Carolin Mirschina im Rahmen einer Werkstudententätigkeit.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Applet in neuem Tab öffnen