Aufgabe 1.4: Entropienäherungen für den AMI-Code
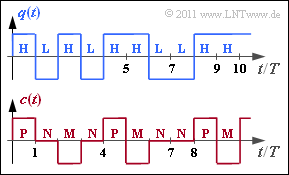
Die Grafik zeigt oben das binäre Quellensignal $q(t)$, das man ebenfalls durch die Symbolfolge $\langle q_\nu \rangle$ mit $q_\nu \in \{ {\rm L}, {\rm H} \}$ beschreiben kann. In der gesamten Aufgabe gelte $p_{\rm L} = p_{\rm H} =0.5$.
Das codierte Signal $c(t)$ und die dazugehörige Symbolfolge $\langle c_\nu \rangle$ mit $c_\nu \in \{{\rm P}, {\rm N}, {\rm M} \}$ ergibt sich aus der AMI–Codierung (Alternate Mark Inversion) nach folgender Vorschrift:
- Das Binärsymbol $\rm L$ ⇒ Low wird stets durch das Ternärsymbol $\rm N$ ⇒ Null dargestellt.
- Das Binärsymbol $\rm H$ ⇒ High wird ebenfalls deterministisch, aber alternierend (daher der Name „AMI”) durch die Symbole $\rm P$ ⇒ Plus und $\rm M$ ⇒ Minus codiert.
In dieser Aufgabe sollen die Entropienäherungen für das AMI–codierte Signal berechnet werden:
- Die Näherung $H_1$ bezieht sich nur auf die Symbolwahrscheinlichkeiten $p_{\rm P}$, $p_{\rm N}$ und $p_{\rm M}$.
- Die $k$–te Entropienäherung $(k = 2, 3, \text{...} \ )$ kann nach folgender Gleichung ermittelt werden:
- $$H_k = \frac{1}{k} \cdot \sum_{i=1}^{3^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_i^{(k)}} \hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol}) \hspace{0.05cm}.$$
- Hierbei bezeichnet $p_i^{(k)}$ die $i$–te Verbundwahrscheinlichkeit eines $k$–Tupels.
Hinweise:
- Die Aufgabe gehört zum Kapitel Nachrichtenquellen mit Gedächtnis.
- Bezug genommen wird insbesondere auf die Seite Die Entropie des AMI-Codes.
- In der Aufgabe 1.4Z wird die tatsächliche Entropie der Codesymbolfolge $\langle c_\nu \rangle$ zu $H = 1 \; \rm bit/Symbol$ berechnet.
- Zu erwarten sind die folgenden Größenrelationen: $H \le$ ...$ \le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$
Fragebogen
Musterlösung
- $$H_0 = {\rm log}_2\hspace{0.1cm} M = {\rm log}_2\hspace{0.1cm} (3) \hspace{0.15cm} \underline { = 1.585 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
(2) Die Entropienäherung erster Ordnung berücksichtigt nur die Symbolwahrscheinlichkeiten $p_{\rm P}$, $p_{\rm N}$ und $p_{\rm M}$ und nicht die statistischen Bindungen innerhalb der Codefolge $\langle c_\nu \rangle$. Damit erhält man:
- $$p_{\rm N} = p_{\rm L} = 1/2\hspace{0.05cm},\hspace{0.2cm}p_{\rm P} = p_{\rm M} = p_{\rm H}/2 = 1/4 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_1 = \frac{1}{2} \cdot {\rm log}_2\hspace{0.1cm} (2) + 2 \cdot \frac{1}{4} \cdot {\rm log}_2\hspace{0.1cm}(4) \hspace{0.15cm} \underline {= 1.5 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
(3) Zunächst müssen hier die $M^2 = 9$ Verbundwahrscheinlichkeiten von Zweiertupeln ermittelt werden, im Folgenden gekennzeichnet durch die beiden ersten Codesymbole $c_1$ und $c_2$:
- Da beim AMI–Code weder $\rm P$ auf $\rm P$ noch $\rm M$ auf $\rm M$ folgen kann, ist $p_{\rm PP} = p_{\rm MM} =0$.
- Für die Verbundwahrscheinlichkeiten unter der Bedingung $c_2 = \rm N$ gilt:
- $$p_{\rm NN} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{N}) \cdot {\rm Pr}(c_2 = \mathbf{N}\hspace{0.05cm} | c_1 = \mathbf{N}) = 1/2 \cdot 1/2 = 1/4 \hspace{0.05cm},$$
- $$ p_{\rm MN} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{M}) \cdot {\rm Pr}(c_2 = \mathbf{N}\hspace{0.05cm} | c_1 = \mathbf{M}) = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm},$$
- $$ p_{\rm PN} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{P}) \cdot {\rm Pr}(c_2 = \mathbf{N}\hspace{0.05cm} | c_1 = \mathbf{P}) = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm}.$$
- Die Verbundwahrscheinlichkeiten der Zweiertupel $\rm PM$ und $\rm MP$ lauten:
- $$p_{\rm PM} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{P}) \cdot {\rm Pr}(c_2 = \mathbf{M}\hspace{0.05cm} | c_1 = \mathbf{P}) = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm},$$
- $$ p_{\rm MP} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{M}) \cdot {\rm Pr}(c_2 = \mathbf{P}\hspace{0.05cm} | c_1 = \mathbf{M}) = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm}.$$
- Bei den restlichen Wahrscheinlichkeiten muss zusätzlich berücksichtigt werden, ob beim letzten Mal das Binärsymbol $\rm H$ mit $\rm P$ oder mit $\rm M$ codiert wurde ⇒ weiterer Faktor $1/2$:
- $$p_{\rm NM} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{N}) \cdot {\rm Pr}(c_2 = \mathbf{M}\hspace{0.05cm} | c_1 = \mathbf{N}) = 1/2 \cdot 1/2 \cdot 1/2= 1/8 \hspace{0.05cm},$$
- $$ p_{\rm NP} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}( c_1 = \mathbf{N}) \cdot {\rm Pr}(c_2 = \mathbf{P}\hspace{0.05cm} | c_1 = \mathbf{N}) = 1/2 \cdot 1/2 \cdot 1/2 = 1/8 \hspace{0.05cm}.$$
Damit ist die Entropie $H_2'$ eines Zweiertupels bzw. dessen Entropie $H_2$ pro Codesymbol:
- $$H_2\hspace{0.01cm}' = \frac{1}{4} \cdot {\rm log}_2\hspace{0.1cm} (4) + 6 \cdot \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8) \hspace{0.15cm} {= 2.75 \,{\rm bit/Zweiertupel}}\hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_2 = \frac{H_2\hspace{0.01cm}'}{2} \hspace{0.15cm} \underline {= 1.375 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
(4) Die Berechnung von $H_3$ erfolgt ähnlich wie bei der letzten Teilaufgabe für $H_2$, nur müssen nun $3^3 = 27$ Verbundwahrscheinlichkeiten ermittelt werden:
- $$p_{\rm NNN} = 1/8\hspace{0.4cm}{\rm (nur \hspace{0.15cm}einmal)} \hspace{0.05cm},$$
- $$p_{\rm NMM} = p_{\rm NPP} = p_{\rm MNM} = ... = 0 \hspace{0.4cm}{\rm (ingesamt \hspace{0.15cm}12)} \hspace{0.05cm},$$
- $$p_{\rm NNM} = p_{\rm NNP} = p_{\rm PMP} = ... = 1/16 \hspace{0.4cm}{\rm (ingesamt \hspace{0.15cm}14)}$$
- $$\Rightarrow\hspace{0.3cm} H_3 = \frac{1}{3} \cdot \left [ \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm} (8) + 14 \cdot \frac{1}{16} \cdot {\rm log}_2\hspace{0.1cm}(16) \right ] \hspace{0.15cm} \underline {= 1.292 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
(5) Richtig sind die Lösungsvorschläge 1 und 2.
- Falsch ist dagegen die Aussage 3, da $H_4$ auf jeden Fall kleiner sein muss als $H_3 = 1.292 \; \rm bit/Symbol$.