Stochastische Systemtheorie
Problemstellung
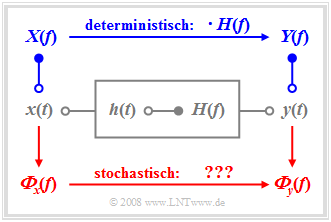
Wir betrachten wie im Buch Lineare zeitinvariante Systeme die unten skizzierte Anordnung, wobei das System sowohl durch die Impulsantwort $h(t)$ als auch durch seinen Frequenzgang $H(f)$ eindeutig beschrieben ist. Der Zusammenhang zwischen diesen beiden Beschreibungsgrößen im Zeit- und Frequenzbereich ist durch die Fouriertransformation gegeben.
Legt man an den Eingang das Signal $x(t)$ an und bezeichnet das Ausgangssignal mit $y(t)$, so liefert die klassische Systemtheorie folgende Aussagen:
- Das Ausgangssignal $y(t)$ ergibt sich aus der Faltung zwischen dem Eingangssignal $x(t)$ und der Impulsantwort $h(t)$:
$$y(t) = x(t) \ast h(t) = \int_{-\infty}^{+\infty} x(\tau)\cdot h ( t - \tau) \,\,{\rm d}\tau.$$
- Diese Gleichung gilt für deterministische und stochastische Signale gleichermaßen.
- Bei deterministischen Signalen geht man meist den Umweg über die Spektralfunktionen. Das Eingangsspektrum $X(f)$ ist die Fouriertransformierte von $x(t)$. Die Multiplikation mit dem Frequenzgang $H(f)$ führt zum Spektrum $Y(f)$. Das Signal $y(t)$ lässt sich daraus durch die Fourierrücktransformation gewinnen.
- Bei stochastischen Signalen versagt diese Vorgehensweise, da dann die Zeitfunktionen $x(t)$ und $y(t)$ nicht für alle Zeiten von $–∞$ bis $+∞$ vorhersagbar sind und somit die dazugehörigen Amplitudenspektren $X(f)$ und $Y(f)$ gar nicht existieren. In diesem Fall muss auf die in Kapitel 4.5 definierten Leistungsdichtespektren übergegangen werden.
Amplituden- und Leistungsdichtespektrum (1)
Wir betrachten nun einen ergodischen Zufallsprozess { $x(t)$}, dessen Autokorrelationsfunktion $φ_x(τ)$ als bekannt vorausgesetzt wird. Das Leistungsdichtespektrum $\it Φ_x(f)$ ist dann über die Fouriertransformation ebenfalls eindeutig bestimmt und es sind folgende Aussagen zutreffend:
- Das Leistungsdichtespektrum $\it Φ_x(f)$ kann – ebenso wie die Autokorrelationsfunktion $φ_x(τ)$ – für jede einzelne Musterfunktion des stationären und ergodischen Zufallsprozesses { $x(t)$} angegeben werden, auch wenn der spezifische Verlauf von $x(t)$ explizit nicht bekannt ist.
- Das Amplitudenspektrum $X(f)$ ist dagegen undefiniert, da bei Kenntnis der Spektralfunktion $X(f)$ auch die gesamte Zeitfunktion $x(t)$ von $–∞$ bis $+∞$ über die Fourierrücktransformation bekannt sein müsste, was eindeutig nicht der Fall sein kann.
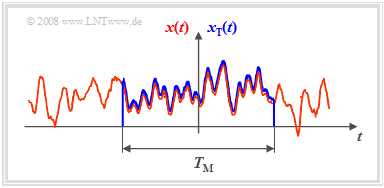
- Ist entsprechend der nachfolgenden Skizze ein Zeitausschnitt der endlichen Zeitdauer $T_{\rm M}$ bekannt, so kann für diesen natürlich wieder die Fouriertransformation angewandt werden.
- Zwischen dem Leistungsdichtespektrum $\it Φ_x(f)$ des unendlich ausgedehnten Zufallssignals $x(t)$ und dem Amplitudenspektrum $X_{\rm T}(f)$ des begrenzten Zeitausschnittes $x_{\rm T}(t)$ besteht dabei der folgende Zusammenhang:
$${\it \Phi_x(f)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot |X_{\rm T}(f)|^2.$$
Die Herleitung dieser wichtigen Beziehung folgt im nächsten Abschnitt. Sollten Sie sich für diesen mathematischen Beweis nicht interessieren, so können Sie gerne zum nachfolgenden Abschnitt Leistungsdichtespektrum des Filterausgangssignals springen.
Amplituden- und Leistungsdichtespektrum (2)
Es folgt der Beweis der auf der letzten Seite angegebenen Beziehung $${{\it \Phi}_x(f)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot |X_{\rm T}(f)|^2.$$
Beweis: In Kapitel 4.4 wurde die Autokorrelationsfunktion (AKF) eines ergodischen Prozesses mit der Musterfunktion $x(t)$ angegeben: $${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot x(t + \tau)\hspace{0.1cm} \rm d \it t.$$ Es ist hier zulässig, die zeitlich unbegrenzte Funktion $x(t)$ durch die auf den Zeitbereich $–T_{\rm M}/2$ bis $+T_{\rm M}/2$ begrenzte Funktion $x_{\rm T}(t)$ zu ersetzen. $x_{rm T}(t)$ korrespondiert mit der Spektralfunktion $X_{\rm T}(f)$, und man erhält durch Anwendung des Fourierintegrals und des Verschiebungssatzes: $${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot \int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x_{\rm T}(t)\cdot \int^{+\infty}_{-\infty}X_{\rm T}(f)\cdot {\rm e}^{{\rm j}2 \pi f ( t + \tau) } \hspace{0.1cm} \rm d \it f \hspace{0.1cm} \rm d \it t.$$ Nach Aufspalten des Exponenten und Vertauschen von Zeit- und Frequenzintegral ergibt sich: $${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot \int^{+\infty}_{-\infty}X_{\rm T}(f)\cdot \left[ \int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x_{\rm T}(t)\cdot {\rm e}^{{\rm j}2 \pi f t } \hspace{0.1cm} \rm d \it t \right] \cdot {\rm e}^{{\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f.$$ Das innere Integral beschreibt das konjugiert–komplexe Spektrum $X_{\rm T}^{\star}(f)$. Daraus folgt weiter: $${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot \int^{+\infty}_{-\infty}|X_{\rm T}(f)|^2 \cdot {\rm e}^{{\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f.$$ Ein Vergleich mit dem bei Ergodizität stets gültigen Theorem von Wiener und Chintchine, $${{\it \varphi}_x(\tau)} = \int^{+\infty}_{-\infty}{\it \Phi}_x(f) \cdot {\rm e}^{{\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f ,$$ zeigt die Gültigkeit der Beziehung: $${{\it \Phi}_x(f)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot |X_{\rm T}(f)|^2.$$
q.e.d.