Aufgabe 1.3: Fiktive Uni Irgendwo

• Zurück zum Buch

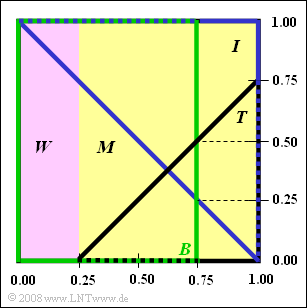
Aus nebenstehender Grafik können Sie einige Informationen über die FUI (Fiktive Universität Irgendwo) ablesen. Das gesamte Quadrat steht für die Grundmenge $G$ der 960 Studierenden. Von diesen sind

• 25% weiblich (Menge $W$, violettes Rechteck),

• 75% männlich (Menge $M$, gelbes Rechteck). An der Universität gibt es die Fakultäten für

• Theologie (Menge $T$, schwarzes Dreieck),

• Informationstechnik (Menge $I$, blaues Dreieck),

• Betriebswirtschaft (Menge $B$, grünes Viereck).

Jeder Studierende muss mindestens einer dieser Fakultäten zugeordnet sein, kann jedoch auch gleichzeitig zwei oder drei Fakultäten angehören.

Die Flächen in der obigen Darstellung sind maßstäblich, so dass Sie anhand der angegebenen Zahlenwerte und einfachen geometrischen Überlegungen die (prozentualen) Belegungszahlen leicht angeben können.

Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 1.2. Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo:

Fragebogen

1

Berechnen Sie die Anzahl der in den Fakultäten Immatrikulierten. Geben Sie zur Kontrolle die Studierendenzahl in der theologischen Fakultät ein.

$N_T$ =

2

Welche der nachfolgenden Aussagen sind zutreffend?

	$I$ ist eine Teilmenge von $M$.
	$W$ ist eine Teilmenge von $B$.
	$W$ und $M$ ergeben zusammen ein vollständiges System.
	$B$, $I$ und $T$ ergeben zusammen ein vollständiges System.
	$W$ und $T$ sind disjunkte Mengen.
	Die Vereinigungsmenge von $B$, $I$ und $T$ ergibt die Grundmenge.
	Die Schnittmenge von $B$, $I$ und $T$ ergibt die leere Menge.

3

Wie groß ist der IT-Studentinnen-Anteil bezogen auf alle Studierenden?

$Pr[IT-Studentin]$ =

4

Wie groß ist der Anteil der Studentinnen mit nur einem Studienfach?

$Pr[ein Studienfach]$ =

5

Wie groß ist der Anteil der Studierenden mit drei Studienfächern?

$Pr[drei Studienfach]$ =

6

Wie groß ist der Anteil der Studierenden mit zwei Studienfächern?

$Pr[zwei Studienfächer]$ =

Musterlösung

Musterlösung

1. 2. 3. 4. 5. 6. 7.