Aufgabe 1.8: Variable Flankensteilheit
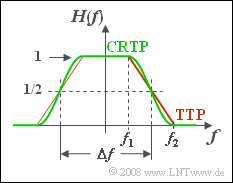
Zwei Tiefpässe mit variabler Flankensteilheit sollen miteinander verglichen werden. Für Frequenzen $|f| ≤ f_1$ gilt in beiden Fällen $H(f) =$ 1. Dagegen werden alle Frequenzen $|f| ≥ f_2$ vollständig unterdrückt.
Im mittleren Bereich $f_1 ≤ |f| ≤ f_2$ sind die Frequenzgänge durch die nachfolgenden Gleichungen festgelegt:
- Trapeztiefpass (TTP):
$$H(f) = \frac{f_2 - |f|}{f_2 - f_1} ,$$
- Cosinus–Rolloff–Tiefpass (CRTP):
$$H(f) = \cos^2 \left(\frac{|f|- f_1}{f_2 - f_1} \cdot\frac{\pi}{2} \right).$$
Alternative Systemparameter sind für beide Tiefpässe die über das flächengleiche Rechteck definierte äquivalente Bandbreite $Δf$ sowie der Rolloff–Faktor (im Frequenzbereich):
$$r=\frac{f_2 - f_1}{f_2 + f_1} .$$
In der gesamten Aufgabe gelte $Δf =$ 10 kHz und $r =$ 0.2. Die Impulsantworten lauten mit der äquivalenten Impulsdauer $Δt = 1/Δf =$ 0.1 ms:
$$h_{\rm TTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot
\frac{t}{\Delta t} )\cdot {\rm si}(\pi \cdot r \cdot \frac{t}{\Delta t} ),$$
$$h_{\rm CRTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot
\frac{t}{\Delta t} )\cdot \frac {\cos(\pi \cdot r \cdot t / \Delta
t )}{1 - (2 \cdot r \cdot t/\Delta t )^2}.$$
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.3. Sie können Ihre Ergebnisse mit folgendem Interaktionsmodul überprüfen:
Fragebogen
Musterlösung
- a)
- b)
- c)
- d)
- e)
- f)
- g)