Eigenschaften von Nyquistsystemen

Erstes Nyquistkriterium im Zeitbereich

Für dieses Kapitel wurde vorausgesetzt, dass die Detektion eines Symbols nicht durch Nachbarimpulse beeinträchtigt werden soll. Dies erreicht man durch die Detektion des Signals

\(d(t) = \sum \limits_{\it (\nu)} a_\nu \cdot g_d ( t - \nu T)\)

zu den Zeitpunkten νT immer dann, wenn der Detektionsgrundimpuls g_d(t)

auf den Bereich | t | < T beschränkt ist, was für das Kapitel 1.2 vorausgesetzt wurde, oder
äquidistante Nulldurchgänge zu den Zeitpunkten νT aufweist.

Aus Gründen einer möglichst einfachen Darstellung wird im Kapitel 1.3 das Detektionsstörsignal d_N(t) als vernachlässigbar klein angenommen.

: Man bezeichnet einen Detektionsgrundimpuls mit den Eigenschaften

\[g_d ( t = \nu T)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r}}\hspace{0.3cm} \nu = \pm 1, \pm 2,\pm 3,\hspace{0.05cm}...\]

als Nyquistimpuls g_Nyq(t), benannt nach dem Physiker Harry Nyquist.

: Die Grafik zeigt das Detektionssignal d(t) eines solchen Nyquistsystems. Rot gepunktet sind die (gewichteten und verschobenen) Nyquistimpulse a_ν · g_Nyq(t – νT) eingezeichnet.

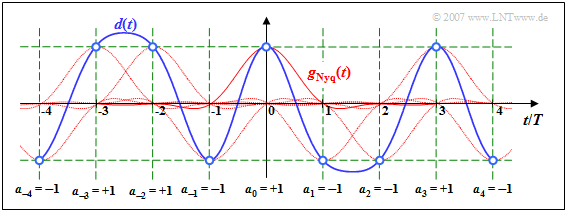
Zu den Detektionszeitpunkten gilt d(νT) = a_ν · g_Nyq(0), wie aus den blauen Kreisen und dem grünen Raster hervorgeht. Die Nachläufer der vorangegangenen Impulse (ν < 0) sowie die Vorläufer der nachfolgenden Impulse (ν > 0) beeinflussen beim Nyquistsystem die Detektion des Symbols a₀ nicht.

Der Vollständigkeit halber sei erwähnt, dass für diese Grafik der Detektionsgrundimpuls

\(g_{\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot T}\right)\)

mit trapezförmigem Spektrum und dem Rolloff–Faktor r = 0.5 zugrunde liegt. Dieser wurde bereits im Kapitel 3 des Buches „Signaldarstellung” behandelt.

Erstes Nyquistkriterium im Frequenzbereich

Harry Nyquist hat die Bedingung für eine impulsinterferenzfreie Detektion nicht nur für den Zeitbereich formuliert, sondern 1928 auch das entsprechende Kriterium im Frequenzbereich angegeben.
Erstes Nyquistkriterium: Erfüllt das Spektrum G_d(f) des Detektionsgrundimpulses die Bedingung

\(\sum \limits_{\it k = -\infty}^{+\infty} G_d \left ( f - \frac{k}{T} \right)= g_0 \cdot T = {\rm const.} \hspace{0.05cm}, \)

so ist g_d(t) ein Nyquistimpuls mit äquidistanten Nulldurchgängen zu den Zeitpunkten νT (ν ≠ 0) und der Amplitude g_d(t = 0) = g₀. Hinweis: Sie finden den Beweis auf Beweis des ersten Nyquistkriteriums.
Die nachfolgende Grafik zeigt zwei Nyquistspektren. Das Spektrum

\(G_1(f) = \left\{ \begin{array}{c} g_0 \cdot T \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} |f| < {1}/({2T})\hspace{0.05cm}, \\ |f| > {1}/({2T}) \hspace{0.1cm} \\ \end{array}\)

erfüllt offensichtlich die oben formulierte Bedingung und zwar mit der kleinstmöglichen Bandbreite. Der dazugehörige Nyquistimpuls g₁(t) = g₀ · si(πt/T) klingt sehr langsam ab, nämlich asymptotisch mit 1/t.

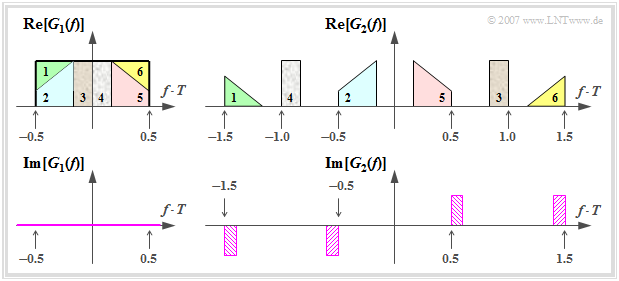
Der rechts oben dargestellte Realteil des Spektrums G₂(f) wurde aus dem Rechteckspektrum G₁(f) durch Verschiebung von Teilstücken um 1/T nach rechts oder links konstruiert. Wegen

\(\sum \limits_{\it k = -\infty}^{+\infty} {\rm Re}\left[G_2 \left ( f - \frac{k}{T} \right)\right]= g_0 \cdot T \hspace{0.05cm}, \hspace{1cm}\sum \limits_{\it k = -\infty}^{+\infty} {\rm Im}\left[G_2 \left ( f - \frac{k}{T} \right)\right]= 0\)

handelt es sich bei G₂(f) ebenfalls um ein Nyquistspektrum. Beim Imaginärteil heben sich die jeweils gleich schraffierten Anteile, die jeweils um 2/T auseinander liegen, auf. Die Angabe des dazugehörigen Nyquistimpulses g₂(t) ist allerdings sehr kompliziert.

Beweis des ersten Nyquistkriteriums

Wir gehen von der ersten Nyquistbedingung im Zeitbereich aus:\[g_{\rm Nyq}(\nu T) = \left\{ \begin{array}{c} g_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} \nu = 0 \hspace{0.05cm}, \\ \nu \ne 0 \hspace{0.1cm}. \\ \end{array}\]
Aus dem zweiten Fourierintegral erhält man somit für ν ≠ 0:\[g_{\rm Nyq}(\nu T) = \int_{-\infty}^{+\infty}G_{\rm Nyq}(f) \cdot {\rm e}^{ \hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi f \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.\]
Zerlegt man das Fourierintegral in Teilintegrale der Breite 1/T, so lauten die Bedingungsgleichungen:\[\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{(k-1/2)/T}^{(k+1/2)/T}G_{\rm Nyq}(f) \cdot {\rm e}^{ \hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi f \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.\]
Mit der Substitution f ' = f + k/T folgt daraus:\[\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{-1/(2T)}^{1/(2T)}G_{\rm Nyq}(f' - \frac{k}{T} ) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm} (f'- k/T) \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f ' = 0 \hspace{0.05cm}.\]
Für alle ganzzahligen Werte von k und ν gilt:\[{\rm e}^{-{\rm j} \hspace{0.05cm}2 \pi \hspace{0.05cm} k \hspace{0.05cm} \nu } = 1 \hspace{0.4cm} \Rightarrow \hspace{0.4cm}\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{-1/(2T)}^{1/(2T)}G_{\rm Nyq}(f' - \frac{k}{T} ) \cdot {\rm e}^{{\rm j} \hspace{0.05cm}2 \pi \hspace{0.02cm}f' \hspace{0.02cm} \nu \hspace{0.05cm}T}\,{\rm d} f ' = 0 \hspace{0.05cm}.\]
Durch Vertauschen von Summation und Integration sowie Umbenennen von

f ' in f folgt weiter:\[\int_{-1/(2T)}^{1/(2T)}\hspace{0.2cm} \sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) \cdot {\rm e}^{{\rm j} \hspace{0.05cm}2 \pi \hspace{0.02cm}f \hspace{0.02cm} \nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.\]

Diese Forderung ist für alle ν ≠ 0 nur dann zu erfüllen, wenn die unendliche Summe unabhängig von f ist, also einen konstanten Wert besitzt:\[\sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) = K_{\rm Nyq} \hspace{0.05cm}.\]
Aus der vorletzten Gleichung erhält man gleichzeitig für ν = 0:\[\int_{-1/(2T)}^{1/(2T)}\hspace{0.2cm} \sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) \,{\rm d} f = K_{\rm Nyq} \cdot \frac{1}{T} = g_0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}K_{\rm Nyq} = g_0 \cdot T \hspace{0.05cm}.\]
left(q.e.d)