Aufgabe 3.8: Nochmals Transinformation

Wir betrachten das Tupel $Z = (X, Y)$, wobei die Einzelkomponenten $X$ und $Y$ jeweils ternäre Zufallsgrößen darstellen:

$X = \{ 0 , 1 , 2 \}$ , $Y= \{ 0 , 1 , 2 \}$.

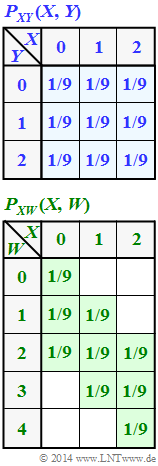
Die gemeinsame Wahrscheinlichkeitsfunktion $P_{ XY }(X, Y)$ beider Zufallsgrößen ist oben angegeben. In der Zusatzaufgabe Z3.7 wird diese Konstellation ausführlich analysiert. Man erhält als Ergebnis:

$H(X) = H(Y) = log_2 (3) = 1.585 bit$
$H(XY) = log_2 (9) = 3.170 bit$,
$I(X, Y) = 0$,
$H(Z) = H(XZ) = 3.170 bit$,
$I(X, Z) = 1.585 bit$

Desweiteren betrachten wir hier die Zufallsgröße $W = \{ 0, 1, 2, 3, 4 \}$, deren Eigenschaften sich aus der Verbundwahrscheinlichkeitsfunktion $P_{ XW }(X, W)$ nach der unteren Skizze ergeben. Die Wahrscheinlichkeiten in allen weiß hinterlegten Feldern sind jeweils $0$.

Gesucht ist in der vorliegenden Aufgabe die Transinformation

zwischen den Zufallsgrößen $X$ und $W \Rightarrow I(X; W)$,
zwischen den Zufallsgrößen $Z$ und $W ⇒ I(Z; W)$.

Hinweis: Die Aufgabe bezieht sich auf Kapitel 3.2

Fragebogen

Musterlösung

1. Mit $X = \{0, 1, 2\}$, $Y = \{0, 1, 2\}$ gilt $X + Y = \{0, 1, 2, 3, 4\}$ und auch die Wahrscheinlichkeiten stimmen mit der vorgegebenen Wahrscheinlichkeitsfunktion überein. Die Überprüfung der beiden anderen Vorgaben zeigt, dass auch $W = X – Y + 2$ möglich ist $\Rightarrow$ $Lösungsvorschläge 1$ und $2$.

2.Aus der 2D–Wahrscheinlichkeitsfunktion $P_{ XW }(X, W)$ auf der Angabenseite erhält man für

die Verbundentropie:

$$H(XW) = log_2(9) = 3.170$$,

die Wahrsacheinlichkeitsfunktion der Zufallsgröße $W$:

$$P_W(W) = [ 1/9 , 2/9 , 3/9 , 2/9 , 1/9]$$,

die Entropie der Zufallsgröße $W$:

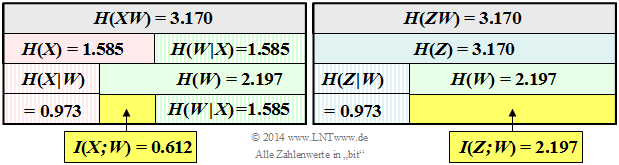
$$H(W) = 2 . \frac{1}{9} . log_2\frac{9}{1} + 2 . \frac{2}{9} . log_2\frac{9}{2} + 2 . \frac{3}{9} . log_2\frac{9}{3} = 2.197 ( bit)$$. Mit $H(X) = 1.585$ bit (wurde angegeben) ergibt sich somit für die Mutual Information: $$I(X;W) = H(X) + H(W) - H(XW)=$$ $$=1.585+2.197-3.170=0.612(bit)$$ Das linke Schaubild verdeutlicht die Berechnung der Transinformation $I(X; W)$ zwischen der ersten Komponente $X$ und der Summe $W$.

3.Die Grafik zeigt die Verbundwahrscheinlichkeit $P_{ ZW }(⋅)$. Das Schema besteht aus $5 · 9 = 45$ Feldern im Gegensatz zur Darstellung von $P_{ XW }(⋅)$ auf der Angabenseite mit $3 · 9 = 27$ Feldern.

Von den $45$ Feldern sind aber auch nur neun mit Wahrscheinlichkeiten $≠ 0$ belegt. Für die Verbundentropie gilt:

$H(ZW) = 3.170(bit)$

Mit den weiteren Entropien

$$H(Z) = 3.170 (bit)$$ $$H(W) = 2.197 (bit)$$ entsprechend der Aufgabe Z3.7 bzw. der Teilaufgabe (b) erhält man für die Transinformation:

$$I(Z;W) = H(Z) + H(W) - H(ZW) = 2.197 (bit)$$ wie auch aus dem rechten oberen Schaubild hervorgeht.

4. $Alle drei Aussagen$ treffen zu, wie auch aus dem oberen Schaubild ersichtlich ist. Wir versuchen eine Interpretation dieser numerischen Ergebnisse:

Die Verbundwahrscheinlichkeit $P_{ ZW }$ setzt sich ebenso wie $P_{ XW }$ aus neun gleichwahrscheinlichen Elementen $≠ 0$ zusammen. Damit ist offensichtlich, dass auch die Verbundentropien gleich sind:

$H(ZW) = H(XW) = 3.170 (bit)$.

Wenn ich das Tupel $Z = (X, Y)$ kenne, kenne ich natürlich auch die Summe $W = X + Y$. Damit ist $H(W|Z) = 0$. Dagegen ist $H(Z|W)$ ungleich $0$. Vielmehr gilt $H(Z|W) = H(X|W) = 0.973 bit$.
Die Zufallsgröße $W$ liefert also die genau gleiche Information hinsichtlich des Tupels $Z$ wie für die Einzelkomponente $X$. Dies ist die verbale Interpretation für die Aussage $H(Z|W) = H(X|W)$
Die gemeinsame Information von $Z$ und $W \Rightarrow I(Z; W)$ ist größer als die von $X und W \Rightarrow I(X; W)$, weil $H(W|Z)$ gleich $0$ ist, während $H(W|X)$ ungleich $0$ ist, nämlich genau so groß ist wie $H(X)$ :

$$I(Z;W) = H(W) - H(W|Z) = 2.197 - 0 = 2.197 (bit)$$ $$I(X;W) = H(W) - H(W|X) = 2.197 - 1.585 = 0.612 (bit)$$