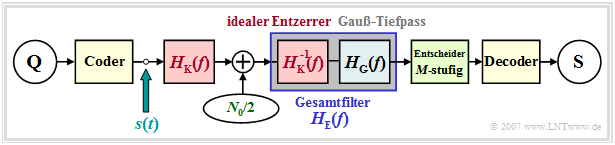
Impulsinterferenzen bei mehrstufiger Übertragung

Augenöffnung bei redundanzfreien Mehrstufensystemen (1)

Wir gehen weiterhin von folgenden Voraussetzungen aus:

NRZ–Rechteck–Sendeimpulse,

Koaxialkabel und AWGN–Rauschen,

ideale Kanalentzerrung, sowie

ein Gaußtiefpass zur Rauschleistungsbegrenzung.

Im Unterschied zu Kapitel 3.3 ist das weiterhin redundanzfreie Sendesignal s(t) nun nicht mehr binär, sondern M–stufig, was sich nur im Wertevorrat der Amplitudenkoeffizienten auswirkt:

\[s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.3cm}{\rm mit}\hspace{0.3cm} a_\nu \in \{ a_1, ... , a_\mu , ... , a_{M}\}\hspace{0.05cm}.\]

Dementsprechend besitzt der Entscheider nun nicht mehr nur eine, sondern M – 1 Entscheiderschwellen und im Augendiagramm sind bei geöffnetem Auge M – 1 Augenöffnungen erkennbar.

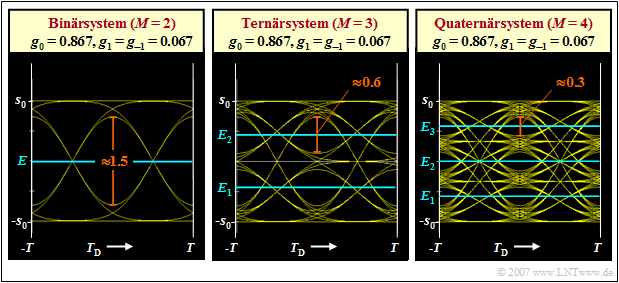
Vergleicht man die Augendiagramme (ohne Rauschen)

eines binären (M = 2),

eines ternären (M = 3), und

eines quaternären (M = 4)

Übertragungssystems bei gleichem vorgegebenen Detektionsgrundimpuls g_d(t) und gleicher Symboldauer T, so erhält man für die halbe vertikale Augenöffnung allgemein:

\[{\ddot{o}(T_{\rm D})}/{ 2} = \frac{g_0}{ M-1} - \sum_{\nu = 1}^{\infty} |g_{-\nu} | - \sum_{\nu = 1}^{\infty} |g_{\nu} |\hspace{0.05cm}.\]

Hierbei bezeichnet g₀ = g_d(t = 0) wie im Kapitel 3.3 den Hauptwert, während die beiden Summen in obiger Gleichung

die Vorläufer g₁, g₂, ... (zweiter Term), und
die Nachläufer g_–1, g_–2, ... (dritter Term)

berücksichtigen. Dabei gilt stets g_ν = g_d(t = ν · T).

Auf der nächsten Seite wird diese Gleichung an einem Beispiel verdeutlicht.

Augenöffnung bei redundanzfreien Mehrstufensystemen (2)

: Nachfolgend sehen Sie drei Augendiagramme für die Stufenzahlen M = 2, M = 3 und M = 4. Das binäre Augendiagramm gilt für einen Gaußtiefpass mit der Grenzfrequenz f_G · T ≈ 0.6. Mit dem Hauptwert g₀ = 0.867 · s₀ und den beiden Ausläufern g_–1 = g₁ = 0.067 · s₀ ergibt sich in diesem Fall für die vertikale Augenöffnung (Rundung auf eine Nachkommastelle):

\[{\ddot{o}(T_{\rm D})}= 2 \cdot (g_0 - 2 \cdot g_1) \approx 1.5 \cdot s_0 \hspace{0.05cm}.\]

Bei den Mehrstufensystemen ist die Augenöffnung per se um den Faktor 1/(M – 1) kleiner. Dadurch wird hier die Augenöffnung durch die (gleich großen) Vor– und Nachläufer (relativ gesehen) stärker verringert als beim Binärsystem. Man erhält bei gleichen Grundimpulswerten für

\[M = 3 : \hspace{0.2cm}{\ddot{o}(T_{\rm D})} = 2 \cdot (g_0/2 - 2 \cdot g_1) \approx 0.6 \cdot s_0 \hspace{0.05cm},\] \[ M = 4 : \hspace{0.2cm}{\ddot{o}(T_{\rm D})} = 2 \cdot (g_0/3 - 2 \cdot g_1) \approx 0.3 \cdot s_0 \hspace{0.05cm}.\]

Anzumerken ist, dass auch für diese beiden Mehrstufensysteme jeweils die normierte Grenzfrequenz <nobr>f_G · T = 0.6</nobr> zugrundeliegt. Bei einem Systemvergleich ist allerdings zu beachten, dass sich durch die größere Stufenzahl auch der Informationsfluss erhöht. Das heißt, dass die Mehrstufensysteme besser sind, als es diese Grafiken aussagen. Mehr darüber auf der nächsten Seite.