Das GWSSUS–Kanalmodell

1. Mobile Kommunikation
2. Frequenzselektive Übertragungskanäle
3. Das GWSSUS–Kanalmodell

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Verallgemeinerte Systemfunktionen zeitvarianter Systeme (1)

Während es bei linearen zeitinvarianten (LZI) Systemen mit der Übertragungsfunktion H(f) und der Impulsantwort h(τ) nur zwei das System vollständig beschreibende Funktionen gibt, sind bei zeitvarianten (LZV) Systemen insgesamt vier verschiedene Systemfunktionen möglich. Eine formale Untersscheidung dieser Funktionen hinsichtlich Zeit– und Frequenzbereichsdarstellung durch Klein– und Großbuchstaben ist damit ausgeschlossen.

Deshalb nehmen wir nun eine Nomenklaturänderung vor, die sich wie folgt formalisieren lässt:

• Die vier möglichen Systemfunktionen werden einheitlich mit η₁₂ bezeichnet.
  

• Der erste Index ist entweder ein V (Verzögerungszeit τ) oder ein F (Frequenz f).
  

• Als zweiter Index ist entweder ein Z (Zeit t) oder ein D (Dopplerfrequenz f_D) möglich.
  
  

Da beim Mobilfunk im Gegensatz zur leitungsgebundenen Übertragung die Systemfunktionen nicht deterministisch beschrieben werden können, sondern statistische Größen sind, müssen später noch entsprechende Korrelationsfunktionen betrachtet werden. Diese bezeichnen wir im Folgenden einheitlich mit φ₁₂, und verwenden gleiche Indizes wie für die Systemfunktionen η₁₂.

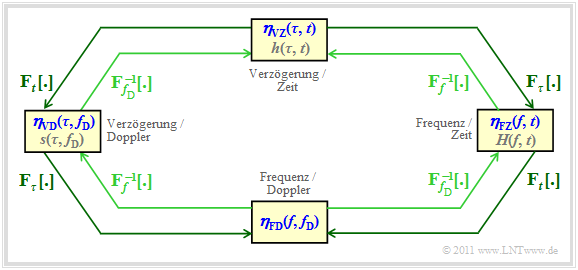
Diese formalisierten Bezeichnungen sind in der folgenden Grafik in blauer Schrift eingetragen. Zusätzlich sind die in anderen Kapiteln oder der Literatur verwendeten Bezeichnungen angegeben (graue Schrift). In den weiteren Kapiteln werden diese teilweise ebenfalls benutzt.

Die Bildbeschreibung folgt auf der nächsten Seite.

Verallgemeinerte Systemfunktionen zeitvarianter Systeme (2)

In der Grafik auf der letzten Seite sind die vier Systemfunktionen dargestellt. Oben erkennt man die zeitvariante Impulsantwort η_VZ(τ, t), die in Kapitel 2.2 mit h(τ, t) bezeichnet wurde. Die zugehörige Autokorrelationsfunktion (AKF) ist

\[\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1, t_1) \cdot \eta_{\rm VZ}^{\star}(\tau_2, t_2) \right ]\hspace{0.05cm}. \]

Zur Frequenz–Zeit–Darstellung (rechter Block) kommt man durch eine Fouriertransformation bezüglich der Verzögerung τ. Man erhält so die zeitvariante Übertragungsfunktion H(f, t) = η_FZ(f, t). Die Fouriertransformation hinsichtlich τ ist in der Grafik durch „F_τ[ · ]” angedeutet. Ausgeschrieben lautet das Fourierintegral:

\[\eta_{\rm FZ}(f, t) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau, t) \cdot {\rm exp}(- {\rm j}\cdot 2 \pi f \tau)\hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}, \hspace{0.3cm} {\rm kurz:} \hspace{0.2cm} \eta_{\rm FZ}(f, t) \hspace{0.2cm} \stackrel{f, \hspace{0.05cm} \tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t) \hspace{0.05cm}.\]

Die AKF dieser zeitvarianten Übertragungsfunktion lautet allgemein:

\[\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) = {\rm E} \left [ \eta_{\rm FZ}(f_1, t_1) \cdot \eta_{\rm FZ}^{\star}(f_2, t_2) \right ]\hspace{0.05cm}.\]

Die Scatter–Funktion η_VD(τ, f_D) entsprechend dem linken Block – manchmal auch mit s(τ, f_D) bezeichnet – beschreibt den Mobilfunkkanal im Verzögerungs–Doppler–Bereich. Sie ergibt sich aus der zeitvarianten Impulsantwort η_VZ(τ, t) durch Fouriertransformation bezüglich des zweiten Parameters t:

\[ \eta_{\rm VD}(\tau, f_{\rm D}) \hspace{0.2cm} \stackrel{f_{\rm D}, \hspace{0.05cm}t}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t)\]

\[\Rightarrow \hspace{0.3cm} \varphi_{\rm VD}(\tau_1, f_{\rm D_1}, \tau_2, f_{\rm D_2}) = {\rm E} \left [ \eta_{\rm VD}(\tau_1, f_{\rm D_1}) \cdot \eta_{\rm VD}^{\star}(\tau_2, f_{\rm D_2}) \right ] \hspace{0.05cm}.\]

Der Funktionsparameter f_D bezeichnet hierbei die Dopplerfrequenz.

Abschließend betrachten wir noch die so genannte frequenzvariante Übertragungsfunktion, also die Frequenz–Doppler–Darstellung. Entsprechend der Grafik gelangt man zu dieser auf zwei Wege:

\[\eta_{\rm FD}(f, f_{\rm D}) \hspace{0.2cm} \stackrel{f_{\rm D}, \hspace{0.05cm}t}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm FZ}(f, t)\hspace{0.05cm},\]

\[\eta_{\rm FD}(f, f_{\rm D}) \hspace{0.2cm} \stackrel{f, \hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VD}(\tau, f_{\rm D})\hspace{0.05cm}.\]

Anzumerken ist, dass die angegebenen Fourier–Zusammenhänge zwischen den Systemfunktionen in der Grafik durch die äußeren, dunkelgrünen Pfeile veranschaulicht sind. Die inneren (helleren) Pfeile kennzeichnen jeweils die Verknüpfungen über die inverse Fouriertransformation.

Hinweis: Ein Interaktionsmodul zeigt den Zusammenhang zwischen Zeit– und Frequenzbereich, formelmäßig beschreibbar durch Fouriertransformation und Fourierrücktransformation:

Zeitfunktion und zugehörige Spektralfunktion Please add link and do not upload flash video.

Vereinfachungen aufgrund der GWSSUS–Voraussetzungen

Der allgemeine Zusammenhang zwischen den vier Systemfunktionen ist aufgrund nichtstationärer Effekte sehr kompliziert. Es müssen gegenüber dem allgemeinen Modell einige Einschränkungen getroffen werden, um zu einem geeigneten Modell für den Mobilfunkkanal zu gelangen, aus dem sich relevante Aussagen für praktische Anwendungen ableiten lassen.

Man kommt zum GWSSUS–Modell (Gaussian Wide Sense Stationary Uncorrelated Scattering) durch folgende Festlegungen:

• Der Zufallsprozess der Kanalimpulsantwort h(τ, t) = η_VZ(τ, t) wird allgemein als komplex (also Beschreibung im äquivalenten Tiefpassbereich), gaußisch (Kennung G) sowie als mittelwertfrei (Rayleigh, nicht Rice, also keine Sichtverbindung) angenommen.
  

• Der Zufallsprozess sei schwach stationär, das heißt, seine Kenngrößen ändern sich mit der Zeit nur geringfügig, und die AKF φ_VZ(τ₁, t₁, τ₂, t₂) der zeitvarianten Impulsantwort hängt nicht mehr von den absoluten Zeiten t₁ und t₂ ab, sondern nur noch von der Zeitdifferenz Δt = t₂ – t₁. Darauf weist die Kennung WSS   ⇒   Wide Sense Stationary hin.
  

• Die einzelnen Echos aufgrund von Mehrwegeausbreitung sind unkorreliert, was durch die Kennung US   ⇒   Uncorrelated Scattering ausgedrückt wird.
  

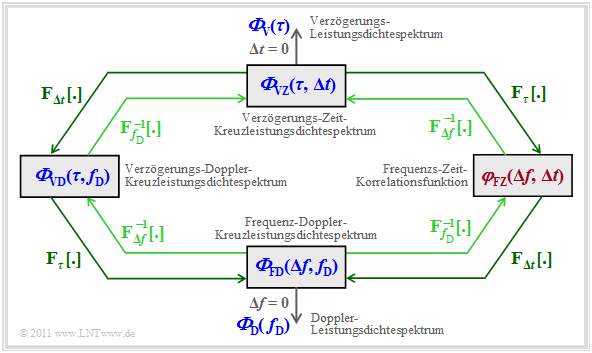
Unter Berücksichtigung dieser Eigenschaften lässt sich der Mobilfunkkanal entsprechend der hier angegebenen Grafik beschreiben. Auf die einzelnen Leistungsdichtespektren (blau beschriftet) und die Korrelationsfunktion (mit roter Schrift) wird auf den nächsten Seiten noch im Detail eingegangen.

AKF und LDS der zeitvarianten Impulsantwort (1)

Zunächst betrachten wir die Autokorrelationsfunktion (AKF) der zeitvarianten Impulsantwort  ⇒  h(τ, t) = η_VZ(τ, t) etwas genauer. Dabei zeigt sich:

• Aufgrund der WSS–Eigenschaft lässt sich mit Δt = t₂ – t₁ schreiben:

\[\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = \varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t)\hspace{0.05cm}.\]

• Da die Echos als unabhängig voneinander vorausgesetzt wurden (US–Eigenschaft), kann man die Impulsantwort bezüglich den Verzögerungen τ₁, τ₂ als unkorreliert annehmen. Dann gilt:

\[\varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t) = 0 \hspace{0.35cm}{\rm f\ddot{u}r}\hspace{0.35cm} \tau_1 \ne \tau_2\hspace{0.05cm}. \]

• Ersetzt man nun τ₁ durch τ und τ₂ durch τ + Δτ, so lässt sich diese Autokorrelationsfunktion in folgender Weise darstellen:

\[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}. \]

• Wegen der Ausblendeigenschaft der Diracfunktion verschwindet die AKF für τ₁ ≠ τ₂  ⇒  Δt ≠ 0. Φ_VZ(τ, Δt) nennt man das Verzögerungs–Zeit–Kreuzleistungsdichtespektrum, das von der Verzögerung τ (= τ₁ = τ₂) und zusätzlich von der Zeitdifferenz Δt = t₁ – t₂ abhängt.
  
  

Beachten Sie, dass hier Autokorrelationsfunktion φ_VZ(Δτ, Δt) und Leistungsdichtespektrum Φ_VZ(τ, Δt) nicht wie sonst üblich über die Fouriertransformation zusammenhängen, sondern nach obiger Gleichung über eine Diracfunktion verknüpft sind. Nicht alle Symmetrieeigenschaften, die aus dem Wiener–Chintchine–Theorem folgen, sind somit auch hier gegeben. Insbesondere ist es durchaus möglich und sogar sehr wahrscheinlich, dass ein solches Leistungsdichtespektrum eine ungerade Funktion ist.

In der Übersicht ist das Verzögerungs–Zeit–Kreuzleistungsdichtespektrum Φ_VZ(τ, Δt) oben in der Mitte zu erkennen. Da η_VZ(τ, t) wie jede beliebige Impulsantwort die Einheit [1/s] aufweist, hat die Autokorrelationsfunktion

\[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = {\rm E} \left [ \eta_{\rm VZ}(\tau, t) \cdot \eta_{\rm VZ}^{\star}(\tau + \Delta \tau, t + \Delta t) \right ]\]

die Einheit [1/s²]. Da aber auch die Diracfunktion mit Zeitargument, δ(Δτ), die Einheit [1/s] aufweist, besitzt das Verzögerungs–Zeit–Kreuzleistungsdichtespektrum Φ_VZ(τ, Δt) ebenfalls die Einheit [1/s]:

\[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}.\]

AKF und LDS der zeitvarianten Impulsantwort (2)

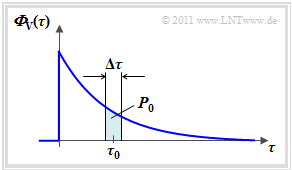
Zum Verzögerungs–Leistungsdichtespektrum Φ_V(τ) kommt man, indem man in der Funktion Φ_VZ(τ, Δt) den zweiten Parameter Δt = 0 setzt. Die Grafik zeigt einen beispielhaften Verlauf.

Das Verzögerungs–Leistungsdichtespektrum Φ_V(τ) ist eine zentrale Größe für die Beschreibung eines Mobilfunkkanals. Es weist folgende Eigenschaften auf:

• Φ_V(τ₀) ist ein Maß für die „Leistung” derjenigen Signalanteile, die um τ₀ verzögert werden. Es wird hierfür implizit eine Mittelung über alle Dopplerfrequenzen (f_D) vorgenommen.
  

• Das Verzögerungs–Leistungsdichtespektrum Φ_V(τ) hat wie Φ_VZ(τ, Δt) die Einheit [1/s]. Es charakterisiert die Leistungsverteilung über alle möglichen Verzögerungszeiten τ.
  

• In obiger Grafik farblich markiert ist die Leistung P₀ ≈ Φ_V(τ₀) · Δτ solcher Signalanteile, die beim Empfänger über beliebige Pfade mit einer Verzögerung zwischen τ₀ ± Δτ/2 eintreffen.
  

• Normiert man das Leistungsdichtespektrum Φ_V(τ) derart, dass sich die Fläche 1 ergibt, so erhält man die Wahrscheinlichkeitsdichtefunktion (WDF) der Verzögerungszeit:

\[{\rm WDF}_{\rm V}(\tau) = \frac{{\it \Phi}_{\rm V}(\tau)}{\int_{0 }^{\infty}{\it \Phi}_{\rm V}(\tau)\hspace{0.15cm}{\rm d}\tau} \hspace{0.05cm}.\]

Im Buch „Stochastische Signaltheorie” hätten wir diese Wahrscheinlichkeitsdichtefunktion mit f_τ(τ) bezeichnet. Um den Zusammenhang zwischen Φ_V(τ) und der WDF deutlich werden zu lassen und Verwechslungen mit der Frequenz f zu vermeiden, wurde hier diese Nomenklatur gewählt.

Verzögerungsmodelle nach COST 207

In den 1990er Jahren gründete die Europäische Union die Arbeitsgruppe COST 207 mit dem Ziel, standardisierte Kanalmodelle für den zellularen Mobilfunk bereitzustellen. Hierbei steht COST für European Cooperation in Science and Technology.

In diesem internationalen Gremium wurden vier Profile für die Verzögerungszeit τ entwickelt, basierend auf Messungen und gültig für unterschiedliche Anwendungsszenarien. Im Folgenden werden vier verschiedene Verzögerungs–Leistungsdichtespektren angegeben, wobei stets der Normierungsfaktor Φ₀ = Φ_V(τ = 0) verwendet wird:

• Profil RA (englisch Rural Area)   ⇒   ländliches Gebiet:

\[{{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.15cm}{\rm im \hspace{0.15cm}Bereich}\hspace{0.15cm} 0 < \tau < 0.7\,{\rm \mu s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.109\,{\rm \mu s}\hspace{0.05cm}.\]

• Profil TU (englisch Typical Urban)   ⇒   Städte und Vororte:

\[{{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.15cm}{\rm im \hspace{0.15cm}Bereich}\hspace{0.15cm} 0 < \tau < 7\,{\rm \mu s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm \mu s}\hspace{0.05cm}.\]

• Profil BU (englisch Bad Urban)   ⇒   ungünstige Bedingungen in Städten:

\[{{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ 0.5 \cdot {\rm e}^{ (5\,{\rm \mu s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}l} \hspace{-0.05cm} {\rm im \hspace{0.15cm}Bereich}\hspace{0.15cm} 0 < \tau < 5\,{\rm \mu s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm \mu s}\hspace{0.05cm}, \\ \hspace{-0.05cm} {\rm im \hspace{0.15cm}Bereich}\hspace{0.15cm} 5\,{\rm \mu s} < \tau < 10\,{\rm \mu s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm \mu s} \hspace{0.05cm}. \\ \end{array}\]

• Profil HT (englisch Hilly Terrain)   ⇒   hügeliges Gebiet und Bergland:

\[{{\it \Phi}_{\rm V}(\tau)}/{\it \Phi}_{\rm 0} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ 0.04 \cdot {\rm e}^{ (15\,{\rm \mu s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}l} \hspace{-0.4cm} {\rm im \hspace{0.15cm}Bereich}\hspace{0.15cm} 0 < \tau < 2\,{\rm \mu s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.286\,{\rm \mu s}\hspace{0.05cm}, \\ \hspace{-0.4cm} {\rm im \hspace{0.15cm}Bereich}\hspace{0.15cm} 15\,{\rm \mu s} < \tau < 20\,{\rm \mu s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm \mu s} \hspace{0.05cm}. \\ \end{array}\]

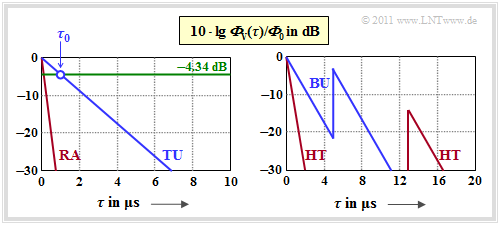
Die Grafik zeigt die Verzögerungs–Leistungsdichte dieser Profile in logarithmischer Darstellung. Aus den Exponentialfunktionen bei linearer Darstellung werden nun geradlinige Verläufe.

Bei dieser logarithmischen Darstellung kann man den LDS–Parameter τ₀ bei 10 &middot lg(1/e) = –4.34 dB ablesen, wie in der Grafik für das TU-Profil eingezeichnet. Auf diese vier COST–Profile wird in der Aufgabe A2.8 noch genauer eingegangen.