Beispiele binärer Blockcodes
Inhaltsverzeichnis
Single Parity–check Codes (1)
Der Single Parity–check Code (SPC) fügt zu dem Informationsblock u = (u1, u2, ... , uk) ein Prüfbit (englisch: Parity) p hinzu:
\[\underline{u} = (u_1, u_2,\hspace{0.05cm} ... \hspace{0.05cm} , u_k) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x} = (x_1, x_2,\hspace{0.05cm} ... \hspace{0.05cm} , x_n) = (u_1, u_2,\hspace{0.05cm} ... \hspace{0.05cm} , u_k, p) \hspace{0.05cm}.\]
Die Grafik zeigt drei Beispiele solcher Codes mit |C| = 4 (k = 2), |C| = 8 (k = 3) und |C| = 16 (k = 4).
Dieser sehr einfache Code ist wie folgt charakterisiert:
- Aus n = k + 1 folgt für die Coderate R = k/n = (n – 1)/n und für die Redundanz 1 – R = 1/n. Für k = 2 ergibt sich zum Beispiel die Coderate 2/3 und die relative Redundanz beträgt 33.3%.
- Das Prüfbit erhält man durch die Modulo–2–Addition. Darunter versteht man die Addition im Galoisfeld zur Basis 2 ⇒ GF(2), sodass 1⊕1 = 0 ergibt:
- \[p = u_1 \oplus u_2 \oplus ... \hspace{0.05cm} \oplus u_k \hspace{0.05cm}.\]
- Damit enthält jedes gültige Codewort x eine gerade Anzahl von Einsen. Ausgedrückt mit ⊕ bzw. in vereinfachter Schreibweise entsprechend der zweiten Gleichung lautet diese Bedingung:
- \[ x_1 \oplus x_2 \oplus ... \hspace{0.05cm} \oplus x_n = 0 \hspace{0.05cm}, \hspace{0.5cm}{\rm oder:}\hspace{0.15cm} \sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} , \hspace{0.3cm} {\rm Addition\hspace{0.15cm} in \hspace{0.15cm} GF(2)} \hspace{0.05cm}. \]
- Für k = 2 ⇒ n = 3 ergeben sich die folgenden vier Codeworte, wobei in der ersten Zeile das Prüfbit jeweils durch einen kleinen Pfeil markiert ist:
- \[\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\]
- Es handelt sich um einen linearen Code, da die Summe zweier beliebiger Codeworte wieder ein gültiges Codewort ergibt, zum Beispiel x1 ⊕ x2 = x3.
- Für beliebiges k ⇒ n = k + 1 unterscheidet sich jedes Codewort von allen anderen an einer geraden Anzahl von Positionen. Bei diesem Code ist die minimale Distanz dmin = 2.
Mit der allgemeinen Codebezeichnung (n, k, dmin) lässt sich jeder Single Parity–check Code auch mit (n, n – 1, 2) benennen. Die Grafik zeigt den SPC (3, 2, 2), den SPC (4, 3, 2) und den SPC (5, 4, 2).
Single Parity–check Codes (2)
Der digitale Kanal ändert möglicherweise das Codewort x = (x1, x2, ... , xn) in das Empfangswort y = (y1, y2, ... , yn), wobei mit dem Fehlervektor e = (e1, e2, ... , en) gilt: y = x ⊕ e. Zur Decodierung des Single Parity–check Codes bildet man das sogenannte Syndrom:
\[s = y_1 \oplus y_2 \oplus ... \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} \hspace{0.05cm}.\]
Das Ergebnis „s = 1” weist dann auf (mindestens) einen Bitfehler innerhalb des Codewortes hin, während „s = 0” wie folgt zu interpretieren ist:
- Die Übertragung war fehlerfrei, oder:
- Die Anzahl der Bitfehler ist geradzahlig.
Für das BSC–Modell mit ε = 1% ergeben sich dann folgende Wahrscheinlichkeiten:
- Das Informationswort wird richtig decodiert (blaue Hinterlegung):
- \[{\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.\]
- Der Decoder erkennt, dass Übertragungsfehler aufgetreten sind (grüne Hinterlegung):
- \[{\rm Pr}(s=1) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=1 \atop f \hspace{0.1cm}{\rm ungerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = \]
- \[\hspace{1.8cm} = \hspace{-0.1cm} {4 \choose 1} \cdot 0.01 \cdot 0.99^3 + {4 \choose 3} \cdot 0.01^3 \cdot 0.99 \approx 3.9\,\%\hspace{0.05cm}.\]
- Das Informationswort wird falsch decodiert (rote Hinterlegung):
- \[{\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = \]
- \[\hspace{2cm} = \hspace{-0.1cm} 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.\]
In der Aufgabe A1.5 werden die hier gewonnenen Ergebnisse noch ausführlich diskutiert.
Single Parity–check Codes (3)
Eine Fehlerkorrektur des Single Parity–check Codes ist beim BSC–Modell nicht möglich im Unterschied zum BEC–Kanal (Binary Erasure Channel). Bei diesem werden Bitfehler ausgeschlossen. Ist nur ein Bit ausgelöscht (englisch: Erasure, E), so ist aufgrund der Tatsache „die Anzahl der Einsen im Codewort ist gerade” auch eine Fehlerkorrektur möglich, zum Beispiel für den SPC (5, 4):
\[\underline{y} \hspace{-0.1cm} = \hspace{-0.1cm} (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (1, 0, 1, 1) = \underline{u}\hspace{0.05cm},\] \[\underline{y} \hspace{-0.1cm} = \hspace{-0.1cm} (0, 1, 1, {\rm E}, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 1, 0, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 1, 0) = \underline{u}\hspace{0.05cm},\] \[\underline{y} \hspace{-0.1cm} = \hspace{-0.1cm} (0, 1, 0, 1, {\rm E}) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 0, 1, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 0, 1) = \underline{u}\hspace{0.05cm}.\]
Auch beim AWGN–Kanal ist Fehlerkorrektur möglich, wenn man Soft Decision anwendet. Für das Folgende gehen wir von bipolarer Signalisierung aus: x = 0 → x̃ = +1, x = 1 → x̃ = –1.
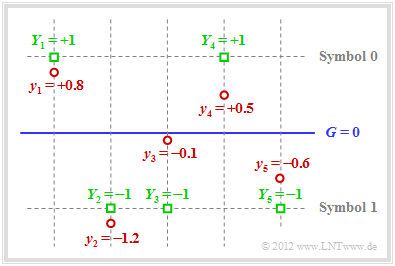
Die Grafik verdeutlicht den hier dargelegten Sachverhalt:
- Beispielsweise lautet der Empfangsvektor (rote Punkte):
- \[\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.\]
- Bei harter Entscheidung (Schwelle G = 0, nur die Vorzeichen werden ausgewertet) würde man zu folgendem binären Ergebnis kommen (grüne Quadrate Yi = yi / |yi|):
- \[\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.\]
- In Symbolschreibweise ergibt sich daraus (0, 1, 1, 0, 1), was kein gültiges Codewort ist ⇒ Syndrom s = 1. Also müssen ein, drei oder fünf Bit verfälscht worden sein.
- Die Wahrscheinlichkeit für drei oder fünf Bitfehler ist allerdings um Größenordnungen kleiner als diejenige für einen einzigen Fehler. Die Annahme „ein Bitfehler” ist deshalb nicht abwegig.
- Da der Empfangswert y3 sehr nahe an der Schwelle G = 0 liegt, geht man davon aus, dass genau dieses Bit verfälscht wurde. Damit fällt bei Soft Decision die Entscheidung für z = (0, 1, 0, 0, 1) ⇒ υ = (0, 1, 0, 0). Die Blockfehlerwahrscheinlichkeit Pr(υ ≠ u) ist so am geringsten.
Wiederholungscodes (1)
\[\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n): x_i = x_j \hspace{0.15cm}{\rm f\ddot{u}r \hspace{0.15cm}alle\hspace{0.25cm}} i, j = 1, ... \hspace{0.1cm}, n \}\]
als Wiederholungscode (englisch: Repetition Code, RC) der Länge n. Es gilt also stets k = 1. Entsprechend existieren nur zwei Codeworte (0, 0, ... , 0) und (1, 1, ... , 1), die sich in n Binärstellen unterscheiden. Daraus folgt für die minimale Distanz dmin = n.
Ein solcher (n, 1, n)–Blockcode besitzt nur die sehr kleine Coderate <nobr>R = 1/n,</nobr> ist aber auch sehr robust. Insbesondere beim BEC–Kanal genügt ein einziges richtig übertragenes Bit an beliebiger Position (alle anderen Bit können ausgelöscht sein), um das Informationswort richtig zu decodieren.
Betrachten wir zunächst die Decodierung und Fehlerwahrscheinlichkeiten beim BSC–Kanal.
\[{\rm Pr}(v = u) = \sum_{f=0 }^{(n-1)/2} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} \hspace{0.05cm}.\]
Die nachfolgenden Zahlenwerte gelten für n = 5. Das heißt: Es sind t = 2 Bitfehler korrigierbar:
\[{\rm Pr}(v = u) = (1 - \varepsilon)^5 + 5 \cdot \varepsilon \cdot (1 - \varepsilon)^4 + 10 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^3 \approx 99.15\,\%\]
\[\Rightarrow\hspace{0.3cm}{\rm Pr}(v \ne u) = 1- {\rm Pr}(v = u) \approx 0.85\,\%\hspace{0.05cm}.\]
Bei geradem n können dagegen nur n/2 – 1 Fehler korrigiert werden. Erhöht man n von 5 auf 6, so sind weiterhin auch nur zwei Bitfehler innerhalb eines Codewortes korrigierbar. Einen dritten Bitfehler kann man zwar nicht korrigieren, aber zumindest erkennen:
\[{\rm Pr}({\rm nicht\hspace{0.15cm} korrigierbarer\hspace{0.15cm} Fehler}) = {6 \choose 3} \cdot \varepsilon^{3} \cdot (1 - \varepsilon)^{3}= 20 \cdot 0.1^{3} \cdot 0.9^{3}\approx 1.46\,\%\hspace{0.05cm}. \]
Ein (unerkannter) Decodierfehler (υ ≠ u) ergibt sich erst, wenn innerhalb des 6 Bit–Wortes vier oder mehr Bit verfälscht wurden. Als Näherung unter der Annahme, dass fünf oder sechs Bitfehler sehr viel unwahrscheinlicher sind als vier, gilt:
\[{\rm Pr}(v \ne u) \approx {6 \choose 4} \cdot \varepsilon^{4} \cdot (1 - \varepsilon)^{2}= 0.122\,\%\hspace{0.05cm}.\]
Interessant ist, dass beim RC(6, 1, 6) die Wahrscheinlichkeit Pr(υ = u) für eine mögliche und richtige Decodierung mit 98.42% kleiner ist als beim RC(5, 1, 5).
Wiederholungscodes (2)
Nun interessieren wir uns für die Leistungsfähigkeit des Wiederholungscodes beim AWGN–Kanal. Bei uncodierter Übertragung (oder dem Wiederholungscode mit n = 1) ist der Empfangswert y = x̃ + η, wobei x̃ ∈ {+1, –1} das Informationsbit bei bipolarer Signalisierung bezeichnet und η den Rauschterm. Um Verwechslungen mit dem Codeparameter n zu vermeiden, wurde das Rauschen umbenannt: n → η.
Für die Fehlerwahrscheinlichkeit gilt mit dem komplementären Gaußschen Fehlerintegral Q(x)
\[{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{\rho}) \hspace{0.05cm},\]
wobei folgende physikalische Größen zu verwenden sind:
- das Signal–zu–Rauschleistungsverhältnis ρ = 1/σ2 = 2 ES/N0,
- die Energie ES pro Codesymbol ⇒ Symbolenergie,
- die normierte Streuung σ des Rauschens, gültig für das Nutzsignal x̃ ∈ {+1, –1}, und
- die konstante (einseitige) Rauschleistungsdichte N0 des AWGN–Rauschens.
Bei einem (n, 1, n)–Wiederholungscode ergibt sich dagegen für den Eingangswert des ML–Decoders y ' = x̃ ' + η ' mit folgenden Eigenschaften:
\[\tilde{x} \hspace{0.04cm}' \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i=1 }^{n} \tilde{x}_i \in \{ +n, -n \}\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fache \hspace{0.15cm}Amplitude} \hspace{0.2cm} \Rightarrow\hspace{0.2cm}n^2{\rm -fache \hspace{0.15cm}Leistung}\hspace{0.05cm},\] \[\eta\hspace{0.04cm}' \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i=1 }^{n} \eta_i\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fache \hspace{0.15cm}Varianz:\hspace{0.15cm}} \sigma^2 \rightarrow n \cdot \sigma^2\hspace{0.05cm},\] \[\rho\hspace{0.04cm}' \hspace{-0.1cm} = \hspace{-0.1cm} \frac{n^2}{n \cdot \sigma^2} = n \cdot \rho \hspace{0.2cm} \Rightarrow\hspace{0.2cm}{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{n \cdot \frac{2E_{\rm S}}{N_0}})\hspace{0.05cm}.\]
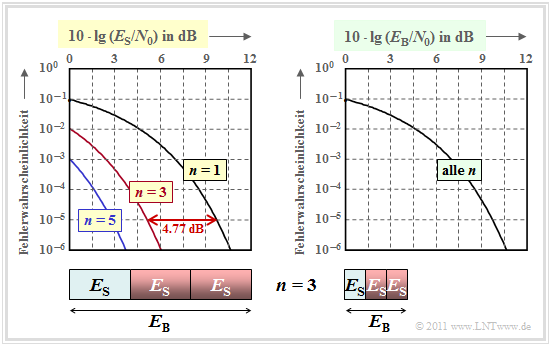
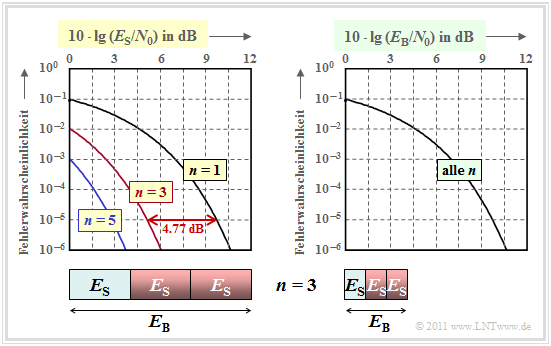
Die linke Grafik zeigt die Fehlerwahrscheinlichkeit in doppelt logarithmischer Darstellung. Als Abszisse ist 10 · lg (ES/N0) aufgetragen. Die Bildbeschreibung folgt auf der nächsten Seite.
Wiederholungscodes (3)
Es folgt nun die Interpretation der angegebenen Grafiken.
Die linke Grafik kann wie folgt interpretiert werden:
- Trägt man die Fehlerwahrscheinlichkeit über der Abszisse 10 · lg (ES/N0) auf, so ergibt sich durch n–fache Wiederholung gegenüber uncodierter Übertragung (n = 1) eine signifikante Verbesserung.
- Die Kurve für den Wiederholungsfaktor n erhält man durch Linksverschiebung um 10 · lg n (in dB) gegenüber der Vergleichskurve. Der Gewinn beträgt 4.77 dB (n = 3) bzw. ca. 7 dB (n = 5).
- Allerdings ist ein Vergleich bei konstantem ES nicht fair, da man mit einem (5, 1) Repetition Code für die Übertragung eines Informationsbits eine um den Faktor n größere Energie aufwendet:
- \[E_{\rm B} = \frac{E_{\rm S}}{R} = n \cdot E_{\rm S} \hspace{0.05cm}.\]
Aus der rechten Grafik erkennt man, dass alle Kurven genau übereinander liegen, wenn auf der Abszisse 10 · lg (EB/N0) aufgetragen wird. Daraus folgt:
Zusammenfassung der Ergebnisse für den Wiederholungscode bei AWGN
- Die Fehlerwahrscheinlichkeit ist bei fairem Vergleich unabhängig vom Wiederholungsfaktor n:
- \[{\rm Pr}(v \ne u) = {\rm Q}\left (\sqrt{\frac{2E_{\rm B}}{N_0}} \right ) \hspace{0.05cm}.\]
- Beim AWGN–Kanal ist durch einen Wiederholungscode kein Codiergewinn zu erzielen.
Hamming–Codes (1)
Richard Wesley Hamming hat 1962 eine Klasse binärer Blockcodes angegeben, die sich durch die Anzahl m = 2, 3, ... der zugesetzten Parity Bits unterscheiden. Für diese Codeklasse gilt:
- Die Codelänge ergibt sich zu n = 2m – 1. Möglich sind demzufolge beim Hamming–Code nur die Längen n = 3, n = 7, n = 15, n = 31, n = 63, n = 127, n = 255, usw.
- Ein Informationswort besteht aus k = n – m Bit. Die Coderate ist somit gleich
- \[R = \frac{k}{n} = \frac{2^m - 1 - m}{2^m - 1} \in \{1/3, \hspace{0.1cm}4/7,\hspace{0.1cm}11/15,\hspace{0.1cm}26/31,\hspace{0.1cm}57/63, \hspace{0.1cm}120/127,\hspace{0.1cm}247/255, \hspace{0.05cm} ... \hspace{0.05cm} \}\hspace{0.05cm}.\]
- Alle Hamming–Codes weisen die minimale Distanz dmin = 3 auf. Bei größerer Codelänge n erreicht man die minimale Distanz 3 schon mit weniger Redundanz, also bei größerer Coderate R.
- Aus der Angabe dmin = 3 folgt weiter, dass hier e = dmin – 1 = 2 Fehler erkannt werden können und t = (dmin – 1)/2 = 1 Fehler korrigiert werden kann.
- Der Hamming–Code (3, 1, 3) ist identisch mit dem Wiederholungscode (3, 1, 3):
- \[\mathcal{C} = \{ (0, 0, 0) \hspace{0.05cm}, (1, 1, 1) \}\hspace{0.05cm}. \]
- Bei systematischer Codierung sind die ersten k Stellen eines jeden Codewortes identisch mit dem Informationswort. Anschließend folgen bei einem Hamming–Code die m = n – k Paritätsbit:
- \[\underline{x} = ( x_1, x_2, ... \hspace{0.05cm}, x_n) = ( u_1, u_2, ... \hspace{0.05cm}, u_k, p_1, p_2, ... \hspace{0.05cm}, p_{n-k}) \hspace{0.05cm}.\]
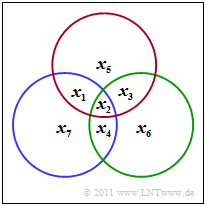
Im Folgenden betrachten wir stets den (7, 4, 3)–Hamming–Code, der durch das folgende Schaubild verdeutlicht wird. Daraus lassen sich die drei Bedingungen ableiten:
\[x_1 \oplus x_2 \oplus x_3 \oplus x_5 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},\] \[x_2 \oplus x_3 \oplus x_4 \oplus x_6 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},\] \[x_1 \oplus x_2 \oplus x_4 \oplus x_7 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm}. \]
Im Schaubild kennzeichnet der rote Kreis die erste Prüfgleichung, der grüne die zweite und der blaue die letzte. In jedem Kreis muss die Anzahl der Einsen geradzahlig sein.