Grundlegendes zu den Low–density Parity–check Codes

1. Kanalcodierung
2. Iterative Decodierverfahren
3. Grundlegendes zu den Low–density Parity–check Codes

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Einige Charakteristika der LDPC–Codes (1)

Die Low–density Parity–check Codes – kurz LDPC–Codes – wurden bereits Anfang der 1960er Jahre erfunden und gehen auf die Dissertation [Gal63] von Robert G. Gallager zurück.

Die Idee kam allerdings aufgrund der damaligen Prozessorentechnologie um einige Jahrzehnte zu früh. Schon drei Jahre nach Berrou's Erfindung der Turbocodes 1993 erkannten dann allerdings David J. C. MacKay und Radford M. Neal das riesige Potential der LDPC–Codes, wenn man diese ebenso wie die Turbocodes iterativ symbolweise decodiert. Sie erfanden die LDPC–Codes quasi neu.

Wie aus dem Namensbestandteil „Parity–check” bereits hervorgeht, handelt es sich bei diesen Codes um lineare Blockcodes entsprechend den Ausführungen in Kapitel 1. Deshalb gilt auch hier:

• Das Codewort ergibt sich aus dem Informationswort u (dargestellt mit k Binärsymbolen) und der Generatormatrix G der Dimension k×n zu x = u · G  ⇒  Codewortlänge n.
  

• Die Prüfgleichungen ergeben sich aus der Identität x · H^T ≡ 0, wobei H die Prüfmatrix bezeichnet. Diese besteht aus m Zeilen und n Spalten. Während im ersten Kapitel grundsätzlich m = n – k gegolten hat, fordern wir für die LPDC–Codes lediglich noch m ≥ n – k.
  
  

Ein gravierender Unterschied zwischen einem LDPC–Code und einem herkömmlichen Blockcode nach der Beschreibung im ersten Kapitel ist, dass die Prüfmatrix H nur spärlich mit Einsen besetzt ist.

: Die Grafik zeigt beispielhaft die Prüfmatrizen H für

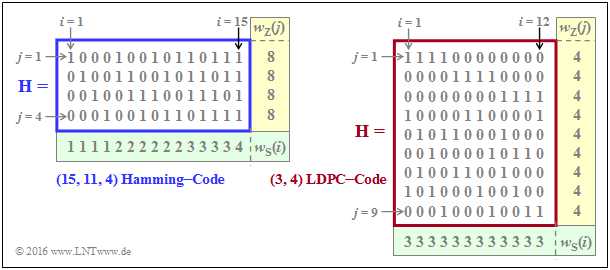
• den Hamming–Code mit Codelänge n = 15, m = 4  ⇒  k = 11 Informationsbits,
  

• den LDPC–Code aus [Liv15] der Länge n = 12 und mit m = 9 Prüfgleichungen  ⇒  k ≥ 3.
  
  

In der linken Grafik beträgt der Anteil der Einsen 32/60 ≈ 53.3%, wohingegen in der rechten Grafik der Einsen–Anteil mit 36/108 = 33.3% geringer ist. Bei den für die Praxis relevanten LDPC–Codes (großer Länge) ist der Einsen–Anteil noch deutlich niedriger.

Hinweis: Auf der nächsten Seite wird auf diese Grafik noch mehrmals Bezug genommen.

Einige Charakteristika der LDPC–Codes (2)

Wir analysieren nun die beiden Prüfmatrizen anhand der Rate und des Hamming–Gewichts.

• Die Rate des betrachteten Hamming–Codes (linke Grafik) ist R = k/n = 11/15 ≈ 0.733. Das Hamming–Gewicht einer jeden der vier Zeilen ist w_Z = 8, während die Hamming–Gewichte w_S(i) der Spalten zwischen 1 und 4 variieren. Für die Spalten–Laufvariable gilt hier: 1 ≤ i ≤ 15.

• Beim betrachteten LDPC–Code gibt es in allen Zeilen vier Einsen  ⇒  w_Z = 4 und in allen Spalten drei Einsen ⇒ w_S = 3. Die Codebezeichnung (w_Z, w_S) LDPC–Code verwendet genau diese Parameter. Beachten Sie die unterschiedliche Nomenklatur zum „(n, k, m) Hamming–Code”.

• Man spricht hier von einem regulären LDPC–Code, da alle Zeilengewichte w_Z(j) für 1 ≤ j ≤ m konstant gleich w_Z sind und auch alle Spaltengewichte (mit den Indizes 1 ≤ i ≤ n) gleich sind: w_S(i) = w_S = const. Ist diese Bedingung nicht erfüllt, so liegt ein irregulärer LDPC–Code vor.

• Für die Coderate kann man allgemein (also, wenn k nicht bekannt ist) nur eine Schranke angeben: R ≥ 1 – w_S/w_Z. Das Gleichheitszeichen gilt dann, wenn alle Zeilen von H linear unabhängig sind  ⇒  m = n – k. Dann ergibt sich die herkömmliche Gleichung: R = 1 – w_S/w_Z = 1 – m/n = k/n.

• Dagegen gilt für die Coderate eines irregulären LDPC–Codes und auch für den links skizzierten (15, 11, 4) Hammingcode:

\[R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} \hspace{0.5cm}{\rm mit}\hspace{0.5cm} {\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n}w_{\rm S}(i) \hspace{0.5cm}{\rm und}\hspace{0.5cm} {\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{ m}w_{\rm Z}(j) \hspace{0.05cm}.\]

Da beim Hamming–Code die m = n – k Prüfgleichungen linear voneinander unabhängig sind, kann das „≥”–Zeichen durch das Gleichheitszeichen ersetzt werden, was gleichzeitig R = k/n bedeutet.

Weitere Informationen zu diesem Thema finden Sie in Aufgabe A4.11 und in Aufgabe Z4.11

Zweiteilige LDPC–Graphenrepräsentation – Tanner–Graph (1)

Alle wesentlichen Merkmale eines LDPC–Codes sind in der Prüfmatrix H = (h_j,i) enthalten und lassen sich durch einen so genannten Tanner–Graphen darstellen. Es handelt sich um eine Bipartite Graph Representation, wobei die deutsche Übersetzung von „bipartite” in etwa „zweiteilig” lautet. Bevor wir beispielhafte Tanner–Graphen genauer betrachten und analysieren, müssen zuerst noch einige geeignete Beschreibungsgrößen definiert werden:

• Die n Spalten der Prüfmatrix H stehen jeweils für ein Codewortbit. Da jedes Codewortbit sowohl ein Informationsbit als auch ein Prüfbit sein kann, hat sich hierfür die neutrale Bezeichnung Varibale Node (VN) durchgesetzt. Das i–te Codewortbit wird V_i genannt und die Menge aller Variable Nodes (VNs) ist {V₁, ..., V_i, ..., V_n}.
  

• Die m Zeilen von H beschreiben jeweils eine Prüfgleichung (englisch: Parity–check Equation). Wir bezeichnen im folgenden eine solche Prüfgleichung als Check Node (CN). Die Menge aller Check Nodes (CNs) ist {C₁, ..., C_j, ..., C_m}, wobei C_j die Prüfgleichung der j–ten Zeile angibt.
  

• Im Tanner–Graphen werden die n Variable Nodes V_i als Kreise und die m Check Nodes C_j als Quadrate dargestellt. Ist das Matrixelement in Zeile j und Spalte i ⇒ h_j,i = 1, so gibt es eine Verbindungslinie (englisch: Edge) zwischen dem Variable Node V_i und dem Check Node C_j.
  
  

:

Sie sehen rechts einen beispielhaften Tannergraphen zur Verdeutlichung obiger Begriffe mit

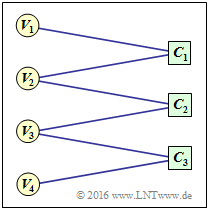
• den Variable Nodes (kurz: VNs) V₁ bis V₄, und
  

• den Check Nodes (kurz: CNs) C₁ bis C₃.
  
  

Der zugehörige Code hat allerdings keinerlei praktische Bedeutung. Man erkennt aus der Grafik:

• Die Codelänge ist n = 4 und es gibt m = 3 Prüfgleichungen. Damit hat die Prüfmatrix H die Dimension 3×4.
  

• Es gibt insgesamt sechs Verbindungslinien (englisch: Edges). Damit sind sechs der zwölf Elemente h_j,i von H Einsen.
  

• Bei jedem Check Node kommen zwei Linien an. Das bedeutet, dass die Hamming–Gewichte aller Zeilen gleich sind: w_S(j) = 2 = w_S.
  

• Von den Knoten V₁ und V₄ gibt es jeweils nur einen Übergang zu einem Check Node, von V₂ und V₃ dagegen zwei. Aus diesem Grund handelt es sich um einen irregulären Code.
  
  

Die Prüfmatrix lautet demnach:

\[{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &0 &0\\ 0 &1 &1 &0\\ 0 &0 &1 &1 \end{pmatrix}\hspace{0.05cm}.\]

Auf der nächsten Seite folgt ein praxisrelevanteres Beispiel.

Zweiteilige LDPC–Graphenrepräsentation – Tanner–Graph (2)

: In Aufgabe A4.11 wurden zwei Prüfmatrizen analysiert:

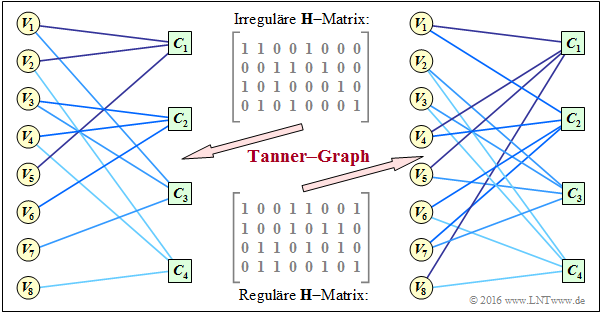
• Der Coder entsprechend der Matrix H₁ ist systematisch. Die Codeparameter sind n = 8, k = 4 und m = 4 ⇒ Rate 1/2. Der Code ist irregulär, da die Hamming–Gewichte nicht für alle Spalten gleich sind. In der folgenden Grafik ist diese „irreguläre H–Matrix” oben angegeben.
  

• Unten angegeben ist die „reguläre H–Matrix” entsprechend der Matrix H₃ in Aufgabe A4.11. Die Zeilen sind Linearkombinationen der oberen Matrix. Für diesen nicht systematischen Coder gilt mit w_S = 2 und w_Z = 4 ebenfalls:

\[R \ge 1 - \frac{w_{\rm S}}{w_{\rm Z}} = 1 - \frac{2}{4} = 1/2 \hspace{0.05cm}.\]

Die Grafik zeigt die zugehörigen Tanner–Graphen:

• Der linke Graph bezieht sich auf die irreguläre Matrix. Die acht Variable Nodes (abgekürzt VNs) V_i sind mit den vier Check Nodes (abgekürzt CNs) C_j verbunden, falls das Element in Zeile j und Spalte i  ⇒  h_j,i gleich 1 ist. Andernfalls (falls h_j,i = 0) besteht keine Verbindung.
  

• Der links dargestellte Graph ist für die iterative symbolweise Decodierung nicht sonderlich gut geeignet. Die VNs V₅, ...., V₈ sind jeweils nur mit einem CN verbunden, was für die Decodierung keinerlei Information liefert.
  

• Im rechten Tanner–Graph für den regulären Code erkennt man, dass hier von jedem VN V_i zwei Verbindungslinien (englisch: Edges) abgehen und von jedem CN C_j deren vier. Damit ist bei der Decodierung in jeder Iterationsschleife ein Informationsgewinn möglich.
  

• Man erkennt zudem, dass hier beim Übergang vom irregulären zum äquivalenten regulären Code der Einsen–Anteil zunimmt, im Beispiel von 37.5% auf 50%. Diese Aussage kann allerdings nicht verallgemeinert werden.

Iterative Decodierung von LDPC–Codes (1)

Als Beispiel für die iterative LDPC–Decodierung wird nun der sog. Message–passing Algorithm beschrieben. Wir verdeutlichen diesen anhand des rechten Tanner–Graphen auf der vorherigen Seite und damit für die dort angegebene reguläre Prüfmatrix.

Bei diesem Decodieralgorithmus erfolgt abwechselnd (oder iterativ) ein Informationsaustausch zwischen den Variable Nodes (VNs) V₁, ... , V_n und den Check Nodes (CNs) C₁, ... , C_m.

Für das betrachtete Beispiel gilt:

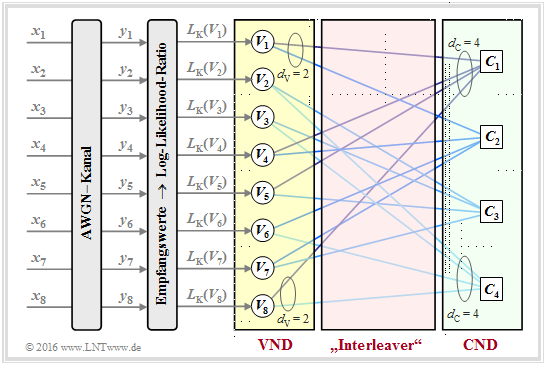
• Es gibt n = 8 VNs und m = 4 CNs. Da ein regulärer LDPC–Code vorliegt, gehen von jedem VN d_V = 2 Verbindungslinien zu einem CN und jeder CN ist mit d_C = 4 VNs verbunden.

• Der Variable Node Degree d_V ist gleich dem Hamming–Gewicht einer jeden Spalte (w_S) und für den Check Node Degree gilt: d_C = w_Z (Hamming–Gewicht einer jeden Zeile).

• In der folgenden Beschreibung verwenden wir auch die Begriffe Nachbarn eines VN  ⇒  N(V_i) sowie Nachbarn eines CN  ⇒  N(C_j), wobei wir uns hier auf implizite Definitionen beschränken:

\[N(V_1) \hspace{-0.15cm} = \hspace{-0.15cm} \{ C_1, C_2\}\hspace{0.05cm}, \hspace{0.3cm}N(V_1) = \{ C_3, C_4\}\hspace{0.05cm}, \hspace{0.05cm}.\hspace{0.05cm}.\hspace{0.05cm}.\hspace{0.15cm},\hspace{0.3cm}N(V_8) = \{ C_1, C_4\}\hspace{0.05cm},\]

\[N(C_1) \hspace{-0.15cm} = \hspace{-0.15cm} \{ V_1, V_4, V_5, V_8\}\hspace{0.05cm}, \hspace{0.05cm}.\hspace{0.05cm}.\hspace{0.05cm}.\hspace{0.15cm}\hspace{0.05cm}, \hspace{0.3cm}N(C_4) = \{ V_2, V_3, V_6, V_8\}\hspace{0.05cm}.\]

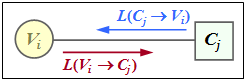
Die Skizze aus [Liv15] zeigt den Austausch von Information zwischen dem Variable Node V_i und dem Check Node C_j – ausgedrückt durch Log–Likelihood Ratios (kurz: L–Werte). Der Informationsaustausch geschieht in zwei Richtungen:

• L(V_i → C_j): Extrinsische Information aus Sicht von V_i, Apriori–Information aus Sicht von C_j.
  

• L(C_j → V_i): Extrinsische Information aus Sicht von C_j, Apriori–Information aus Sicht von V_i.
  

Iterative Decodierung von LDPC–Codes (2)

Die Beschreibung des Decodieralgorithmus wird fortgesetzt:

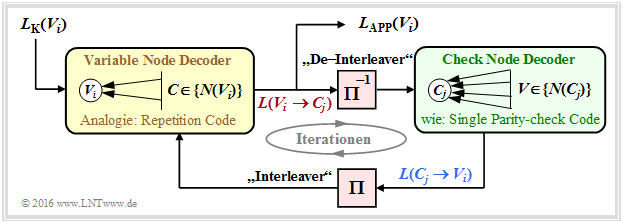
Initialisierung: Zu Beginn der Decodierung erhalten die Variable Nodes (VNs) keine Apriori–Information von den Check Nodes (CNs), und es gilt für 1 ≤ i ≤ n: L(V_i → C_j) = L_K(V_i). Wie aus der letzten Grafik ersichtlich, ergeben sich diese Kanal–L–Werte L_K(V_i) aus den Empfangswerten y_i.

Check Node Decoder: Jeder Knoten C_j repräsentiert eine Prüfgleichung. So steht C₁ für „V₁ + V₄ + V₅ + V₈ = 0”. Man erkennt den Zusammenhang zur extrinsischen Information bei der symbolweisen Decodierung des Single Parity–check Codes. In Analogie zu Kapitel 4.1 und Aufgabe A4.4 gilt somit für den extrinsischen L–Wert von C_j und gleichzeitig für die Apriori–Information bezüglich V_i:

\[L(C_j \rightarrow V_i) = 2 \cdot {\rm tanh}^{-1}\left [ \prod\limits_{V \in N(C_j)\hspace{0.05cm},\hspace{0.1cm} V \ne V_i} \hspace{-0.35cm}{\rm tanh}\left [L(V \rightarrow C_j \right ] /2) \right ] \hspace{0.05cm}.\]

Variable Node Decoder: Im Gegensatz zum Check Node Decoder (CND) besteht beim Variable Node Decoder (VND) eine Verwandtschaft zur Decodierung eines Repetition Codes, weil alle mit V_i verbundenen Check Nodes C_j demselben Bit entsprechen  ⇒  dieses Bit wird quasi d_V mal wiederholt.

In Analogie zu Kapitel 4.1 gilt für den extrinsischen L–Wert von V_i und gleichzeitig für die Apriori–Information bezüglich C_j:

\[L(V_i \rightarrow C_j) = L_{\rm K}(V_i) + \hspace{-0.55cm} \sum\limits_{C \hspace{0.05cm}\in\hspace{0.05cm} N(V_i)\hspace{0.05cm},\hspace{0.1cm} C \hspace{0.05cm}\ne\hspace{0.05cm} C_j} \hspace{-0.55cm}L(C \rightarrow V_i) \hspace{0.05cm}.\]

Das folgende Schaubild des beschriebenen Decodieralgorithmus' für LDPC–Codes zeigt Ähnlichkeiten mit der Vorgehensweise bei seriell verketteten Turbocodes. Um eine vollständige Analogie zwischen der LDPC– und der Turbodecodierung herzustellen, ist auch hier zwischen dem Variable Node Decoder (VND) und dem Check Node Decoder (CND) ein Interleaver sowie ein De–Interleaver eingezeichnet. Da es sich hierbei nicht um reale Systemkomponenten handelt, sondern nur um Analogien, haben wir diese Begriffe in Hochkommata gesetzt.