Aufgabe 1.1: Würfelspiel Mäxchen

• Zurück zum Buch

A1.1 Würfelspiel Mäxchen

Bei dem Würfelspiel „Mäxchen” wird jeweils mit zwei Würfeln geworfen. Die höhere Augenzahl der beiden Würfel wird mit $10$ multipliziert und dann die niedrigere Augenzahl dazu addiert. Beispielsweise liefert eine „2“ und eine „4“ das Spielresultat $42$ und eine „5“ und eine „6“ das Ergebnis $65$. Das kleinstmögliche Resultat eines Wurfes ist somit $31$. Weiter gelten folgende Regeln:

• Ein „Pasch” (zweimal die gleiche Augenzahl) wird im Allgemeinen höher bewertet als zwei ungleiche Würfel.
• So ist ein „Einser-Pasch” höher als $65$, aber niedriger als jeder andere Pasch.
• Eine Sonderstellung nimmt bei diesem Spiel das „Mäxchen” (eine „1” und eine „2”) ein. Diese im Bild dargestellte Kombination steht noch über dem Sechser-Pasch.

Der Spieler $X$ beginnt. Er gewinnt, wenn der Spieler $Y$ das vorgelegte Resultat nicht überbieten kann. Die weiteren vielfältigen Optionen dieses Spiels werden hier nicht berücksichtigt.

Hinweise:

• Die Aufgabe gehört zum Kapitel Einige grundlegende Definitionen der Wahrscheinlichkeitsrechnung.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Der Inhalt dieses Abschnitts ist in einem Lernvideo zusammengefasst:

Klassische Definition der Wahrscheinlichkeit

Fragebogen

1

Haben $X$ und $Y$ gleiche Gewinnchancen? Wenn Sie der Meinung sind, dass das Spiel unfair ist: Wie könnte man das Spiel fair gestalten?

	Die Spieler $X$ und $Y$ haben gleiche Chancen.
	Der Spieler $X$ ist im Vorteil.
	Der Spieler $Y$ ist im Vorteil.

2

Wieviele unterschiedliche Resultate $I$ sind bei diesem Spiel möglich?

$I \ =$

3

Wie groß ist die Wahrscheinlichkeit für einen Sechser-Pasch?

$\rm Pr[Sechser-Pasch]\ =$

4

Wie groß ist die Wahrscheinlichkeit, dass man „irgendeinen” Pasch würfelt?

$\rm Pr[irgendein \;Pasch]\ =$

5

Mit welcher Wahrscheinlichkeit würfelt ein Spieler ein „Mäxchen”?

$\rm Pr[Mäxchen]\ =$

6

Der Spieler $X$ hat eine „3” und eine „5” vorgelegt. Wie groß ist unter dieser Annahme die Gewinnchance von Spieler $Y$?

${\rm Pr}[Y\; {\rm gewinnt}]\ =$

7

Welches Spielergebnis $R_{\rm \min}$ muss der Spieler $X$ mindestens erzielen, damit er eine größere Gewinnchance als $75\%$ hat?

$R_{\rm \min}\ =$

Musterlösung

Musterlösung

1. Der Spieler X ist im Vorteil, da ihn der Spieler $Y$ überbieten muss. Das Spiel wäre dann fair, wenn es bei exakt gleichen Würfen unentschieden gewertet würde. Über einen längeren Zeitraum würden sich allerdings auch dann gleiche Gewinnchancen ergeben, wenn $X$ und $Y$ abwechselnd beginnen.

2. Es sind hier I = 21 unterschiedliche Resultate möglich. Diese sind (beim niedrigsten beginnend): 31, 32, 41, 42, 43, 51, 52, 53, 54, 61, 62, 63, 64, 65, 11, 22, 33, 44, 55, 66, 21.

3. Die 21 möglichen Resultate dieses Würfelspiels sind allerdings nicht gleichwahrscheinlich, deshalb können die Wahrscheinlichkeiten auch nicht nach der klassischen Definition (mit Ergebnis: 1/21) ermittelt werden. Macht man zumindest gedanklich eine Unterscheidung zwischen den Würfeln, zum Beispiel durch einen blauen ($B$) und einen roten ($R$) Würfel, so gibt es $6^{2} = 36$ gleichwahrscheinliche Ereignisse, unter Anderem das Ereignis $[Sechser-Pasch] = (B = 6) \cap (R = 6)$. Bei beiden Würfeln ist die Wahrscheinlichkeit für eine „6“ gleich 1/6. Da die Augenzahlen der beiden Würfel natürlich statistisch unabhängig sind, ist

$Pr[Sechser-Pasch] = Pr(B = 6 \cap R = 6) = 1/36 = 0.0278$

"Anmerkung": Aus der Namensgebung Resultat könnte man fälschlicherweise schließen, dass es sich hierbei um ein Ergebnis handelt. Entsprechend den Definitionen in Kapitel 1.1 ist das Resultat aber als ein Ereignis (Zusammenfassung von Ergebnissen) zu betrachten.

4. Diese Wahrscheinlichkeit kann mit $K = 6$ und $M = 36$ wie folgt angegeben werden:

$Pr[irgendein Pasch] = Pr(B = R) = K/M = 1/6 = 0.1667$.

5. Analog ist die Wahrscheinlichkeit für das Mäxchen mit $K = 2$ und $M = 36$ berechenbar:

$Pr[Mäxchen] = Pr(B = 1 \cap R = 2) + Pr(b = 2 \cap R = 1) = 1/18 = 0.0556$.

6. Die Wahrscheinlichkeit, dass $Y$ gewinnt, wenn $X$ das Ergebnis „53” vorgelegt hat, ist $5/9$.

Als Musterlösung dieser Teilaufgabe gibt es mit «Weiter» eine kurze Videosequenz (Dauer 1:40).

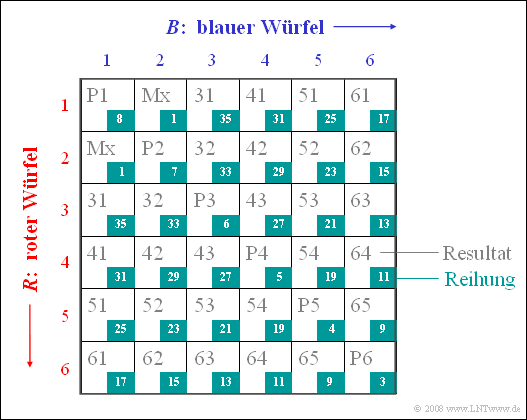
7. Zur Lösung dieser Teilaufgabe gehen wir wieder von einer zweidimensionalen Darstellung aus und reihen die Matrixelemente entsprechend ihren Wertigkeiten (siehe Bild):

Daraus ist zu ersehen, dass man mit der Vorgabe „$65$” dem Gegenspieler nur eine Gewinnchance von $8/36 = 0.222$ lässt. Damit ist seine eigene Gewinnchance etwa $77.8%$. Mit „$64$” wäre die Gewinnchance von Spieler $X$ nur ca. $72.2%$. Die richtige Lösung ist somit $R_\min = 65$.