Aufgabe 3.5Z: Antennengebiete

• Zurück zum Buch

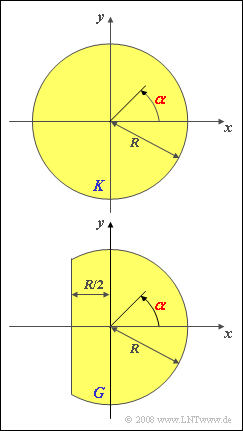
Wir betrachten zunächst - wie im oberen Bild skizziert - eine Empfangsantenne, die ein kreisförmiges Gebiet $K$ versorgt. Es wird hierbei vorausgesetzt, dass die Antenne „$K$” alle unter unterschiedlichen Winkeln $\alpha$ einfallenden Signale gleich gut detektieren kann:

• Entsprechend der Skizze bezieht sich der Winkel $\alpha$ auf die $x$–Achse.
• Der Wert $\alpha = 0$ bedeutet demnach, dass sich das Signal in Richtung der negativen $x$–Achse auf die Antenne zu bewegt.

Weiter setzen wir voraus:

• Der Wertebereich des Einfallswinkels $\alpha$ beträgt mit dieser Definition $-\pi < \alpha \le +\pi$.
• Es halten sich sehr viele Teilnehmer im Versorgungsgebiet auf, deren Positionen $(x, y)$) „statistisch” über das Gebiet $K$ verteilt sind.

Ab der Teilaufgabe (5) gehen wir von dem unten skizzierten Versorgungsgebiet $G$ aus. Wegen eines Hindernisses muss nun die $x$–Koordinate aller Teilnehmer stets größer als $-R/2$ sein. Im nun nicht mehr kreisförmigen Versorgungsgebiet $G$ seien die Teilnehmer wieder „statistisch verteilt”.

Hinweise:

• Die Aufgabe gehört zum Kapitel Gleichverteilte Zufallsgröße.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Wie lautet die WDF $f_\alpha(\alpha)$? Welcher Wert ergibt sich für $\alpha = 0$?

$\text{Gebiet }K\text{:}\hspace{0.4cm} f_\alpha(\alpha = 0) \ = $

2

Welche der beiden Aussagen ist richtig? Beachten Sie insbesondere auch den unsymmetrischen Definitionsbereich von $-\pi < \alpha \le +\pi$.

	Der Erwartungswert ist ${\rm E}[\alpha] = 0$.
	Der Erwartungswert ${\rm E}[\alpha] \ne 0$.

3

Welcher Wert ergibt sich für die Streuung der Zufallsgröße $\alpha$?

$\text{Gebiet }K\text{:}\hspace{0.4cm} \sigma_\alpha \ = $

4

Wie groß ist die Wahrscheinlichkeit, dass die Antenne einen Teilnehmer unter einem Winkel zwischen $-45^\circ$ und $+45^\circ$ ortet?

$\text{Gebiet }K\text{:}\hspace{0.4cm}{\rm Pr}(–π/4 ≤ α ≤ +π/4) \ =$

5

Nun betrachten wir das untere Versorgungsgebiet $G$. In welchem Bereich $-alpha_0 \le \alpha \le +alpha_0$ hat diese WDF $f_\alpha(\alpha)$ einen konstanten Wert?

$\text{Gebiet }G\text{:}\hspace{0.4cm}\alpha_0 \ =$ = $ \ \rm rad$

6

Welche Aussagen sind hinsichtlich $f_\alpha(\alpha) im Bereich $-|\alpha| >+alpha_0$ gültig?

	Die WDF hat „außen” den gleichen Verlauf wie „innen”.
	Die WDF ist hier $0$.
	Die WDF fällt in diesem Bereich zu den Rändern hin ab.
	Die WDF steigt in diesem Bereich zu den Rändern hin an.

7

Berechnen Sie für das Gebiet $G$ die Wahrscheinlichkeit, dass die Antenne einen Teilnehmer unter einem Winkel zwischen $\pm 45^\circ$ ortet. Interpretation.

$\text{Gebiet }G\text{:}\hspace{0.4cm} {\rm Pr}(–π/4 ≤ α ≤ +π/4) \ =$

8

Wie groß ist nun der WDF–Wert an der Stelle $\alpha = 0$?

$\text{Gebiet }G\text{:}\hspace{0.4cm} f_\alpha(\alpha\ =\ 0)$

Musterlösung

Musterlösung

1.  Es liegt eine Gleichverteilung vor und es gilt für die WDF im Bereich –π < α ≤ +π:

$$f_\alpha(\alpha)={\rm 1}/({\rm 2\cdot \pi}).$$

Bei α = 0 ergibt sich somit – wie bei allen zulässigen Werten auch – der WDF-Wert 0.159.

2.  Es gilt E[α] = 0. Es hat keinen Einfluss, dass α = +π erlaubt, aber α = –π ausgeschlossen ist.

3.  Für die Varianz gilt:

$$\sigma_{\alpha}^{\rm 2}=\int_{-\rm\pi}^{\rm\pi}\hspace{-0.1cm}\it\alpha^{\rm 2}\cdot \it f_{\alpha}(\alpha)\,\,{\rm d} \alpha=\frac{\rm 1}{\rm 2\cdot\it \pi}\cdot \frac{\alpha^{\rm 3}}{\rm 3}\Bigg|_{\rm -\pi}^{\rm\pi}=\frac{\rm 2\cdot\pi^{3}}{\rm 2\cdot\rm \pi\cdot \rm 3}=\frac{\rm \pi^2}{\rm 3} = \rm 3.29.$$

Damit ist die Streuung σ_α = 1.814.

4.  Da der vorgegebene Kreisausschnitt genau ein Viertel der gesamten Kreisfläche ausmacht, ist die gesuchte Wahrscheinlichkeit 25%.

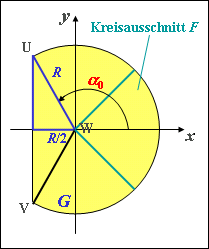
5.  Aus einfachen geometrischen Überlegungen (rechtwinkliges Dreieck, in der nebenstehenden Skizze blau markiert) erhält man die Bestimmungsgleichung für den Winkel α₀:

$$\rm cos(\pi-\it\alpha_{\rm 0}) = \frac{\it R/\rm 2}{\it R}=\frac{\rm 1}{\rm 2}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}\rm\pi-\it\alpha_{\rm 0}=\frac{\rm\pi}{\rm 3} \hspace{0.2cm}(\rm 60^{\circ}).$$

Daraus folgt α₀ = 2π/3 = 2.094 (dies entspricht 120°).

6.  Richtig ist der Lösungsvorschlag 3: Die Wahrscheinlichkeitsdichtefunktion (WDF) f_α(α) ist für einen gegebenen Winkel α direkt proportional zum Abstand A zwischen der Antenne und der Begrenzungslinie. Bei α = ±2π/3 (120°) gilt A = R, bei α = ±π (180°) dagegen A = R/2. Dazwischen wird der Abstand sukzessive kleiner. Das heißt: die WDF fällt zu den Rändern hin ab. Der Abfall erfolgt hierbei nach folgendem Verlauf:

$$\it A=\frac{\it R/\rm 2}{\rm cos(\rm \pi-\it\alpha)}.$$

7.  Die Fläche G kann aus der Summe des 240°-Sektors und des durch die Eckpunkte UVW gebildeten Dreiecks berechnet werden:

$$G=\frac{\rm 2}{\rm 3}\cdot \it R^{\rm 2}\cdot{\rm \pi} + \frac{\it R}{\rm 2}\cdot \it R\cdot \rm sin(\rm 60^{\circ}) = \it R^{\rm 2}\cdot \rm\pi\cdot (\frac{\rm 2}{\rm 3}+\frac{\rm \sqrt{3}}{\rm 4\cdot\pi}).$$

Die gesuchte Wahrscheinlichkeit ergibt sich als das Verhältnis der Flächen F und G (siehe Bild):

$$\rm Pr(\rm -\pi/4\le\it\alpha\le+\rm\pi/4)=\frac{\it F}{\it G}=\frac{1/4}{2/3+{\rm sin(60^{\circ})}/({\rm 2\pi})}=\frac{\rm 0.25}{\rm 0.805}\hspace{0.15cm}\underline{=\rm 0.311}.$$

Obwohl sich gegenüber Punkt 4. an der Fläche F nichts geändert hat, wird die Wahrscheinlichkeit nun aufgrund des kleineren Gebietes G um den Faktor 1/0.805 ≈ 1.242 größer.

8.  Da die WDF-Fläche insgesamt konstant gleich 1 ist und die WDF an den Rändern abnimmt, muss sie im Bereich |α| < 2π/3 einen größeren Wert als unter a) berechnet besitzen. Mit den Ergebnissen aus a) und g) gilt:

$$f_{\alpha}(\alpha = 0)=\frac{1/(2\pi)}{2/3+{\rm sin(\rm 60^{\circ})}/({\rm 2\pi})} = \frac{\rm 1}{{\rm 4\cdot\pi}/{\rm 3}+\rm sin(60^{\circ})}\hspace{0.15cm}\underline{\approx \rm 0.198}.$$

Wie die unter Punkt 7. berechnete Wahrscheinlichkeit nimmt auch gleichzeitig der WDF-Wert im Bereich |α| < 2π/3 um den Faktor 1.242 zu, wenn das Versorgungsgebiet kleiner wird.