Zweidimensionale Gaußsche Zufallsgrößen

Inhaltsverzeichnis

1 Wahrscheinlichkeitsdichte- und Verteilungsfunktion
2 Höhenlinien bei unkorrelierten Zufallsgrößen
3 Höhenlinien bei korrelierten Zufallsgrößen
4 Drehung des Koordinatensystems
5 Aufgaben zum Kapitel

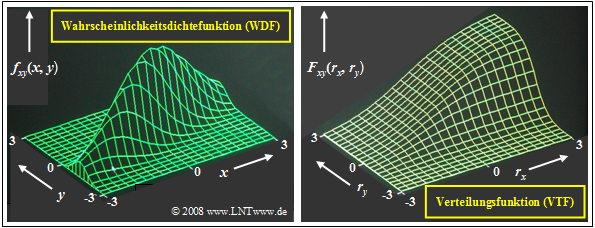
Wahrscheinlichkeitsdichte- und Verteilungsfunktion

Alle bisherigen Aussagen des Kapitels „ Zufallsgrößen mit statistischen Bindungen&rquo; 4 gelten allgemein. Für den Sonderfall Gaußscher Zufallsgrößen – der Name geht auf den Wissenschaftler Carl Friedrich Gauß zurück – können wir weiterhin vermerken:

Die Verbundwahrscheinlichkeitsdichtefunktion einer Gaußschen 2D-Zufallsgröße $(x, y)$ mit den Mittelwerten $m_x = 0$ und $m_y = 0$ sowie dem Korrelationskoeffizienten $ρ_{xy}$ lautet:

$$f_{xy}(x,y)=\frac{\rm 1}{\rm 2\it\pi \cdot \sigma_x \cdot \sigma_y \sqrt{\rm 1-\rho_{\it xy}^2}}\cdot\exp\Bigg[-\frac{\rm 1}{\rm 2 (1-\it\rho_{xy}^{\rm 2} {\rm)}}\cdot(\frac {\it x^{\rm 2}}{\sigma_x^{\rm 2}}+\frac {\it y^{\rm 2}}{\sigma_y^{\rm 2}}-\rm 2\it\rho_{xy}\cdot\frac{x \cdot y}{\sigma_x \cdot \sigma_y}\rm ) \rm \Bigg].$$

Ersetzt man in dieser Gleichung $x$ durch $(x – m_x)$ sowie $y$ durch $(y – m_y)$, so ergibt sich die allgemeinere WDF einer zweidimensionalen Gaußschen Zufallsgröße mit Mittelwert.
Die beiden Randwahrscheinlichkeitsdichtefunktionen $f_{x}(x)$ und $f_{y}(y)$ einer Gaußschen 2D-Zufallsgröße sind ebenfalls gaußförmig und weisen die Streuungen $σ_x$ bzw. $σ_y$ auf.
Bei unkorrelierten Komponenten $x$ und $y$ muss in obiger Gleichung $ρ_{xy} = 0$ eingesetzt werden, und man erhält dann das Ergebnis:

$$f_{xy}(x,y)=\frac{1}{\sqrt{2\pi}\cdot\sigma_{x}} \cdot\rm e^{-\it {x^{\rm 2}}/{\rm (}{\rm 2\it\sigma_{x}^{\rm 2}} {\rm )}} \cdot\frac{1}{\sqrt{2\pi}\cdot\sigma_{\it y}}\cdot e^{-\it {y^{\rm 2}}/{\rm (}{\rm 2\it\sigma_{y}^{\rm 2}} {\rm )}} = \it f_{x} \rm ( \it x \rm ) \cdot \it f_{y} \rm ( \it y \rm ) .$$

Resümee: Im Sonderfall einer 2D-Zufallsgröße mit Gaußscher WDF $f_{xy}(x, y)$ folgt aus der Unkorreliertheit auch direkt die statistische Unabhängigkeit: $$f_{xy}(x,y)= f_{x}(x) \cdot f_{y}(y) . $$

Bitte beachten Sie:

Bei keiner anderen WDF kann aus der Unkorreliertheit auf die statistische Unabhängigkeit geschlossen werden.
Man kann aber stets ⇒ für jede beliebige 2D–WDF $f_{xy}(x, y)$ von der statistischen Unabhängigkeit auf die Unkorreliertheit schließen, weil:
Sind zwei Zufallsgrößen $x$ und $y$ völlig voneinander (statistisch) unabhängig, so gibt es zwischen ihnen natürlich auch keine linearen Abhängigkeiten ⇒ sie sind dann auch unkorreliert.

: Die beiden Grafiken zeigen

die Wahrscheinlichkeitsdichtefunktion (links) und
Verteilungsfunktion (rechts)

einer zweidimensionalen Gaußschen Zufallsgröße $(x, y)$ mit relativ starker positiver Korrelation der Einzelkomponenten: $ρ_{xy} = 0.8$.
Wie bei den bisherigen Beispielen ist die 2D–Zufallsgröße in $x$–Richtung weiter ausgedehnt als in $y$–Richtung: $σ_x = 2 · σ_y$.

Diese Darstellungen können wie folgt interpretiert werden:

Die WDF ist vergleichbar mit einem Bergkamm, der sich von links unten nach rechts oben erstreckt.
Das Maximum liegt bei $m_x = 0$ und $m_y = 0$. Das bedeutet, dass die die 2D–Zufallsgröße mittelwertfrei ist.
Die zweidimensionale VTF als das Integral in zwei Richtungen über die WDF steigt von links unten nach rechts oben von $0$ auf $1$ kontinuierlich an.

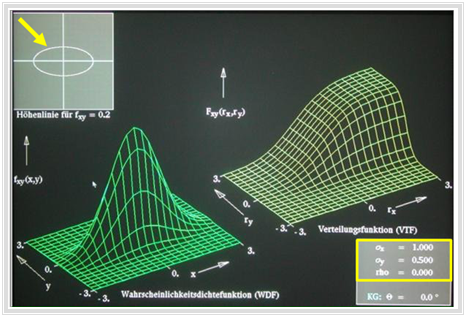
Das Modul WDF/VTF bei 2D-Gaußgrößen erlaubt die Darstellung der zweidimensionalen Funktionen für beliebige Werte von $σ_x, σ_y$ und $ρ_{xy}$.

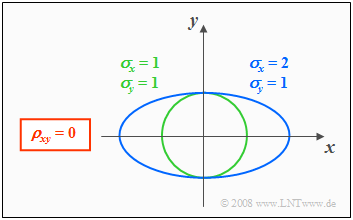
Höhenlinien bei unkorrelierten Zufallsgrößen

Aus der Bedingungsgleichung $f_{xy}(x, y) =$ const. können die Höhenlinien der WDF berechnet werden. Sind die Komponenten $x$ und $y$ unkorreliert $(ρ_{xy} = 0)$, so erhält man als Gleichung für die Höhenlinien:

Höhenlinien der 2D-WDF bei unkorrelierten Größen

$$\frac{x^{\rm 2}}{\sigma_{x}^{\rm 2}}+\frac{y^{\rm 2}}{\sigma_{y}^{\rm 2}} =\rm const.$$

Die Höhenlinien beschreiben in diesem Fall folgende Figuren:

Kreise (falls $σ_x = σ_y$, grüne Kurve), oder
Ellipsen (für $σ_x ≠ σ_y$, blaue Kurve) in Ausrichtung der beiden Achsen.

Bildschirmabzug des hier zitierten Lernvideos

Weitere Informationen zu dieser Thematik mit Signalbeispielen bietet das Lernvideo Gaußsche Zufallsgrößen ohne statistische Bindungen.

Links sehen Sie eine Momentaufnahme dieses Lernvideos.

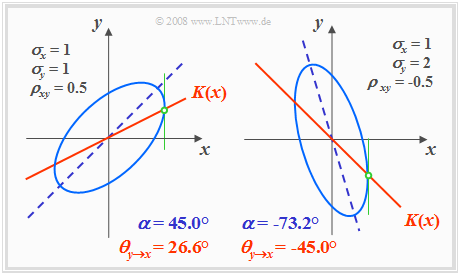
Höhenlinien bei korrelierten Zufallsgrößen

Bei korrelierten Komponenten $(ρ_{xy} ≠ 0)$ sind die Höhenlinien der WDF stets elliptisch, also auch für den Sonderfall $σ_x = σ_y$. Hier lautet die Bestimmungsgleichung der WDF-Höhenlinien:

$$f_{xy}(x, y) = {\rm const.} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \frac{x^{\rm 2} }{\sigma_{x}^{\rm 2}}+\frac{y^{\rm 2} }{\sigma_{y}^{\rm 2} }-{\rm 2}\cdot\rho_{xy}\cdot\frac{x\cdot y}{\sigma_x\cdot \sigma_y}={\rm const.}$$

Die folgende Grafik zeigt in hellerem Blau zwei Höhenlinien für unterschiedliche Parametersätze, jeweils mit $ρ_{xy} ≠ 0$.

Höhenlinien der 2D-WDF bei korrelierten Größen

Die Ellipsenhauptachse ist dunkelblau gestrichelt, und
die Korrelationsachse $K(x)$ durchgehend rot eingezeichnet.

Anhand dieser Darstellung sind folgende Aussagen möglich:

Die Ellipsenform hängt außer vom Korrelationskoeffizienten $ρ_{xy}$ auch vom Verhältnis der beiden Streuungen $σ_x$ und $σ_y$ ab.
Auch der Neigungswinkel $α$ der Ellipsenhauptachse (gestrichelte Gerade) gegenüber der $x$-Achse hängt von diesen drei Parametern ab:

$$\alpha = {1}/{2} \cdot {\rm arctan } ( 2 \cdot \rho_{xy} \cdot \frac {\sigma_x \cdot \sigma_y}{\sigma_x^2 - \sigma_y^2}).$$

Die Korrelationsgerade $y = K(x)$ einer Gaußschen 2D–Zufallsgröße liegt stets unterhalb der Ellipsenhauptachse.
$K(x)$ kann auch aus dem Schnittpunkt der Höhenlinien und ihrer vertikalen Tangenten geometrisch konstruiert werden, wie in den obigen Skizzen in grüner Farbe angedeutet ist.

Die folgenden Lernvideos beschreiben die Eigenschaften Gaußscher Zufallsgrößen: Gaußsche Zufallsgrößen ohne statistische Bindungen (Dauer 2:35), Gaußsche Zufallsgrößen mit statistischen Bindungen (Dauer 3:05).

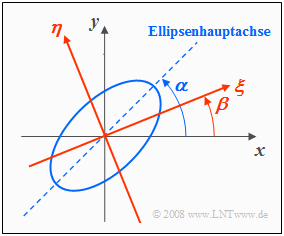
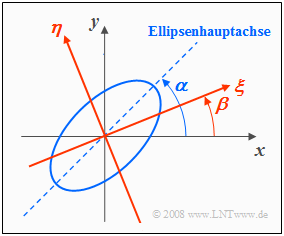
Drehung des Koordinatensystems

Bei manchen Aufgabenstellungen ist es vorteilhaft, das Koordinatensystem zu drehen, wie in der nachfolgenden Grafik angedeutet:

Das $(ξ, η)$-Koordinatensystem ist gegenüber dem ursprünglichen $(x, y)$-System um den Winkel $β$ gedreht.
Dagegen bezeichnet $α$ den Winkel zwischen der Ellipsenhauptachse und der $x$–Achse.

Zwischen den Koordinaten der beiden Bezugssysteme bestehen folgende Zusammenhänge: $$\xi = \hspace{0.4cm} \cos (\beta) \cdot x + \sin (\beta) \cdot y \hspace{0.55cm}{\rm bzw. }\hspace{0.5cm} x = \cos (\beta) \cdot \xi - \sin (\beta) \cdot \eta ,$$ $$\eta = - \sin (\beta) \cdot x + \cos (\beta) \cdot y \hspace{0.5cm}{\rm bzw. }\hspace{0.5cm} y = \sin (\beta) \cdot \xi + \cos (\beta) \cdot \eta .$$

Ist $(x, y)$ eine Gaußsche 2D-Zufallsgröße, so ist die neue Zufallsgröße $(ξ, η)$ ebenfalls gaußverteilt.

Setzt man die obigen Gleichungen in die 2D-WDF $f_{\rm xy}(x, y)$ ein und vergleicht die Koeffizienten, so erhält man folgende Bestimmungsgleichungen für $σ_x, σ_y$ und $ρ_{xy}$ bzw. für $σ_ξ, σ_η$ und $ρ_{ξη}$:

$$\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi^2} = \frac {1}{(1 - \rho_{xy}^2) } \left[ \frac {\cos^2 (\beta)}{\sigma_{x}^2 } + \frac {\sin^2 (\beta)}{\sigma_{y}^2 } - 2 \rho_{xy} \cdot \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{x} \cdot \sigma_{y}}\right ] ,$$ $$\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\eta^2} = \frac {1}{(1 - \rho_{xy}^2) } \left[ \frac {\sin^2 (\beta)}{\sigma_{x}^2 } + \frac {\cos^2 (\beta)}{\sigma_{y}^2 } + 2 \rho_{xy} \cdot \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{x} \cdot \sigma_{y}}\right ] ,$$ $$\frac {\rho_{\xi \eta}}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi\cdot \sigma_\eta}= \hspace{11cm}\\ = \frac {1}{(1 - \rho_{xy}^2) } \left[ \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{x}^2 } - \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{y}^2 } + \frac {\rho_{xy}}{\sigma_{x} \cdot \sigma_{y}} \cdot ( \cos^2( \beta) -\sin^2( \beta)) \right ] .$$

Mit diesen drei Gleichungen können die jeweils drei Parameter der beiden Koordinatensysteme direkt umgerechnet werden, was allerdings nur in Sonderfällen ohne erheblichen Rechenaufwand möglich ist. Ein solches Beispiel folgt nachfolgend.

Wir betrachten eine Gaußsche 2D-WDF mit $σ_x = σ_y =$ 1 und $ρ_{xy} =$ 0.5. In diesem Fall beträgt der Winkel $α$ der Ellipsenhauptachse 45°.

Dreht man das Koordinatensystem ebenfalls um $(β =)$ 45°, so ergibt sich wegen $σ_x = σ_y$ und wegen $\sin(β) = \cos(β) = {\rm0.5^{½}}$ für den neuen Korrelationskoeffizienten $ρ_{ξη} =$ 0, was einsichtig ist.
Die beiden Streuungen – bezogen auf das neue Koordinatensystem – ergeben sich dann entsprechend den beiden ersten oberen Gleichungen zu $σ_ξ = {\rm 1.5^{½}}$ und $σ_η = {\rm 0.5^{½}}$.

Dem obigen Bild ist allerdings nicht $β = α$ zugrundegelegt, sondern $β = α/2$. Dann lautet das Gleichungssystem mit $σ_x = σ_y =$ 1, $ρ_{xy} =$ 0.5, $α =$ 45°, $\sin(β) · \cos(β) = \sin(2β)/2 = \sin(α)/2$ und $\cos^2(β) – \sin^2(β) = \cos(2β)= \cos(α)$:

$${\rm (I)}\hspace{0.4cm}\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi^2} = \frac {4}{3} \left[ 1 - \frac {1}{2}\cdot {\sin (\alpha) }\right ] = 0.862 ,$$ $${\rm (II)}\hspace{0.28cm}\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\eta^2} = \frac {4}{3} \left[ 1 + \frac {1}{2}\cdot {\sin (\alpha) }\right ] = 1.805 ,\hspace{0.28cm}\frac {\rm (I)}{\rm (II)}: \frac {\sigma_\eta}{\sigma_\xi} = \sqrt{\frac{0.862}{1.805}}= 0.691,$$ $${\rm (III)}\hspace{0.14cm}\frac {\rho_{\xi \eta}}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi\cdot \sigma_\eta}= \frac {\rho_{\xi \eta}}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi^2 \cdot 0.691}=\frac {2}{3}\cdot \cos( \alpha) = 0.471.$$

Dividiert man nun die Gleichung (III) durch die Gleichung (I), so erhält man: $$ \frac {\rho_{\xi \eta}}{0.691}=\frac {0.471}{0.862}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}{\rho_{\xi \eta}}= 0.378.$$

Die beiden weiteren Parameter ergeben sich zu $σ_ξ$ ≈ 1 und $σ_η$ ≈ 0.7.

Aufgaben zum Kapitel

Aufgabe 4.1: Dreieckiges (x, y)-Gebiet

Aufgabe 4.1Z: Verabredung zum Frühstück

Aufgabe 4.1: Wieder Dreieckgebiet

Aufgabe 4.2Z: Korrelation zwischen $x$ und $e^x$

Aufgabe 4.3: Algebraische und Modulo-Summe

Aufgabe 4.3Z: Diracförmige 2D-WDF