Stochastische Systemtheorie
Dieses Kapitel beschreibt den Einfluss eines Filters auf die Autokorrelationsfunktion (AKF) und das Leistungsdichtespektrum (LDS) stochastischer Signalen. Weitere Informationen zum Thema „Filterung stochastischer Signale” sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
- Kapitel 10: Filterung stochastischer Signale (Programm fil)
- Kapitel 11: Optimale Filter (Programm ofi)
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms, und
- der Praktikumsanleitung - Teil B ⇒ Link verweist auf die PDF-Version mit Kapitel 10: Seite 229-248 und Kapitel 11: Seite 249-270.
Der erste Abschnitt „Stochastische Systemtheorie” dieses Kapitels ist wie folgt gegliedert:
Inhaltsverzeichnis
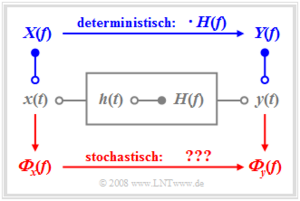
Problemstellung
Wir betrachten wie im Buch Lineare zeitinvariante Systeme die rechts skizzierte Anordnung, wobei das System
- sowohl durch die Impulsantwort $h(t)$
- als auch durch seinen Frequenzgang $H(f)$
eindeutig beschrieben ist. Der Zusammenhang zwischen diesen Beschreibungsgrößen im Zeit- und Frequenzbereich ist durch die Fouriertransformation gegeben.
Legt man an den Eingang das Signal $x(t)$ an und bezeichnet das Ausgangssignal mit $y(t)$, so liefert die klassische Systemtheorie folgende Aussagen:
- Das Ausgangssignal $y(t)$ ergibt sich aus der Faltung zwischen dem Eingangssignal $x(t)$ und der Impulsantwort $h(t)$:
- $$y(t) = x(t) \ast h(t) = \int_{-\infty}^{+\infty} x(\tau)\cdot h ( t - \tau) \,\,{\rm d}\tau.$$
- Diese Gleichung gilt für deterministische und stochastische Signale gleichermaßen.
- Bei deterministischen Signalen geht man meist den Umweg über die Spektralfunktionen. Das Eingangsspektrum $X(f)$ ist die Fouriertransformierte von $x(t)$. Die Multiplikation mit dem Frequenzgang $H(f)$ führt zum Spektrum $Y(f)$. Das Signal $y(t)$ lässt sich daraus durch die Fourierrücktransformation gewinnen.
- Bei stochastischen Signalen versagt diese Vorgehensweise, da dann die Zeitfunktionen $x(t)$ und $y(t)$ nicht für alle Zeiten von $–∞$ bis $+∞$ vorhersagbar sind und somit die dazugehörigen Amplitudenspektren $X(f)$ und $Y(f)$ gar nicht existieren. In diesem Fall muss auf die im letzten Kapitel definierten Leistungsdichtespektren übergegangen werden.
Amplituden- und Leistungsdichtespektrum
Wir betrachten nun einen ergodischen Zufallsprozess $\{x(t)\}$, dessen Autokorrelationsfunktion $φ_x(τ)$ als bekannt vorausgesetzt wird. Das Leistungsdichtespektrum ${\it Φ}_x(f)$ ist dann über die Fouriertransformation ebenfalls eindeutig bestimmt und es gelten die folgenden Aussagen:
- Das Leistungsdichtespektrum ${\it Φ}_x(f)$ kann – ebenso wie die Autokorrelationsfunktion $φ_x(τ)$ – für jede einzelne Musterfunktion des stationären und ergodischen Zufallsprozesses $\{x(t)\}$ angegeben werden, auch wenn der spezifische Verlauf von $x(t)$ explizit nicht bekannt ist.
- Das Amplitudenspektrum $X(f)$ ist dagegen undefiniert, da bei Kenntnis der Spektralfunktion $X(f)$ auch die gesamte Zeitfunktion $x(t)$ von $–∞$ bis $+∞$ über die Fourierrücktransformation bekannt sein müsste, was bei einem stochastischen Signal eindeutig nicht der Fall sein kann.
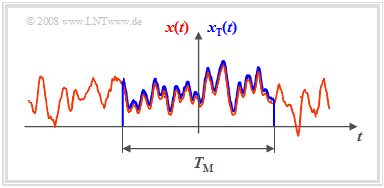
- Ist entsprechend der nachfolgenden Skizze ein Zeitausschnitt der endlichen Zeitdauer $T_{\rm M}$ bekannt, so kann für diesen natürlich wieder die Fouriertransformation angewandt werden.
Satz: Zwischen dem Leistungsdichtespektrum ${\it Φ}_x(f)$ des unendlich ausgedehnten Zufallssignals $x(t)$ und dem Amplitudenspektrum $X_{\rm T}(f)$ des begrenzten Zeitausschnittes $x_{\rm T}(t)$ besteht dabei der folgende Zusammenhang:
- $${{\it \Phi}_x(f)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot |X_{\rm T}(f)|^2.$$
Beweis: Vorne wurde die
Autokorrelationsfunktion eines ergodischen Prozesses mit der Musterfunktion $x(t)$ wie folgt angegeben:
- $${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot x(t + \tau)\hspace{0.1cm} \rm d \it t.$$
Es ist hier zulässig, die zeitlich unbegrenzte Funktion $x(t)$ durch die auf den Zeitbereich $–T_{\rm M}/2$ bis $+T_{\rm M}/2$ begrenzte Funktion $x_{\rm T}(t)$ zu ersetzen. $x_{\rm T}(t)$ korrespondiert mit der Spektralfunktion $X_{\rm T}(f)$, und man erhält durch Anwendung des ersten Fourierintegrals und des Verschiebungssatzes:
- $${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot \int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x_{\rm T}(t)\cdot \int^{+\infty}_{-\infty}X_{\rm T}(f)\cdot {\rm e}^{{\rm j}2 \pi f ( t + \tau) } \hspace{0.1cm} \rm d \it f \hspace{0.1cm} \rm d \it t.$$
Nach Aufspalten des Exponenten und Vertauschen von Zeit- und Frequenzintegral ergibt sich:
- $${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot \int^{+\infty}_{-\infty}X_{\rm T}(f)\cdot \left[ \int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x_{\rm T}(t)\cdot {\rm e}^{{\rm j}2 \pi f t } \hspace{0.1cm} \rm d \it t \right] \cdot {\rm e}^{{\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f.$$
Das innere Integral beschreibt das konjugiert–komplexe Spektrum $X_{\rm T}^{\star}(f)$. Daraus folgt weiter:
- $${{\it \varphi}_x(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot \int^{+\infty}_{-\infty}|X_{\rm T}(f)|^2 \cdot {\rm e}^{{\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f.$$
Ein Vergleich mit dem bei Ergodizität stets gültigen Theorem von Wiener und Chintchine,
- $${{\it \varphi}_x(\tau)} = \int^{+\infty}_{-\infty}{\it \Phi}_x(f) \cdot {\rm e}^{{\rm j}2 \pi f \tau} \hspace{0.1cm} \rm d \it f ,$$
zeigt die Gültigkeit der oben genanntenBeziehung:
- $${{\it \Phi}_x(f)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}}\cdot |X_{\rm T}(f)|^2.$$
Leistungsdichtespektrum des Filterausgangssignals
Kombiniert man die in den beiden letzten Abschnitten gemachten Aussagen, so kommt man zu folgendem wichtigen Ergebnis:
Satz: Das Leistungsdichtespektrum (LDS) am Ausgang eines linearen zeitinvarianten Systems mit dem Frequenzgang $H(f)$ ergibt sich als das Produkt aus dem Eingangs–LDS ${\it Φ}_x(f)$ und der Leistungsübertragungsfunktion $|H(f)|^2$.
- $${{\it \Phi}_y(f)} = {{\it \Phi}_x(f)} \cdot |H(f)|^2.$$
Beweis: Ausgegangen wird von den drei bereits vorher hergeleiteten Beziehungen:
- $${{\it \Phi}_x(f)} =\hspace{-0.1cm} \lim_{T_{\rm M}\to\infty}\hspace{0.01cm} \frac{1}{ T_{\rm M}}\hspace{-0.05cm}\cdot\hspace{-0.05cm} |X_{\rm T}(f)|^2, \hspace{0.15cm} {{\it \Phi}_y(f)} =\hspace{-0.1cm} \lim_{T_{\rm M}\to\infty}\hspace{0.01cm} \frac{1}{ T_{\rm M}}\hspace{-0.05cm}\cdot\hspace{-0.05cm} |Y_{\rm T}(f)|^2, \hspace{0.15cm} Y_{\rm T}(f) = X_{\rm T}(f) \hspace{-0.05cm}\cdot\hspace{-0.05cm} H(f).$$
Setzt man diese Gleichungen ineinander ein, so erhält man die obige Gleichung.
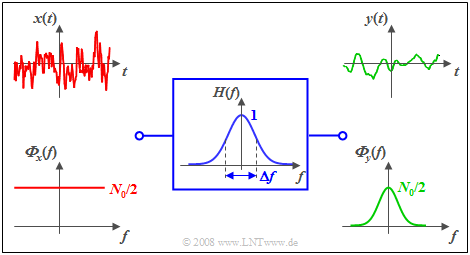
Das folgende Beispiel verdeutlicht den Zusammenhang bei Weißem Rauschen.
Beispiel: Am Eingang eines Gauß-Tiefpasses mit dem Frequenzgang $$H(f) = {\rm e}^{- \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta f)^2}$$ liegt weißes Rauschen $x(t)$ mit der (zweiseitigen) Rauschleistungsdichte ${{\it \Phi}_x(f)} =N_0/2$ an. Dann gilt für das LDS des Ausgangssignals: $${{\it \Phi}_y(f)} = \frac {N_0}{2} \cdot {\rm e}^{- 2 \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta f)^2}.$$ Die Grafik zeigt die Signale und Leistungsdichtespektren am Ein- und Ausgang des Filters. Anmerkungen:
- Das Eingangssignal $x(t)$ kann – streng genommen – gar nicht gezeichnet werden, da es eine unendlich große Leistung besitzt ⇒ Integral über ${\it Φ}_x(f)$ von $-\infty$ bis $+\infty$.
- Das Ausgangssignal $y(t)$ ist niederfrequenter als $x(t)$ und besitzt eine endliche Leistung entsprechend dem Integral über ${\it Φ}_y(f)$.
Autokorrelationsfunktion des Filterausgangssignals
Das berechnete Leistungsdichtespektrum (LDS) kann auch wie folgt geschrieben werden:
- $${{\it \Phi}_y(f)} = {{\it \Phi}_x(f)} \cdot H(f) \cdot H^{\star}(f)$$
Satz: Für die zugehörige Autokorrelationsfunktion (AKF) erhält man dann entsprechend den Gesetzen der Fouriertransformation und durch Anwendung des Faltungssatzes:
- $${{\it \varphi}_y(\tau)} = {{\it \varphi}_x(\tau)} \ast h(\tau)\ast h(- \tau).$$
Beim Übergang vom Spektral– in den Zeitbereich ist zu beachten:
- Einzusetzen sind jeweils die Fourierrücktransformierten, nämlich
- $${{\it \varphi}_y(\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{{\it \Phi}_y(f)}, \hspace{0.2cm}{{\it \varphi}_x(\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\!\bullet\,{{\it \Phi}_x(f)}, \hspace{0.2cm}{h(\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{H(f)}, \hspace{0.2cm}{h(-\tau)} \circ\hspace{0.05cm}\!\!\!-\!\!\!-\!\!\!-\!\!\!\bullet\,{H^{\star}(f)}$$
- Zudem wird aus jeder Multiplikation eine Faltungsoperation.
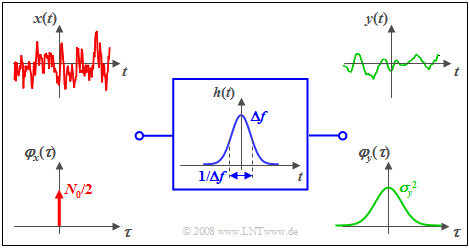
Beispiel: Wir betrachten nochmals das gleiche Beispiel wie im letzten Abschnitt, aber diesmal im Zeitbereich:
- weißes Rauschen ${{\it \Phi}_x(f)} =N_0/2$,
- gaußförmiges Filter:
- $$H(f) = {\rm e}^{- \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(f/\Delta f)^2}\hspace{0.1cm}\Rightarrow \hspace{0.1cm} h(t) = \Delta f \cdot {\rm e}^{- \pi \hspace{0.03cm}\cdot \hspace{0.03cm}(\Delta f \hspace{0.03cm}\cdot \hspace{0.03cm}t)^2}.$$
Man erkennt aus dieser Darstellung:
- Die AKF des Eingangssignals ist nun eine Diracfunktion mit dem Gewicht $N_0/2$.
- Durch zweimalige Faltung mit der (hier ebenfalls gaußförmigen) Impulsantwort $h(t)$ bzw. $h(–t)$ erhält man die AKF $φ_y(τ)$ des Ausgangssignals. Diese ist wiederum gaußförmig.
- Der AKF–Wert bei $τ = 0$ ist identisch mit der Fläche des Leistungsdichtespektrums ${\it Φ}_y(f)$ und kennzeichnet die Signalleistung (Varianz) $σ_y^2$.
- Dagegen ergibt die Fläche unter $φ_y(τ)$ den LDS-Wert ${\it Φ}_y(f = \rm 0)$, also $N_0/2$.
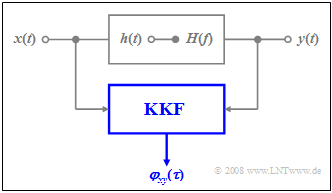
Kreuzkorrelationsfunktion zwischen Eingangs- und Ausgangssignal
Wir betrachten wieder ein Filter mit der Impulsantwort $h(t)$ sowie die stochastischen Signale $x(t)$ und $y(t)$ an seinem Eingang bzw. seinem Ausgang.
Dann gilt für die Kreuzkorrelationsfunktion (KKF) zwischen dem Eingangs– und dem Ausgangssignal:
- $${{\it \varphi}_{xy}(\tau)} = h(\tau)\ast {{\it \varphi}_x(\tau)} .$$
Hierbei gelten folgende Bezeichnungen:
- $h(τ)$ ist die Impulsantwort des Filters (mit der Zeitvariablen $τ$ anstelle von $t$),
- $φ_x(τ)$ kennzeichnet die AKF am Filtereingang.
Beweis: Allgemein gilt für die Kreuzkorrelationsfunktion zwischen zwei Signalen $x(t)$ und $y(t)$:
- $${{\it \varphi}_{xy}(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm}\frac{1}{ T_{\rm M}}\cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot y(t + \tau)\hspace{0.1cm} \rm d \it t.$$
Mit der allgemeingültigen Beziehung $y(t) = h(t) \ast x(t)$ und der formalen Integrationsvariablen $θ$ lässt sich hierfür auch schreiben:
- $${{\it \varphi}_{xy}(\tau)} = \lim_{T_{\rm M}\to\infty}\hspace{0.2cm}\frac{1}{ T_{\rm M}}\cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot \int^{+\infty}_{-\infty} h(\theta) \cdot x(t + \tau - \theta)\hspace{0.1cm}{\rm d}\theta\hspace{0.1cm}{\rm d} \it t.$$
Durch Vertauschen der beiden Integrale und Hereinziehen der Grenzwertbildung erhält man:
- $${{\it \varphi}_{xy}(\tau)} = \int^{+\infty}_{-\infty} h(\theta) \cdot \left[ \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{ T_{\rm M}} \cdot\int^{+T_{\rm M}/2}_{-T_{\rm M}/2}x(t)\cdot x(t + \tau - \theta)\hspace{0.1cm} \hspace{0.1cm} {\rm d} t \right]{\rm d}\theta.$$
Der Ausdruck in den eckigen Klammern ergibt den AKF-Wert am Eingang zum Zeitpunkt $τ – θ$:
- $${{\it \varphi}_{xy}(\tau)} = \int^{+\infty}_{-\infty}h(\theta) \cdot \varphi_x(\tau - \theta)\hspace{0.1cm}\hspace{0.1cm} {\rm d}\theta = h(\tau)\ast {{\it \varphi}_x(\tau)} .$$
Das verbleibende Integral beschreibt aber die Faltungsoperation in ausführlicher Schreibweise.
Im Frequenzbereich lautet die entsprechende Gleichung:
$${{\it \Phi}_{xy}(f)} = H(f)\cdot{{\it \Phi}_x(f)} .$$
Die beiden Gleichungen zeigen, dass der Filterfrequenzgang $H(f)$ aus einer Messung mit stochastischer Anregung vollständig – also sowohl der Betrag als auch die Phase – berechnet werden kann, wenn folgende Beschreibungsgrößen ermittelt werden:
- die statistischen Kenngrößen am Eingang, entweder die AKF $φ_x(τ)$ oder das LDS ${\it Φ}_x(f)$,
- sowie die Kreuzkorrelationsfunktion $φ_{xy}(τ)$ bzw. deren Fouriertransformierte ${\it Φ}_{xy}(f)$.
Aufgaben zum Kapitel
Aufgabe 5.1: Gaußsche AKF und Gaußtiefpass
Aufgabe 5.1Z: $\cos^2$-Rauschbegrenzung
Aufgabe 5.2: Frequenzgangbestimmung