Aufgabe 4.8: Numerische Auswertung der AWGN-Kanalkapazität

Für die Kanalkapazität C des AWGN–Kanals als obere Schranke für die Coderate R bei Digitalsignalübertragung gibt es zwei verschiedene Gleichungen :

Kanalkapazität C in Abhängigkeit von E_S/N₀: $$C( E_{\rm S}/{N_0}) = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot E_{\rm S}}{N_0}) .$$ Hierbei sind folgende Abkürzungen verwendet:

E_S: die Energie pro Symbol des Digitalsignals,
N₀: die AWGN–Rauschleistungsdichte.

Kanalkapazität C in Abhängigkeit von E_B/N₀: $$C( E_{\rm B}/{N_0}) = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) .$$

Berücksichtigt ist der Zusammenhang E_S = R · E_B, wobei R die Coderate der bestmöglichen Kanalcodierung angibt. Eine fehlerfreie Übertragung (unter Berücksichtigung dieses optimalen Codes) ist für das gegebene E_B/N₀ möglich, so lange R ≤ C gilt ⇒ Kanalcodierungstheorem von Shannon.'

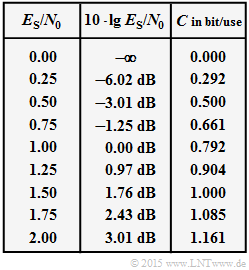
Durch die Tabelle vorgegeben ist der Kurvenverlauf C(E_S/N₀). Im Mittelpunkt dieser Aufgabe steht die numerische Auswertung der zweiten Gleichung. Hinweis

Die Aufgabe gehört zum Themengebiet von Kapitel 4.3.

Fragebogen

Musterlösung

1. 2. 3. 4. 5. 6. 7.

	Falsch
	Richtig