Aufgabe 5.6: Filterdimensionierung

• Zurück zum Buch

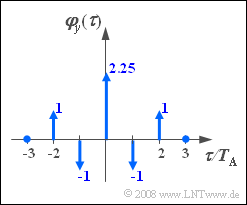
Eine zeitdiskrete Zufallsgröße $\left\langle {y_\nu } \right\rangle$mit der skizzierten AKF soll mit Hilfe eines digitalen Filters erzeugt werden. Alle AKF-Werte $\varphi_y(k \cdot T_{\rm A})$ mit Index $|k| \gt 2$ seien $0$.

Die zeitdiskreten Gaußschen Eingangswerte $x_\nu$ seien jeweils gekennzeichnet durch

• den Mittelwert $m_x = 0$,
• die Streuung $\sigma_x = 1$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Erzeugung vorgegebener AKF-Eigenschaften.
• Bezug genommen wird auch auf das Kapitel Autokorrelationsfunktion.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche der nachfolgenden Aussagen sind zutreffend?

	Es eignet sich ein rekursives Filter erster Ordnung.
	Es eignet sich ein nichtrekursives Filter erster Ordnung.
	Es eignet sich ein nichtrekursives Filter zweiter Ordnung.
	Die Ausgangswerte yν sind dreieckverteilt.
	Die Ausgangswerte yν sind mittelwertfrei (my = 0).

2

Geben Sie die Gleichungen zur Bestimmung der Koeffizienten a₀, a₁, a₂ an. Ersetzen Sie die drei Variablen durch u = a₁² und w = (a₀ + a₂)². Bestimmen Sie u und w. Hinweis: Es gibt nur eine sinnvolle Lösung.

$u$ =

$2$ =

3

Bestimmen Sie die Filterkoeffizienten a₀, a₁ und a₂. Geben Sie die folgenden Quotienten ein:

$a_1/a_0$ = -

$a_2/a_0$ =

4

Wieviele verschiedene Parametersätze (I) führen zur gewünschten AKF?

$I$ =

Musterlösung

Musterlösung

1.  Ein rekursives Filter würde stets eine unendlich weit ausgedehnte Impulsantwort h(t) und damit auch eine unendlich ausgedehnte AKF bewirken. Deshalb ist hier eine nichtrekursive Filterstruktur zu wählen. Die angegebene AKF erfordert die Ordnung M = 2.

Da die Eingangswerte gaußverteilt und mittelwertfrei sind, gilt dies auch für die Ausgangswerte. Bei der Filterung stochastischer Signale gilt stets: „Gauß bleibt Gauß und Nicht-Gauß wird nie (exakt) Gauß”. Richtig sind somit die Lösungsvorschläge 3 und 5.

2.  Das Gleichungssystem lautet:

$$k = 2:\quad a_0 \cdot a_2 = 1$$

$$k = 1:\quad a_0 \cdot a_1 + a_1 \cdot a_2 = - 1\quad \Rightarrow \quad \sqrt {u \cdot w} = - 1\quad \Rightarrow \quad u \cdot w = 1$$

$$k = 0:\quad a_0 ^2 + a_1 ^2 + a_2 ^2 = 2.25\quad \;\;\, \Rightarrow \quad u + w = 2.25 + 2a_0 \cdot a_2 = 4.25.$$

Das Gleichungssystem bezüglich u und w hat zwei Lösungen:

u = 4, w = 0.25: Wegen der Bedingung a₂ = 1/a₀ (siehe erste obere Gleichung) haben a₀ und a₂ gleiches Vorzeichen und es ist mindestens einer der beiden Koeffizienten 1 oder größer. Somit ist die Bedingung a₀ + a₂ = w^1/2 = 0.5 nicht zu erfüllen.

Die richtige Lösung lautet deshalb u = 0.25 und w = 4.

3.  Das Ergebnis von (b) bedeutet, dass a₁ = ± (0.25)^1/2 = ± 0.5 ist. Der positive Wert führt zu

$$0.5 \cdot \left( {a_0 + a_2 } \right) = - 1\quad \Rightarrow \quad a_0 + a_2 = - 2,$$

$$a_0 \cdot a_2 = 1.$$

Daraus folgt a₀ = a₂ = –1. Mit a₁ = 0.5 erhält man als Ergebnis:

$$a_1/a_0 \hspace{0.15 cm}\underline{= -0.5}, \hspace{0.5 cm} a_2/a_0 \hspace{0.15 cm}\underline{= 1}.$$

Die Lösung <nobr>a₁ = –0.5</nobr> führt zu a₀ = a₂ = 1 und damit zu den gleichen Quotienten.

4.  Allgemein hat dieses Problem I = 4 äquivalente Lösungen (Spiegelung/Verschiebung sowie jeweils die Multiplikation mit –1). Da hier die Impulsantwort symmetrisch ist, gibt es nur I = 2 Lösungen:

$$a_0 = +1\quad a_1 = - 0.5\quad a_2 = +1, $$

$$a_0 = - 1\quad a_1 = +0.5\quad a_2 = - 1. $$