Aufgabe 2.3: Zur LZ78-Komprimierung
Aus LNTwww
Version vom 21. April 2017, 13:30 Uhr von Guenter (Diskussion | Beiträge)
- Im Gegensatz zur Entropiecodierung nach Huffman oder nach Shannon, bei der man die Quellenstatistik (möglichst genau) kennen muss, sind solche Einschränkungen bei den von Abraham Lempel und Jacob Ziv entwickelten Komprimierungsverfahren nicht gegeben. Man spricht von universeller Quellencodierung.
- Wir betrachten in dieser Aufgabe die 1978 erstmals veröffentlichte Variante LZ78 Codiert werden soll der String BARBARA–BAR.
- LZ78 arbeitet mit einem globalen Wörterbuch, das zu Beginn nur mit einem leeren Zeichen (ε) unter dem Index I = 0 gefüllt ist. Dadurch unterscheidet sich LZ78 von seinem Vorgänger LZ77 (lokales Wörterbuch) und auch von seinem Nachfolger LZW (Wörterbuch ist mit den möglichen Zeichen vorbelegt).
- Wird ein Zeichen oder ein Wortfragment (mehrere Zeichen) des Eingabestrings im Wörterbuch gefunden, so wird der Index I0 dieses Eintrags zusammen mit dem nächsten Eingangszeichen Z ausgegeben. In jedem Schritt i lautet also die Ausgabe: (I0, Z).
- Anschließend wird der neue String unter dem nächsten freien Index Ineu ins Wörterbuch eingetragen. Betrachtet man das Wörterbuch als ein Feld W[I] mit I ≥ 0, bei dem ein jedes Element eine Zeichenkette beliebiger Länge enthält, so gilt mit der Character–Variablen Z:
- $$W (I_{\rm neu}) = W(I_0) + Z \hspace{0.05cm}. $$
- Zur Verdeutlichung ein einfaches Beispiel:
- Zu einem gegebenen Zeitpunkt ist das Wörterbuch bis zum Index Iakt = 20 gefüllt.
- Zur Codierung steht Handy an. Im Wörterbuch findet man unter dem Index I = 11 den Eintrag Ha und unter dem Index I = 16 den Eintrag Han.
- Somit lautet die aktuelle Coderausgabe (I0, Z) = (16, d) und ins Wörterbuch wird als neue Phrase eingetragen: W(21) = Hand.
- Nun liegt der String y zur Codierung an. Findet man hierfür keinen passenden Eintrag, so wird <nobr>(0, y)</nobr> ausgegeben und W(22) = ε + y = y neu ins Wörterbuch eingetragen.
- Für die Teilaufgabe 6) können Sie von folgenden Voraussetzungen ausgehen:
- Die Dezimalzahl I (Index) wird durch 3 Bit binär dargestellt.
- Das Zeichen Z ∈ {A, B, R, –} wird mit jeweils 2 Bit binärcodiert.
- Hinweis: Die Aufgabe bezieht sich auf das Kapitel 2.2. Ähnliche Aufgaben zu anderen LZ–Methoden finden Sie unter folgenden Links:
- Aufgabe Z2.3: LZ77-Codierung von BARBARA–BAR,
- Aufgabe A2.4: LZW–(De–)Codierung einer binären Eingangsfolge.
Fragebogen
Musterlösung
- 1. Zutreffend für den LZ78–Algorithmus ist Aussage 1. Die Vorbelegung gemäß Aussage 2 gilt dagegen für den LZW–Algorithmus, der 1983 gemeinsam mit Terry Welch veröffentlicht wurde.
- 2. ε bezeichnet das leere Zeichen. Da ε + B = B ergibt, sind die Aussagen 1 und 2 richtig. Dagegen würde die Aussage 3 wieder für die LZW–Komprimierung zutreffen.
- 3. Beide Aussagen treffen zu.
- 4. Im Wörterbuch wird unter dem Index I = 1 das Zeichen B gefunden und das nächste Zeichen A der Eingangsfolge wird angehängt: (1, A). Richtig sind somit die Aussagen 2 und 4. Die Aussage 3 kann schon deshalb nicht stimmen, da Z nur ein Zeichen sein kann und keine Zeichenfolge.
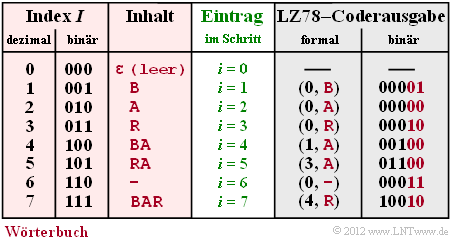
- 5. Der gesamte Codiervorgang ist in einer Tabelle zusammengefasst:
- Man erkennt:
- Zu jedem Zeitpunkt i wird die bearbeitete Zeichenfolge in das Wörterbuch eingetragen.
- Zum Zeitpunkt i = 7 ist der Codiervorgang abgeschlossen.
- 6. Stellt man alle Indizes mit 3 Bit dar und die vier Zeichen (Character) mit je 2 Bit, so kommt man zu folgenden Ergebnissen:
- ohne Codierung: N = 11 · 2 = 22 Bit,
- mit LZ78–Codierung: N = 7 · (3 + 2) = 35 Bit.
- Daran erkennt man:
- Eine jede LZ–Komprimierung macht erst bei einer größeren Datei Sinn, auch dann, wenn man glaubt, dass ein Text wie BARBARA–BAR dem LZ78–Algorithmus entgegenkommt.
- Mit variabler Bitanzahl für den Index entsprechend der Theorieseite 5 und Aufgabe A2.4 ergibt sich für dieses LZ78-Beispiel
- $$N = 1 \cdot 3 + 2 \cdot 4 + 4 \cdot 5 = 31 \,{\rm Bit}\hspace{0.05cm}.$$