Aufgabe 4.7Z: Signalformen bei ASK, BPSK und DPSK
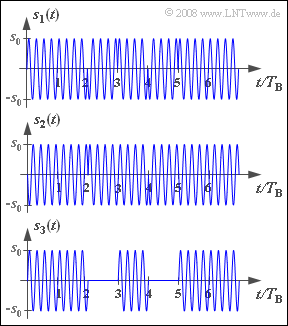
Die Abbildung zeigt jeweils ausgehend vom gleichen Quellensignal q(t) die Sendesignale bei
Amplitude Shift Keying (ASK)
Binary Phase Shift Keying (BPSK)
Differential Phase Shift Keying (DPSK)
Die Beschreibung dieser digitalen Modulationsverfahren finden Sie über die angegebenen Links im Theorieteil zu Kapitel 4.2.
Die Sendesignale sind hier allgemein mit $s_1(t)$, $s_2(t)$ und $s_3(t)$ bezeichnet. Die Zuordnung zu den vorgegebenen Modulationsverfahren soll in der Versuchsdurchführung von Ihnen vorgenommen werden.
Außerdem soll für alle Signale die jeweilige mittlere Energie pro Bit ($E_B$) in Watt (W) angegeben werden, wobei folgende Annahmen getroffen werden können:
- Die (maximale) Hüllkurve aller trägerfrequenzmodulierten Signale ist $s_0 = 2 V$.
- Die Bitrate des redundanzfreien Quellensignals beträgt $R_B = 1 Mbit/s$.
- Die Modulatoren arbeiten mit einem Arbeitswiderstand von R = 50 Ω.
Beispielsweise würde bei (bipolarer) Basisbandübertragung mit $T_B = 1/R_B$ gelten:
$$ E_{\rm B} = \frac {s_0^2 \cdot T_{\rm B} }{R} = \frac {(2\,{\rm V})^2 \cdot 10^{-6} \,{\rm s}}{50 \,{\rm V/A}}= 8 \cdot 10^{-8} \,{\rm Ws}= 0.08 \,\,{\rm \mu Ws}.$$ Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.2.
Fragebogen
Musterlösung
2. Gegenüber der bipolaren Basisbandübertragung sind bei der ASK folgende Änderungen zu erkennen:
- Die Energie wird wegen der Multiplikation mit dem Sinussignal halbiert.
- Da $q(t)$ als redundanzfrei vorausgesetzt wird, gilt in der Hälfte der Zeit $s_3(t) = 0$, wodurch die Energie nochmals halbiert wird.
Damit ergibt sich: $$E_{\rm B} = \frac {s_0^2 \cdot T_{\rm B} }{4 \cdot R} = \frac {(2\,{\rm V})^2 \cdot 10^{-6} \,{\rm s}}{4 \cdot 50 \,{\rm V/A}}= 2 \cdot 10^{-8} \,{\rm Ws}\hspace{0.15cm}\underline {= 0.02 \,\,{\rm \mu Ws}}.$$
3. Typisch für die BPSK sind Phasensprünge. Da stets das gleiche Quellensignal vorausgesetzt wurde, treten diese Phasensprünge genau dann auf, wenn im ASK–Signal $s_3(t)$ ein Symbolwechsel zu erkennen ist. Richtig ist somit der erste Lösungsvorschlag $s_1(t)$.
4. Von der unter b) genannten Veränderung gegenüber der Basisbandübertragung ist bei BPSK nur die erste zutreffend. Damit gilt:
$$E_{\rm B} = \frac {s_0^2 \cdot T_{\rm B} }{2 \cdot R} \hspace{0.15cm}\underline {= 0.04 \,\,{\rm \mu Ws}}.$$
5. Wie bereits zu vermuten ist, lautet die richtige Antwort $s_2(t)$ ⇒ Lösungsvorschlag 2. Der DPSK–Modulator arbeitet wie folgt, wobei m0 = – 1 vorausgesetzt wird: $$ m_0 = -1, \hspace{0.1cm}a_1 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_1 = -1,$$ $$m_1 = -1, \hspace{0.1cm}a_2 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_2 = -1,$$ $$m_2 = -1, \hspace{0.1cm}a_3 = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_3 = +1,$$ $$m_3 = +1, \hspace{0.1cm}a_4 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_4 = +1,$$ $$m_4 = +1, \hspace{0.1cm}a_5 = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_5 = -1,$$ $$m_5 = -1, \hspace{0.1cm}a_6 = +1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}m_6 = -1, \,\,{\rm usw.}$$
6. Ein Vergleich der beiden Signale $s_1(t)$ und $s_2(t)$ zeigt, dass sich hinsichtlich der Signalenergie nichts ändert: $E_B = 0.04 μWs$ ⇒ Die DPSK weist die genau gleiche Signalenergie auf wie die BPSK.