Signale, Basisfunktionen und Vektorräume

1. Digitalsignalübertragung
2. Verallgemeinerte Beschreibung digitaler Modulationsverfahren
3. Signale, Basisfunktionen und Vektorräume

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

# ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #

Das Hauptkapitel 4 liefert eine abstrahierte Beschreibung der Digitalsignalübertragung, die auf Basisfunktionen und Signalraumkonstellationen aufbaut. Dadurch ist es möglich, sehr unterschiedliche Konfigurationen – zum Beispiel Bandpass–Systeme und solche für das Basisband – in einheitlicher Form zu behandeln. Der jeweils optimale Empfänger besitzt in allen Fällen die gleiche Struktur.

Im Einzelnen werden behandelt:

• die Bedeutung von Basisfunktionen und deren Auffinden nach dem Gram–Schmidt–Verfahren,
• die Struktur des optimalen Empfängers für die Basisbandübertragung,
• das Theorem der Irrelevanz und dessen Bedeutung für die Herleitung optimaler Detektoren,
• der optimale Empfänger für den AWGN–Kanal und Implementierungsaspekte,
• die Systembeschreibung durch komplexes bzw. N–dimensionales Gaußsches Rauschen,
• die Fehlerwahrscheinlichkeitsberechnung und –approximation bei sonst idealen Bedingungen,
• die Anwendung der Signalraumbeschreibung auf Trägerfrequenzsysteme,
• ie unterschiedlichen Ergebnisse für OOK, M–ASK, M–PSK, M–QAM und M–FSK,
• die unterschiedlichen Ergebnisse für kohärente bzw. nichtkohärente Demodulation.

Nahezu alle Ergebnisse dieses Kapitels wurden bereits in früheren Abschnitten hergeleitet. Grundlegend neu ist jedoch die Herangehensweise:

• Im LNTwww–Buch „Modulationsverfahren” sowie in den ersten drei Kapiteln dieses Buches wurden bereits bei den Herleitungen die spezifischen Systemeigenschaften berücksichtigt – zum Beispiel, ob die Übertragung des Digitalsignals im Basisband erfolgt oder ob eine digitale Amplituden–, Frequenz– oder Phasenmodulation vorliegt.
  
• Hier sollen nun die Systeme dahingehend abstrahiert werden, dass sie einheitlich behandelt werden können. Der jeweils optimale Empfänger besitzt in allen Fällen die gleiche Struktur, und die Fehlerwahrscheinlichkeit lässt sich auch für nichtgaußverteiltes Rauschen angeben.
  
  

Anzumerken ist, dass sich durch diese eher globale Vorgehensweise gewisse Systemunzulänglichkeiten nur sehr ungenau erfassen lassen, wie zum Beispiel

• der Einfluss eines nichtoptimalen Empfangsfilters auf die Fehlerwahrscheinlichkeit,
  
• ein falscher Schwellenwert (Schwellendrift) oder
  
• Phasenjitter (Schwankungen der Abtastzeitpunkte).
  
  

Insbesondere bei Vorhandensein von Impulsinterferenzen sollte also weiterhin entsprechend dem Hauptkapitel 3 vorgegangen werden.

Die Beschreibung basiert auf dem Skript [KöZ08] von Ralf Kötter und Georg Zeitler, das sich stark an das Lehrbuch [WJ65] anlehnt. Gerhard Kramer, Lehrstuhlinhaber des LNT seit 2010, behandelt in seiner Vorlesung [Kra10] die gleiche Thematik mit sehr ähnlicher Nomenklatur.

Um unseren eigenen Studenten an der TU München das Lesen nicht unnötig zu erschweren, halten wir uns weitestgehend an diese Nomenklatur, auch wenn diese von anderen LNTwww–Kapiteln abweicht.

Zur Nomenklatur im vierten Kapitel

Gegenüber den anderen Kapiteln in „LNTwww„ ergeben sich hier folgende Nomenklaturunterschiede:

• Die zu übertragende Nachricht ist ein ganzzahliger Wert $m \in \{m_i\}$ mit $i = 0$, ... , $M-1$, wobei $M$ den Symbolumfang angibt. Wenn es die Beschreibung vereinfacht, wird $i = 1$, ... , $M$  induziert.
  

• Das Ergebnis des Entscheidungsprozesses beim Empfänger ist ebenfalls ein Integerwert mit dem gleichen Symbolalphabet wie beim Sender. Man bezeichnet dieses Ergebnis auch als den Schätzwert:

$$\hat{m} \in \{m_i \}, \hspace{0.2cm} i = 0, 1, \text{...}\hspace{0.05cm} , M-1\hspace{0.2cm} ({\rm bzw.}\,\,i = 1, 2, \text{...}\hspace{0.05cm}, M) \hspace{0.05cm}.$$

• Die Symbolfehlerwahrscheinlichkeit $\rm Pr(Symbolfehler)$ oder auch $p_{\rm S}$ wird in diesem Hauptkapitel meist wie folgt bezeichnet:

$${\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) = 1 - {\rm Pr} ({\cal C}), \hspace{0.4cm}\text{Komplementärereignis:}\hspace{0.2cm} {\rm Pr} ({\cal C}) = {\rm Pr} ( \hat{m} = m) \hspace{0.05cm}.$$

• Bei einer Wahrscheinlichkeitsdichtefunktion (WDF) wird nun entsprechend $p_r(\rho)$ zwischen der Zufallsgröße   ⇒   $r$ und der Realisierung   ⇒   $\rho$ unterschieden. Bisher wurde für eine WDF die Bezeichnung $f_r(r)$ verwendet.
  

• Mit der Schreibweise $p_r(\rho)$ geben $r$ und $\rho$ Skalare an. Sind dagegen Zufallsgröße und Realisierung Vektoren (geeigneter Länge), so wird dies durch Fettschrift ausgedrückt:     $p_{ \boldsymbol{ r}}(\boldsymbol{\rho})$ mit den Vektoren $ \boldsymbol{ r}$ und $\boldsymbol{\rho}$.

• Um Verwechslungen mit Energiewerten zu vermeiden, heißt nun der Schwellenwert $G$ anstelle von $E$ und wird in diesem Kapitel vorwiegend als Entscheidungsgrenze bezeichnet.

• Ausgehend von den beiden reellen und energiebegrenzten Zeitfunktionen $x(t)$ und $y(t)$ erhält man für das innere Produkt:

$$<\hspace{-0.1cm}x(t), \hspace{0.05cm}y(t) \hspace{-0.1cm}> \hspace{0.15cm}= \int_{-\infty}^{+\infty}x(t) \cdot y(t)\,d \it t \hspace{0.05cm}.$$

• Daraus ergibt sich die Euklidische Norm oder „2–Norm” (oder kurz „Norm”):

$$||x(t) || = \sqrt{<\hspace{-0.1cm}x(t), \hspace{0.05cm}x(t) \hspace{-0.1cm}>} \hspace{0.05cm}.$$

Gegenüber dem Skript [KöZ08] unterscheidet sich die Bezeichnungsweise hier wie folgt:

• Die Wahrscheinlichkeit des Ereignisses $E$ ist hier ${\rm Pr}(E)$ anstelle von $P(E)$. Diese Nomenklaturänderung wurde auch deshalb vorgenommen, da Wahrscheinlichkeiten und Leistungen in manchen Gleichungen gemeinsam vorkommen.
  
• Bandpass–Signale werden weiterhin mit Index „BP” gekennzeichnet und nicht wie in [KöZ08] mit einer Tilde. Das entsprechende Tiefpass–Signal ist (meist) mit dem Index „TP” versehen.
  

Orthonormale Basisfunktionen (1)

Wir gehen in diesem Kapitel von einem Satz {s_i(t)} möglicher Sendesignale aus, die den möglichen Nachrichten m_i eineindeutig zugeordnet werden können. Mit i = 1, ... , M gilt:

\[m \in \{m_i \}, \hspace{0.2cm} s(t) \in \{s_i(t) \}\hspace{-0.1cm}: m = m_i \hspace{0.1cm} \Leftrightarrow \hspace{0.1cm} s(t) = s_i(t) \hspace{0.05cm}.\]

Weiter setzen wir für das Folgende voraus, dass die M Signale s_i(t) energiebegrenzt sind, was meist gleichzeitig bedeutet, dass sie nur von endlicher Dauer sind.

: Eine jede Menge {s₁(t), ... , s_M(t)} energiebegrenzter Signale lässt sich in N ≤ M; orthonormale Basisfunktionen φ₁(t), ... , φ_N(t) entwickeln, wobei gilt:

\[s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , \hspace{0.3cm}i = 1,\hspace{0.05cm} ...\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} ... \hspace{0.1cm}, N \hspace{0.05cm}.\]

Jeweils zwei Basisfunktionen φ_j(t) und φ_k(t) müssen orthonormal zueinander sein, das heißt, es muss gelten (δ_jk nennt man das Kronecker–Symbol):

\[<\hspace{-0.1cm}\varphi_j(t), \hspace{0.05cm}\varphi_k(t) \hspace{-0.1cm}> = \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\,d \it t = {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.1cm}j = k \\ {\rm falls}\hspace{0.1cm} j \ne k \\ \end{array} \hspace{0.05cm}.\]

Der Parameter N gibt dabei an, wieviele Basisfunktionen φ_j(t) benötigt werden, um die M möglichen Sendesignale darzustellen. Mit anderen Worten: N ist die Dimension des Vektorraums, der von den M Signalen aufgespannt wird. Dabei gilt:

• Ist N = M, so sind alle Sendesignale zueinander orthogonal. Sie sind nicht notwendigerweise orthonormal, das heißt, die Energien E_i = 〈s_i(t),  s_i(t)〉 können durchaus ungleich 1 sein.
  
• N < M ergibt sich, wenn mindestens ein Signal s_i(t) als Linearkombination von Basisfunktionen φ_j(t) dargestellt werden kann, die sich aus anderen Signalen s_j(t) ≠ s_i(t) ergeben haben.
  

Orthonormale Basisfunktionen (2)

: Wir betrachten M = 3 energiebegrenzte Signale gemäß der Grafik. Man erkennt sofort, dass

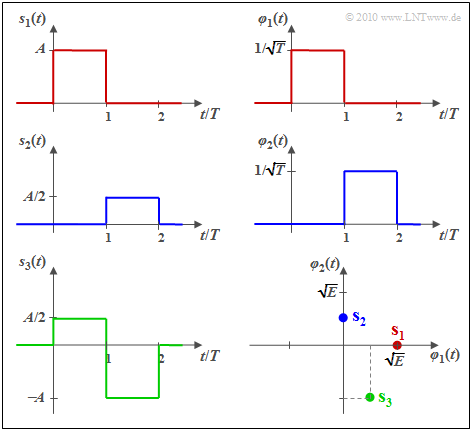
• s₁(t) und s₂(t) zueinander orthogonal sind,
  

• die Energie E₁ = A² · T = E ist und E₂ = E/4 gilt,
  

• φ₁(t) und φ₂(t) jeweils formgleich mit s₁(t) bzw. s₂(t) sind und beide die Energie 1 besitzen:

\[\varphi_1(t) \hspace{-0.15cm} = \hspace{-0.15cm}\frac{s_1(t)}{\sqrt{E_1}} = \frac{s_1(t)}{\sqrt{A^2 \cdot T}} = \frac{1}{\sqrt{ T}} \cdot \frac{s_1(t)}{A}\hspace{0.95cm}\Rightarrow \hspace{0.1cm}s_1(t) = s_{11} \cdot \varphi_1(t)\hspace{0.05cm},\hspace{0.1cm}s_{11} = \sqrt{E}\hspace{0.05cm},\]

\[\varphi_2(t) \hspace{-0.15cm} = \hspace{-0.15cm}\frac{s_2(t)}{\sqrt{E_2}} = \frac{s_2(t)}{\sqrt{(A/2)^2 \cdot T}} = \frac{1}{\sqrt{ T}} \cdot \frac{s_2(t)}{A/2}\hspace{0.05cm}\hspace{0.1cm}\Rightarrow \hspace{0.1cm}s_2(t) = s_{21} \cdot \varphi_2(t)\hspace{0.05cm},\hspace{0.1cm}s_{21} = \frac{\sqrt{E}}{2}\hspace{0.05cm}.\]

• s₃(t) durch die Basisfunktionen φ₁(t) und φ₂(t) ausgedrückt werden kann:

\[s_3(t) \hspace{-0.1cm} = \hspace{-0.1cm}s_{31} \cdot \varphi_1(t) + s_{32} \cdot \varphi_2(t)\hspace{0.05cm},\]

\[s_{31} \hspace{-0.1cm} = \hspace{-0.1cm} {A}/{2} \cdot \sqrt {T}= {\sqrt{E}}/{2}\hspace{0.05cm}, \hspace{0.2cm}s_{32} = - A \cdot \sqrt {T} = -\sqrt{E} \hspace{0.05cm}.\]

Im rechten unteren Bild sind die Signale in einer 2D–Darstellung mit den Basisfunktionen φ₁(t) und φ₂(t) als Achsen dargestellt, wobei E = A² · T gilt und der Zusammenhang zu den anderen Grafiken durch die Farbgebung zu erkennen ist. Die vektoriellen Repräsentanten der Signale s₁(t), s₂(t) und s₃(t) in diesem zweidimensionellen Vektorraum lassen sich daraus wie folgt ablesen:

\[\mathbf{s}_1 = (\sqrt{ E}, \hspace{0.1cm}0), \hspace{0.2cm} \mathbf{s}_2 = (0, \hspace{0.1cm}\sqrt{ E}/2), \hspace{0.2cm} \mathbf{s}_3 = (\sqrt{ E}/2,\hspace{0.1cm}-\sqrt{ E} ) \hspace{0.05cm}.\]

Das Verfahren nach Gram-Schmidt (1)

Im Beispiel auf der letzten Seite war die Angabe der beiden orthonormalen Basisfunktionen φ₁(t) und φ₂(t) sehr einfach, da diese formgleich mit s₁(t) und s₂(t) waren. Das Gram–Schmidt–Verfahren findet die Basisfunktionen φ₁(t), ... , φ_N(t) für beliebig vorgebbare Signale s₁(t), ... , s_M(t), und zwar wie folgt:

• Die erste Basisfunktion φ₁(t) ist formgleich mit s₁(t). Es gilt:

\[\varphi_1(t) = \frac{s_1(t)}{\sqrt{E_1}} = \frac{s_1(t)}{|| s_1(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_1(t) || = 1, \hspace{0.2cm}s_{11} =|| s_1(t)||,\hspace{0.2cm}s_{1j} = 0 \hspace{0.2cm}{\rm f{\rm \ddot{u}r }}\hspace{0.2cm} j \ge 2 \hspace{0.05cm}.\]

• Es wird nun angenommen, dass aus den Signalen s₁(t), ... , s_k–1(t) bereits die Basisfunktionen φ₁(t), ... , φ_n–1(t) berechnet wurden (n ≤ k). Dann berechnen wir mittels s_k(t) die Hilfsfunktion

\[\theta_k(t) = s_k(t) - \sum\limits_{j = 1}^{n-1}s_{kj} \cdot \varphi_j(t) \hspace{0.4cm}{\rm mit}\hspace{0.4cm} s_{kj} = \hspace{0.1cm} < \hspace{-0.1cm} s_k(t), \hspace{0.05cm}\varphi_j(t) \hspace{-0.1cm} >, \hspace{0.2cm} j = 1, ... \hspace{0.1cm}, n-1\hspace{0.05cm}.\]

• Ist θ_k(t) ≡ 0  ⇒  ||θ_k(t)|| = 0, so liefert s_k(t) keine neue Basisfunktion. Vielmehr lässt sich dann s_k(t) durch die n–1 bereits vorher gefundenen Basisfunktionen φ₁(t), ... , φ_n–1(t) ausdrücken:

\[s_k(t) = \sum\limits_{j = 1}^{n-1}s_{kj}\cdot \varphi_j(t) \hspace{0.05cm}.\]

• Eine neue Basisfunktion (nämlich die n–te) ergibt sich, falls ||θ_k(t)|| ≠ 0 ist:

\[\varphi_n(t) = \frac{\theta_k(t)}{|| \theta_k(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_n(t) || = 1\hspace{0.05cm}.\]

Diese Prozedur kann fortgesetzt werden, bis alle M Signale berücksichtigt wurden. Danach hat man alle N ≤ M orthonormalen Basisfunktionen φ_j(t) gefunden. Der Sonderfall N = M ergibt sich nur dann, wenn alle M Signale linear voneinander unabhängig sind.

Auf der nächsten Seite wird das Gram–Schmidt–Verfahren an einem einfachen Beispiel verdeutlicht. Wir verweisen auch auf das folgende Interaktionsmodul:

Gram–Schmidt–Verfahren

Das Verfahren nach Gram-Schmidt (2)

: Wir betrachten die M = 4 energiebegrenzten Signale s₁(t), ... , s₄(t) entsprechend der Grafik. Zur Vereinfachung der Berechnungen ist hier sowohl die Amplitude als auch die Zeit normiert. Man erkennt:

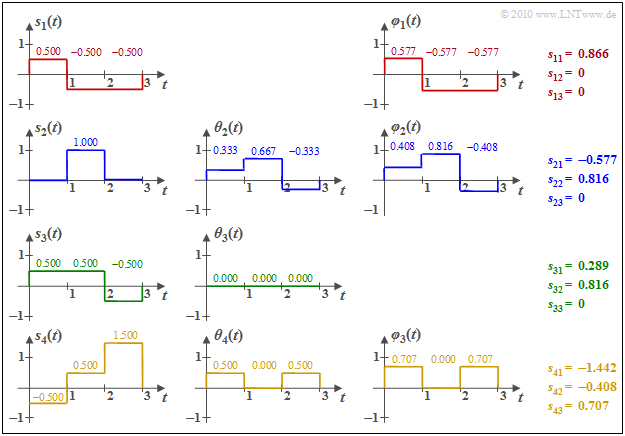
• Die Basisfunktion φ₁(t) ist formgleich mit s₁(t). Wegen E₁ = ||s₁(t)||² = 3 · 0.5² = 0.75 ergibt sich s₁₁ = ||s₁(t)|| = 0.866. φ₁(t) selbst besitzt abschnittsweise die Werte ±0.5/0.866 = ±0.577.

• Zur Berechnung der Hilfsfunktion θ₂(t) berechnen wir

\[s_{21} \hspace{-0.1cm} = \hspace{-0.1cm}\hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.05cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0 \cdot (+0.577) + 1 \cdot (-0.577)+ 0 \cdot (-0.577)= -0.577\]

\[ \hspace{-0.1cm}\Rightarrow \hspace{-0.1cm} \hspace{0.3cm}\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t) = (0.333, 0.667, -0.333)\]

\[ \hspace{-0.1cm}\Rightarrow \hspace{-0.1cm} \hspace{0.3cm}|| \theta_2(t) ||^2 = (1/3)^2 + (2/3)^2 + (-1/3)^2 = 0.667\]

\[ \hspace{-0.1cm}\Rightarrow \hspace{-0.1cm} \hspace{0.3cm} s_{22} = \sqrt{0.667} = 0.816,\hspace{0.2cm} \varphi_2(t) = \theta_2(t)/s_{22} = (0.408, 0.816, -0.408)\hspace{0.05cm}. \]

• Die inneren Produkte zwischen s₃(t) mit φ₁(t) bzw. φ₂(t) liefern folgende Ergebnisse:

\[s_{31} \hspace{0.1cm} = \hspace{0.1cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0.5 \cdot (+0.577) + 0.5 \cdot (-0.577)- 0.5 \cdot (-0.577)= 0.289\]

\[s_{32} \hspace{0.1cm} = \hspace{0.1cm} < \hspace{-0.1cm} s_3(t), \hspace{0.07cm}\varphi_2(t) \hspace{-0.1cm} > \hspace{0.1cm} = 0.5 \cdot (+0.408) + 0.5 \cdot (+0.816)- 0.5 \cdot (-0.408)= 0.816\]

\[ \hspace{0.1cm}\Rightarrow \hspace{-0.1cm} \hspace{0.3cm}\theta_3(t) = s_3(t) - 0.289 \cdot \varphi_1(t)- 0.816 \cdot \varphi_2(t) = 0\hspace{0.05cm}.\]

Das bedeutet: Die grüne Funktion s₃(t) liefert keine neue Basisfunktion φ₃(t), im Gegensatz zur Funktion s₄(t). Die numerischen Ergebnisse hierfür können der Grafik entnommen werden.

Basisfunktionen komplexer Zeitsignale

In der Nachrichtentechnik hat man es oft mit komplexen Zeitfunktionen zu tun,

• nicht etwa, weil es komplexe Signale in der Realität gibt, sondern
  

• weil die Beschreibung eines BP–Signals im äquivalenten TP–Bereich zu komplexen Signalen führt.
  
  

Die Bestimmung der N ≤ M komplexwertigen Basisfunktionen ξ_k(t) aus den M komplexen Signalen s_i(t) kann ebenfalls mit dem Gram–Schmidt–Verfahren erfolgen, doch ist nun zu berücksichtigen, dass das innere Produkt zweier komplexer Signale x(t) und y(t) wie folgt zu berechnen ist:

\[< \hspace{-0.1cm}x(t), \hspace{0.1cm}y(t)\hspace{-0.1cm} > \hspace{0.1cm} = \int_{-\infty}^{+\infty}x(t) \cdot y^{\star}(t)\,d \it t \hspace{0.05cm}.\]

Die entsprechenden Gleichungen lauten nun mit  i = 1, ... , M  und  k = 1, ... , N:

\[s_i(t) = \sum\limits_{k = 1}^{N}s_{ik} \cdot \xi_k(t),\hspace{0.2cm}s_i(t) \in {\cal C},\hspace{0.2cm}s_{ik} \in {\cal C} ,\hspace{0.2cm}\xi_k(t) \in {\cal C} \hspace{0.05cm},\]

\[< \hspace{-0.1cm}\xi_k(t),\hspace{0.1cm} \xi_j(t)\hspace{-0.1cm} > \hspace{0.1cm} = \int_{-\infty}^{+\infty}\xi_k(t) \cdot \xi_j^{\star}(t)\,d \it t = {\rm \delta}_{ik} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c}{\rm falls}\hspace{0.15cm} k = j \\ {\rm falls}\hspace{0.15cm} k \ne j \\ \end{array}\hspace{0.05cm}.\]

Natürlich lässt sich jede komplexe Größe auch durch zwei reelle Größen – nämlich durch den Realteil und den Imaginärteil – ausdrücken. Somit erhält man hier folgende Gleichungen:

\[s_{i}(t) \hspace{-0.1cm} = \hspace{-0.1cm} s_{{\rm I}i}(t) + {\rm j} \cdot s_{{\rm Q}i}(t), \hspace{0.2cm} s_{{\rm I}i}(t) = {\rm Re} [s_{i}(t)], \hspace{0.2cm} s_{{\rm Q}i}(t) = {\rm Im} [s_{i}(t)],\]

\[\xi_{k}(t) \hspace{-0.1cm} = \hspace{-0.1cm} \varphi_k(t) + {\rm j} \cdot \psi_k(t), \hspace{0.2cm} \varphi_k(t) = {\rm Re} [\xi_{k}(t)], \hspace{0.2cm} \psi_k(t) = {\rm Im} [\xi_{k}(t)],\]

\[\hspace{0.35cm} s_{ik} \hspace{-0.1cm} = \hspace{-0.1cm} s_{{\rm I}ik} + {\rm j} \cdot s_{{\rm Q}ik}, \hspace{0.2cm} s_{{\rm I}ik} = {\rm Re} [s_{ik}], \hspace{0.2cm} s_{{\rm Q}ik} = {\rm Im} [s_{ik}],\]

\[ \hspace{0.35cm} s_{{\rm I}ik} \hspace{-0.1cm} = \hspace{-0.1cm}{\rm Re}[\hspace{0.1cm} < \hspace{-0.1cm} s_i(t), \hspace{0.15cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm}], \hspace{0.2cm}s_{{\rm Q}ik} = {\rm Re}[\hspace{0.1cm} < \hspace{-0.1cm} s_i(t), \hspace{0.15cm}{\rm j} \cdot \psi_k(t) \hspace{-0.1cm} > \hspace{0.1cm}] \hspace{0.05cm}. \]

Die Nomenklatur ergibt sich aus der Hauptanwendung für komplexe Basisfunktionen, nämlich der Quadratur–Amplitudenmodulation (QAM). Der Index „I” steht für Inphasekomponente und gibt den Realteil an, während die Quadraturkomponente (Imaginärteil) mit dem Index „Q” gekennzeichnet ist.

Um Verwechslungen mit der imaginären Einheit zu vermeiden, sind hier die komplexen Basisfunktionen ξ_k(t) mit „k” induziert und nicht mit „j”.

Dimension der Basisfunktionen (1)

Bei der Basisbandübertragung sind die möglichen Sendesignale (Betrachtung nur einer Symboldauer) \[s_i(t) = a_i \cdot g_s(t), \hspace{0.2cm} i = 0, ...\hspace{0.05cm} , M-1,\]

wobei g_s(t) den Sendegrundimpuls angibt und die a_i in Kapitel 1 und Kapitel 2 als die möglichen Amplitudenkoeffizienten bezeichnet wurden. Anzumerken ist, dass im bisherigen Kapitel 4.1 für die Laufvariable i die Werte 1 bis M vorausgesetzt wurden und nicht wie hier 0 bis M – 1.

Nach der Beschreibung dieses Kapitels handelt es sich unabhängig von der Stufenzahl M um ein eindimensionales Modulationsverfahren (N = 1), wobei bei der Basisbandübertragung

• die Basisfunktion φ₁(t) gleich dem energienormierten Sendegrundimpuls g_s(t) ist:

\[\varphi_1(t) ={g_s(t)}/{\sqrt{E_{gs}}} \hspace{0.3cm}{\rm mit}\hspace{0.3cm} E_{gs} = \int_{-\infty}^{+\infty}g_s^2(t)\,d \it t \hspace{0.05cm},\]

• die dimensionslosen Amplitudenkoeffizienten a_i in die Signalraumpunkte s_i umgerechnet werden können, die die Einheit „Wurzel aus Energie” aufweisen.
  
  

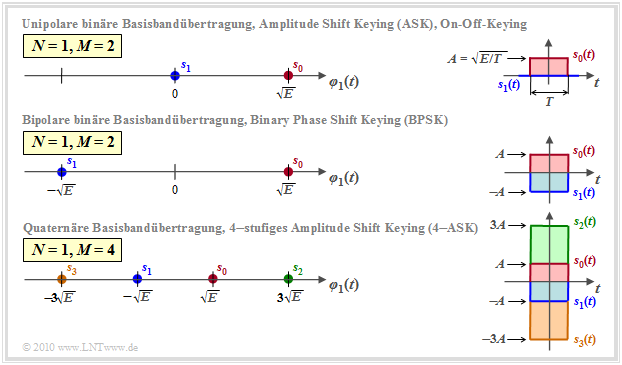
Die Grafik zeigt die Signalraumkonstellationen für die binäre unipolare (oben), die binäre bipolare (Mitte) sowie die quaternäre bipolare (unten) Basisbandübertragung. Rechts sind am Beispiel „Rechteckimpuls” die zwei bzw. vier möglichen Sendesignale s_i(t) angegeben. Man kann daraus auch den Zusammenhang zwischen Signalenergie E und Impulsamplitude A erkennen. Die jeweils linken Darstellungen auf der φ₁–Achse gelten aber unabhängig von der Form des Sendegrundimpulses g_s(t), nicht nur für Rechtecke.

• Die Grafik beschreibt gleichzeitig die eindimensionalen Trägerfrequenzsysteme On–Off–Keying (oben), BPSK bzw. 2–ASK (Mitte) und 4–ASK (unten).
  

• Die Signale s_i(t) und die Basisfunktion φ₁(t) beziehen sich dann auf den äquivalenten TP–Bereich. Im BP–Bereich ist φ₁(t) eine auf den Zeitbereich 0 ≤ t ≤ T begrenzte harmonische Schwingung.
  

Dimension der Basisfunktionen (2)

Zu den zweidimensionalen Modulationsverfahren (N = 2) gehören

• M–stufiges Phase Shift Keying (M–PSK),
  
• Quadratur–Amplitudenmodulation (4–QAM, 16–QAM, 64–QAM, ...),
  
• binäres (orthogonales) Frequency Shift Keying (2–FSK).
  
  

Allgemein ist bei orthogonaler FSK die Anzahl N der Basisfunktionen φ_k(t) gleich der Anzahl M der möglichen Sendesignale s_i(t). N = 2 ist deshalb nur für M = 2 möglich.

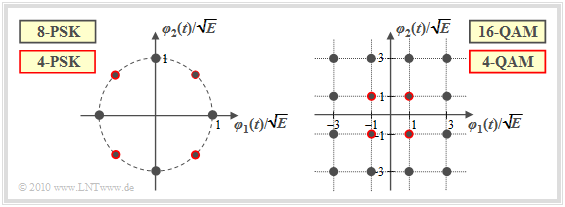
Die linke Grafik zeigt die 8–PSK–Konstellation. Beschränkt man sich auf die rot umrandeten Punkte, so liegt eine 4–PSK (Quaternary Phase Shift Keying, QPSK) vor.

Die rechte Grafik bezieht sich auf die 16–QAM beziehungsweise – wenn man nur die rot umrandeten Signalraumpunkte betrachtet – auf die 4–QAM. Ein Vergleich der beiden Bilder zeigt, dass die 4–QAM mit der QPSK bei entsprechender Achsenskalierung identisch ist.

Die Grafiken beschreiben die Modulationsverfahren sowohl im Bandpass– als auch im äquivalenten Tiefpassbereich:

• Bei der Betrachtung als Bandpass–System sind die Basisfunktionen φ₁(t) und φ₂(t) cosinusförmig bzw. (minus–)sinusförmig – vergleiche hierzu Aufgabe A4.2.
  

• Dagegen ist nach der Transformation der QAM–Systeme in den äquivalenten Tiefpassbereich die Basisfunktion φ₁(t) gleich dem energienormierten (Energie 1) Sendegrundimpuls g_s(t), während φ₂(t) = j · φ₁(t) zu setzen ist. Sie finden Näheres hierzu in der Aufgabe Z4.2.
  

Aufgaben

A4.1 Gram-Schmidt-Verfahren

Zusatzaufgaben:4.1 Andere Basisfunktionen

A4.2 AM/PM-Schwingungen

Zusatzaufgaben:4.2 Achtstufiges Phase Shift Keying

A4.3 Unterschiedliche Frequenzen