Struktur des optimalen Empfängers

1. Digitalsignalübertragung
2. Verallgemeinerte Beschreibung digitaler Modulationsverfahren
3. Struktur des optimalen Empfängers

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

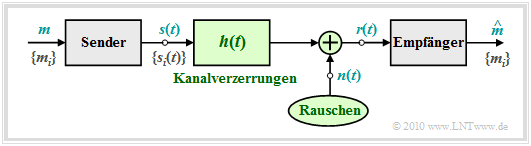
Blockschaltbild und Voraussetzungen

In diesem Kapitel wird die Struktur des optimalen Empfängers eines digitalen Übertragungssystems sehr allgemein hergeleitet, wobei

• das Modulationsverfahren und weitere Systemdetails nicht weiter spezifiziert werden,
  
• von den Basisfunktionen und der Signalraumdarstellung gemäß dem Kapitel Signale, Basisfunktionen und Vektorräume ausgegangen wird.

Allgemeines Blockschaltbild eines Kommunikationssystems

Zum obigen Blockschaltbild ist anzumerken:

• Der Symbolumfang der Quelle beträgt $M$ und der Symbolvorrat ist $\{m_i\}$ mit $i = 0$, ... , $M- 1$. Die zugehörigen Symbolwahrscheinlichkeiten ${\rm Pr}(m = m_i)$ seien auch dem Empfänger bekannt.
  

• Zur Nachrichtenübertragung stehen $M$ verschiedene Signalformen $s_i(t)$ zur Verfügung, wobei für die Laufvariable ebenfalls die Indizierung $i = 0$, ... , $M- 1$ gelten soll. Es besteht eine feste Beziehung zwischen den Nachrichten $\{m_i\}$ und den Signalen $\{s_i(t)\}$. Wird die Nachricht $m =m_i$ übertragen, so ist das Sendesignal $s(t) =s_i(t)$.
  

• Lineare Kanalverzerrungen sind in der obigen Grafik durch die Impulsantwort $h(t)$ berücksichtigt. Außerdem ist ein (irgendwie geartetes) Rauschen $n(t)$ wirksam. Mit diesen beiden die Übertragung störenden Effekten lässt sich das am Empfänger ankommende Signal $r(t)$ in folgender Weise angeben:

$$r(t) = s(t) \star h(t) + n(t) \hspace{0.05cm}.$$

• Aufgabe des (optimalen) Empfängers ist es, anhand seines Eingangssignals $r(t)$ herauszufinden, welche der $M$ möglichen Nachrichten $m_i$ – bzw. welches der Signale $s_i(t)$ – gesendet wurde. Der vom Empfänger gefundene Schätzwert für $m$ wird in Gleichungen durch ein Zirkumflex (französisch: Circonflexe) gekennzeichnet   ⇒   $\hat{m}$.

• Man spricht von einem optimalen Empfänger, wenn die Symbolfehlerwahrscheinlichkeit den für die Randbedingungen kleinstmöglichsten Wert annimmt:

$$p_{\rm S} = {\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm Minimum} \hspace{0.05cm}.$$

Hinweis: Im Folgenden wird meist der AWGN–Ansatz   ⇒   $r(t) = s(t) + n(t)$ vorausgesetzt, was bedeutet, dass $h(t) = \delta(t)$ als verzerrungsfrei angenommen wird. Andernfalls könnten wir die Signale $s_i(t)$ als ${s_i}'(t) = s_i(t) \star h(t)$ neu definieren, also die deterministischen Kanalverzerrungen dem Sendesignal beaufschlagen.

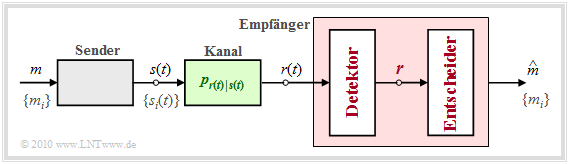
Fundamentaler Ansatz zum optimalen Empfängerentwurf

Gegenüber dem auf der vorherigen Seite gezeigten Blockschaltbild führen wir nun einige wesentliche Verallgemeinerungen durch:

• Der Übertragungskanal wird durch die bedingte Wahrscheinlichkeitsdichtefunktion $p_{\hspace{0.02cm}r(t)\hspace{0.02cm} \vert \hspace{0.02cm}s(t)}$ beschrieben, welche die Anhängigkeit des Empfangssignals $r(t)$ vom Sendesignal $s(t)$ festlegt.
  

• Wurde nun ein ganz bestimmtes Signal $r(t) = \rho(t)$ empfangen, so hat der Empfänger die Aufgabe, anhand dieser Signalrealisierung $\rho(t)$ sowie der $M$ bedingten Wahrscheinlichkeitsdichtefunktionen

$$p_{\hspace{0.02cm}r(t) \hspace{0.02cm} \vert \hspace{0.02cm} s(t) } (\rho(t) | s_i(t))\hspace{0.2cm}{\rm mit}\hspace{0.2cm} i = 0, \text{...} \hspace{0.05cm}, M-1$$

unter Berücksichtigung aller möglichen Sendesignale $s_i(t)$ und deren Auftrittswahrscheinlichkeiten ${\rm Pr}(m = m_i)$ herauszufinden, welche der möglichen Nachrichten $m_i$ bzw. welches der möglichen Signale $s_i(t)$ am wahrscheinlichsten gesendet wurde.

• Die Schätzung des optimalen Empfängers ist also ganz allgemein bestimmt durch die Gleichung

$$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} p_{\hspace{0.02cm}s(t) \hspace{0.02cm} \vert \hspace{0.02cm} r(t) } ( s_i(t) \hspace{0.02cm} \vert \hspace{0.02cm} \rho(t)) = {\rm arg} \max_i \hspace{0.1cm} p_{m | r(t) } ( \hspace{0.02cm}m_i\hspace{0.02cm} \vert \hspace{0.02cm}\rho(t))\hspace{0.05cm},$$

wobei berücksichtigt ist, dass die gesendete Nachricht $m = m_i$ und das gesendete Signal $s(t) = s_i(t)$ eineindeutig ineinander übergeführt werden können.

$\text{In anderen Worten:}$  Der optimale Empfänger betrachtet diejenige Nachricht $m_i$ als die am wahrscheinlichsten gesendete, wenn die bedingte Wahrscheinlichkeitsdichtefunktion $p_{\hspace{0.02cm}m \hspace{0.02cm} \vert \hspace{0.02cm} r(t) }$ für das anliegende Empfangssignal $\rho(t)$ sowie unter der Annahme $m =m_i$ den größtmöglichen Wert annimmt.

Bevor wir die obige Entscheidungsregel näher diskutieren, soll der optimale Empfänger entsprechend der Grafik noch in zwei Funktionsblöcke aufgeteilt werden:

Modell zur Herleitung des optimalen Empfängers

• Der Detektor nimmt am Empfangssignal $r(t)$ verschiedene Messungen vor und fasst diese im Vektor $\boldsymbol{r}$ zusammen. Bei $K$ Messungen entspricht $\boldsymbol{r}$ einem Punkt im $K$–dimensionalen Vektorraum.
  

• Der Entscheider bildet abhängig von diesem Vektor den Schätzwert. Bei einem gegebenen Vektor $\boldsymbol{r} = \boldsymbol{\rho}$ lautet dabei die Entscheidungsregel:

$$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} P_{m | \boldsymbol{ r} } ( m_i | \boldsymbol{\rho}) \hspace{0.05cm}.$$

Im Gegensatz zur oberen Gleichung tritt nun in der Entscheidungsregel eine bedingte Wahrscheinlichkeit P_m|r anstelle der bedingten Wahrscheinlichkeitskeitsdichtefunktion (WDF) p_m|r(t) auf. Beachten Sie bitte die Groß– bzw. Kleinschreibung für die unterschiedlichen Bedeutungen.

Fundamentaler Ansatz zum optimalen Empfängerentwurf (2)

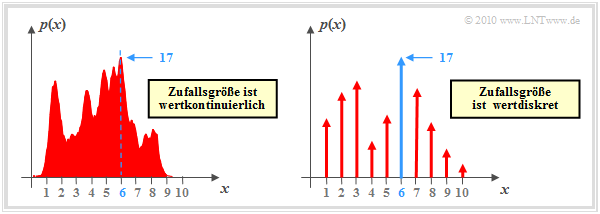
Wir betrachten nun die Funktion y = arg max p(x), wobei p(x) die Wahrscheinlichkeitsdichtefunktion (WDF) einer wertkontinuierlichen oder wertdiskreten Zufallsgröße x beschreibt. Im zweiten Fall besteht die WDF aus einer Summe von Diracfunktionen mit den Wahrscheinlichkeiten als Impulsgewichte.

Die Grafik zeigt beispielhafte Funktionen. In beiden Fällen liegt das WDF–Maximum (17) bei x = 6:

\[\max_i \hspace{0.1cm} p(x) = 17\hspace{0.05cm},\hspace{0.2cm}y = {\rm arg} \max_i \hspace{0.1cm} p(x) = 6\hspace{0.05cm}.\]

Man nennt die (bedingten) Wahrscheinlichkeiten in der Gleichung

\[\hat{m} = {\rm arg} \max_i \hspace{0.1cm} P_{m | \boldsymbol{ r} } ( m_i | \boldsymbol{\rho})\]

auch a–Posteriori–Wahrscheinlichkeiten. Mit dem Satz von Bayes kann hierfür geschrieben werden:

\[P_{m | \boldsymbol{ r} } ( m_i | \boldsymbol{\rho}) = \frac{{\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}|m } (\boldsymbol{\rho}|m_i )}{p_{\boldsymbol{ r}} (\boldsymbol{\rho})} \hspace{0.05cm}.\]

Da der Term im Nenner für alle m_i gleich ist, muss er für die Entscheidung nicht weiter berücksichtigt werden. Damit erhält man die folgenden Regeln:

1: Die Entscheidungsregel des optimalen Empfängers, auch bekannt als MAP–Empfänger (die Abkürzung steht für Maximum–a–posteriori), lautet:

\[\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} P_{m | \boldsymbol{ r} } ( m_i | \boldsymbol{\rho}) = {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}|m } (\boldsymbol{\rho}|m_i )]\hspace{0.05cm}.\]

Der Vorteil dieser Gleichung ist, dass die die Vorwärtsrichtung des Kanals beschreibende bedingte WDF p_r|m („Ausgang unter der Bedingung Eingang”) verwendet werden kann. Dagegen verwendet die erste Gleichung die Rückschlusswahrscheinlichkeiten P_m|r („Eingang unter der Bedingung Ausgang”).

2: Ein Maximum–Likelihood–Empfänger (ML–Empfänger) verwendet die Entscheidungsregel

\[\hat{m}_{\rm ML} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} p_{\boldsymbol{ r}|m } (\boldsymbol{\rho}|m_i )\hspace{0.05cm}.\]

Bei diesem werden die möglicherweise unterschiedlichen Auftrittswahrscheinlichkeiten Pr(m_i) für den Entscheidungsprozess nicht herangezogen, zum Beispiel, weil sie dem Empfänger nicht bekannt sind.

Hinweis: Im Kapitel 3.7 finden Sie eine andere Herleitung. Allgemein gilt: Bei gleichwahrscheinlichen Nachrichten {m_i}  ⇒  Pr(m_i) = 1/M ist der ML–Empfänger gleichwertig mit dem MAP–Empfänger:

\[\hat{m}_{\rm MAP} = \hat{m}_{\rm ML} =\hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} p_{\boldsymbol{ r}|m } (\boldsymbol{\rho}|m_i )\hspace{0.05cm}.\]

Das Theorem der Irrelevanz (1)

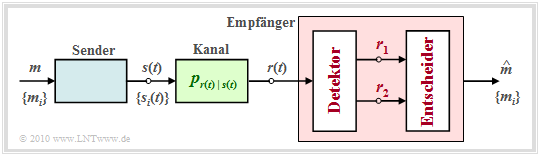
Zu beachten ist, dass der auf der letzten Seite beschriebene Empfänger nur dann optimal ist, wenn auch der Detektor bestmöglich implementiert ist, das heißt, wenn durch den Übergang vom kontinuierlichen Signal r(t) zum Vektor r  keine Information verloren geht.

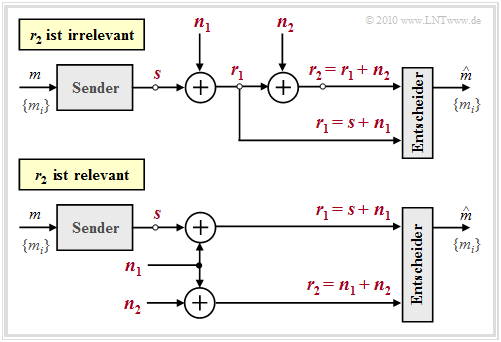
Um die Frage zu klären, welche und wieviele Messungen am Empfangssignal r(t) durchzuführen sind, um Optimalität zu garantieren, ist das Theorem der Irrelevanz hilfreich. Dazu betrachten wir den nachfolgend skizzierten Empfänger, dessen Detektor aus dem Empfangssignal r(t) die zwei Vektoren r₁ und r₂ ableitet und dem Entscheider zur Verfügung stellt. r₁ und r₂ stehen mit der Nachricht m ∈ {m_i} über die Verbundwahrscheinlichkeitsdichte p_{r1, r2|m} in Zusammenhang.

Zum Theorem der Irrelevanz

Die Entscheidungsregel des MAP–Empfängers lautet mit Anpassung an dieses Beispiel:

\[\hat{m}_{\rm MAP} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 , \hspace{0.05cm}\boldsymbol{ r}_2 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1, \hspace{0.05cm}\boldsymbol{\rho}_2|m_i )]=\]

\[\hspace{-0.1cm} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1 |m_i ) \cdot p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )] \hspace{0.05cm}.\]

Hierzu ist anzumerken:

• Die Vektoren r₁ und r₂ sind Zufallsgrößen. Ihre Realisierungen werden hier und im Folgenden mit ρ₁ und ρ₂ bezeichnet. Zur Hervorhebung sind alle Vektoren in der Grafik rot eingetragen.
• Die Voraussetzungen für die Anwendung des „Theorems der Irrelevanz” sind die gleichen wie die an eine Markovkette erster Ordnung. Die Zufallsvariablen x, y, z formen dann eine solche, falls die Verteilung von z bei gegebenem y unabhängig von x ist:

\[p(x, y, z) = p(x) \cdot p(y|x) \cdot p(z|y) \hspace{0.25cm} {\rm anstelle \hspace{0.15cm}von} \hspace{0.25cm}p(x, y, z) = p(x) \cdot p(y|x) \cdot p(z|x, y) \hspace{0.05cm}.\]

• Der optimale Empfänger muss im allgemeinen Fall beide Vektoren r₁ und r₂ auswerten, da in obiger Entscheidungsregel beide Verbundwahrscheinlichkeitsdichten p_r1|m und p_{r2| r1, m} auftreten.

• Dagegen kann der Empfänger ohne Informationseinbuße die zweite Messung vernachlässigen, falls r₂ bei gegebenem r₁ unabhängig von der Nachricht m ist:

\[p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 ) \hspace{0.05cm}.\]

• In diesem Fall lässt sich die Entscheidungsregel weiter vereinfachen:

\[\hat{m}_{\rm MAP} \hspace{-0.1cm} = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1 |m_i ) \cdot p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )]= \]

\[ = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1 |m_i ) \cdot p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 )]=\]

\[ = \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r}_1 |m } \hspace{0.05cm} (\boldsymbol{\rho}_1 |m_i ) ] \hspace{0.05cm}.\]

Das Theorem der Irrelevanz (2)

Betrachten wir zur Verdeutlichung des soeben vorgestellten Theorems der Irrelevanz zwei verschiedene Systemkonfigurationen mit jeweils zwei Rauschtermen n₁ und n₂. Anmerkung: Alle vektoriellen Größen sind rot eingezeichnet und s, n₁ und n₂ seien jeweils unabhängig voneinander.

Die Analyse dieser beiden Anordnungen liefert folgende Ergebnisse:

• Der Entscheider muss in beiden Fällen die Komponente r₁ = s + n₁ berücksichtigen, da nur diese die Information über das Nutzsignal s und damit über die gesendete Nachricht m liefert.
  

• Bei der oberen Konfiguration enthält r₂ keine Information über m, die nicht bereits von r₁ geliefert wurde. Vielmehr ist r₂ = r₁ + n₂ nur eine verrauschte Version von r₁ und hängt nur vom Rauschen n₂ ab, sobald r₁ bekannt ist  ⇒  r₂ ist irrelevant:

\[p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i )= p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 )= p_{\boldsymbol{ n}_2 } \hspace{0.05cm} (\boldsymbol{\rho}_2 - \boldsymbol{\rho}_1 )\hspace{0.05cm}.\]

• Bei der unteren Konfiguration ist dagegen r₂ = n₁ + n₂ für den Empfänger hilfreich, da dadurch dem Empfänger ein Schätzwert für den Rauschterm n₁ geliefert wird  ⇒  r₂ sollte nicht verworfen werden. Formal lässt sich dieses Resultat wie folgt ausdrücken:

\[p_{\boldsymbol{ r}_2 | \boldsymbol{ r}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2| \boldsymbol{\rho}_1 , \hspace{0.05cm}m_i ) \hspace{-0.1cm} = \hspace{-0.1cm} p_{\boldsymbol{ r}_2 | \boldsymbol{ n}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2 | \boldsymbol{\rho}_1 - \boldsymbol{s}_i, \hspace{0.05cm}m_i)= \]

\[ \hspace{0.5cm} \hspace{-0.1cm} = \hspace{-0.1cm} p_{\boldsymbol{ n}_2 | \boldsymbol{ n}_1 , \hspace{0.05cm} m } \hspace{0.05cm} (\boldsymbol{\rho}_2- \boldsymbol{\rho}_1 + \boldsymbol{s}_i| \boldsymbol{\rho}_1 - \boldsymbol{s}_i, \hspace{0.05cm}m_i)= \]

\[\hspace{0.4cm}=\hspace{-0.1cm} p_{\boldsymbol{ n}_2 } \hspace{0.05cm} (\boldsymbol{\rho}_2- \boldsymbol{\rho}_1 + \boldsymbol{s}_i ) \hspace{0.05cm}.\]

Da nun im Argument dieser Funktion die Nachricht (s_i) erscheint, ist r₂ nicht irrelevant.

Einige Eigenschaften des AWGN-Kanals (1)

Um weitere Aussagen über die Art der optimalen Messungen des Vektors r  machen zu können, ist es notwendig, die den Kanal charakterisierende (bedingte) Wahrscheinlichkeitsdichtefunktion p_r(t)|s(t) weiter zu spezifizieren. Im Folgenden wird die Kommunikation über den AWGN–Kanal betrachtet, dessen wichtigste Eigenschaften hier nochmals kurz zusammengestellt werden:

• Das Ausgangssignal des AWGN–Kanals ist r(t) = s(t) + n(t), wobei s(t) das Sendesignal angibt und n(t) durch einen Gaußschen Rauschprozess dargestellt wird.
  

• Ein Zufallsprozess {n(t)} ist gaußisch, falls die Elemente der k–dimensionalen Zufallsvariablen {n(t₁), ... , n(t_k)} gemeinsam gaußverteilt sind („Jointly Gaussian”).
  

• Der Mittelwert des AWGN–Rauschens ist E[n(t)] = 0. Außerdem ist n(t) weiß, was bedeutet, dass das Leistungsdichtespektrum (LDS) für alle Frequenzen (von – ∞ bis + ∞) konstant ist:

\[{\it \Phi_n(f)} = {N_0}/{2} \hspace{0.05cm}.\]

• Nach dem Wiener–Chintchine–Theorem ergibt sich die Autokorrelationsfunktion (AKF) als die Fourierrücktransformierte von Φ_n(f):

\[{\varphi_n(\tau)} = {\rm E}[n(t) \cdot n(t+\tau) ] = {N_0}/{2} \cdot \delta(t)\]

\[\Rightarrow \hspace{0.3cm} {\rm E}[n(t) \cdot n(t+\tau) ] = \left\{ \begin{array}{c} \rightarrow \infty \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f{\rm \ddot{u}r}} \hspace{0.15cm} \tau = 0 \hspace{0.05cm}, \\ {\rm f{\rm \ddot{u}r}} \hspace{0.15cm} \tau \ne 0 \hspace{0.05cm},\\ \end{array}\]

• N₀ gibt dabei die physikalische (nur für f ≥ 0 definierte) Rauschleistungsdichte an. Der konstante LDS–Wert (N₀/2) und das Gewicht der Diracfunktion in der AKF (ebenfalls N₀/2) ergibt sich allein durch die zweiseitige Betrachtungsweise.
  
  

Weitere Informationen zum AWGN–Kanal liefert das Lernvideo Der AWGN–Kanal – Teil 2.

Einige Eigenschaften des AWGN-Kanals (2)

Aus dem vorletzten Statement auf der letzten Seite geht hervor, dass

• reines AWGN–Rauschen n(t) stets eine unendliche Varianz (Leistung) aufweist: σ_n² → ∞,
  
• in der Realität demzufolge nur gefiltertes Rauschen n'(t) = n(t) ∗ h_n(t) auftreten kann.
  
  

Mit der Impulsantwort h_n(t) und dem Frequenzgang H_n(f) = F[h_n(t)] gelten dann folgende Gleichungen:

\[{\rm E}[n'(t) ] \hspace{0.15cm} = \hspace{0.2cm} {\rm E}[n(t) ] = 0 \hspace{0.05cm},\] \[\hspace{0.4cm}{\it \Phi_{n'}(f)} \hspace{0.1cm} = \hspace{0.1cm} {N_0}/{2} \cdot |H_{n}(f)|^2 \hspace{0.05cm},\] \[ \hspace{0.4cm}{\it \varphi_{n'}(\tau)} \hspace{0.1cm} = \hspace{0.1cm} {N_0}/{2}\hspace{0.1cm} \cdot [h_{n}(\tau) \star h_{n}(-\tau)]\hspace{0.05cm},\]

\[\hspace{0.4cm}\sigma_n^2 \hspace{0.1cm} = \hspace{0.1cm} { \varphi_{n'}(\tau = 0)} = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}h_n^2(t)\,{\rm d} t ={N_0}/{2}\hspace{0.1cm} \cdot < \hspace{-0.1cm}h_n(t), \hspace{0.1cm} h_n(t) \hspace{-0.05cm} > \hspace{0.1cm}=\]

\[\hspace{0.6cm}\hspace{-0.1cm} = \hspace{0.1cm} \int_{-\infty}^{+\infty}{\it \Phi_{n'}(f)}\,{\rm d} f = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|H_n(f)|^2\,{\rm d} f \hspace{0.05cm}.\]

Im Folgenden beinhaltet n(t) stets implizit eine Bandbegrenzung; auf die Schreibweise n'(t) wird also zukünftig verzichtet.

Ähnlich wie das Sendesignal s(t) lässt sich auch der Rauschprozess n(t) als gewichtete Summe von orthonormalen Basisfunktionen φ_j(t) schreiben. Im Gegensatz zu s(t) ist allerdings nun eine Beschränkung auf eine endliche Anzahl an Basisfunktionen nicht möglich. Vielmehr gilt bei rein stochastischen Größen

\[n(t) = \lim_{N \rightarrow \infty} \sum\limits_{j = 1}^{N}n_j \cdot \varphi_j(t) \hspace{0.05cm},\]

wobei der Koeffizient n_j durch die Projektion von n(t) auf die Basisfunktion φ_j(t) bestimmt ist:

\[n_j = \hspace{0.1cm} < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.05cm}.\]

Hinweis: Um eine Verwechslung mit den Basisfunktionen φ_j(t) zu vermeiden, wird im Folgenden die AKF φ_n(τ) des Rauschprozesses stets nur noch als der Erwartungswert E[n(t) · n(t + τ)] ausgedrückt.

Optimaler Empfänger für den AWGN-Kanal (1)

Auch das Empfangssignal r(t) = s(t) + n(t) lässt sich in bekannter Weise in Basisfunktionen zerlegen: \[r(t) = \sum\limits_{j = 1}^{\infty}r_j \cdot \varphi_j(t) \hspace{0.05cm}.\]

Zu berücksichtigen ist:

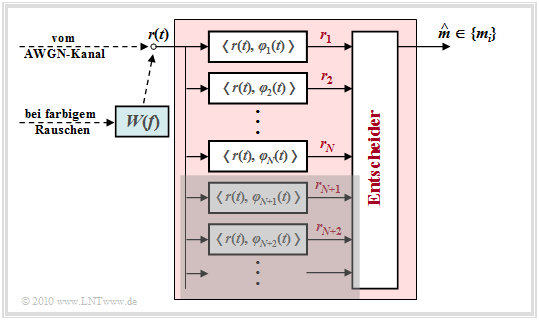
• Die M möglichen Sendesignale {s_i(t)} spannen einen Signalraum mit insgesamt N Basisfunktionen φ₁(t), ... , φ_N(t) auf.
  

• Diese N Basisfunktionen φ_j(t) werden gleichzeitig zur Beschreibung des Rauschsignals n(t) und des Empfangssignals r(t) verwendet.
  

• Zur vollständigen Charakterisierung von n(t) bzw. r(t) werden nun aber darüber hinaus noch unendlich viele weitere Basisfunktionen φ_N+1(t), φ_N+2(t), ... benötigt.
  

• Damit ergeben sich die Koeffizienten des Empfangssignals r(t) gemäß folgender Gleichung, wobei berücksichtigt ist, dass die Signale s_i(t) und das Rauschen n(t) voneinander unabhängig sind:

\[r_j \hspace{0.1cm} = \hspace{0.1cm} \hspace{0.1cm} < \hspace{-0.1cm}r(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm}=\]

\[ \hspace{-0.1cm} = \hspace{-0.1cm} \left\{ \begin{array}{c} < \hspace{-0.1cm}s_i(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > + < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm}= s_{ij}+ n_j\\ < \hspace{-0.1cm}n(t), \hspace{0.1cm} \varphi_j(t) \hspace{-0.05cm} > \hspace{0.1cm} = n_j \end{array} \right.\quad \begin{array}{*{1}c} {j = 1, 2, ... \hspace{0.05cm}, N} \hspace{0.05cm}, \\ {j > N} \hspace{0.05cm}.\\ \end{array}\]

Somit ergibt sich für den optimalen Empfänger die folgende Struktur.

Optimaler Empfänger beim AWGN-Kanal

Die Bildbeschreibung folgt auf der nächsten Seite.

Optimaler Empfänger für den AWGN-Kanal (2)

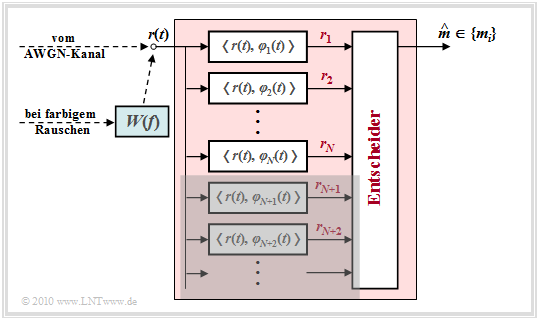
Betrachten wir zunächst wieder den AWGN–Kanal. Hier kann auf das Vorfilter mit dem Frequenzgang W(f) verzichtet werden, das in der Grafik für farbiges Rauschen vorgesehen ist.

Der Detektor des optimalen Empfängers bildet die Koeffizienten r_j = 〈r(t), φ_j(t)〉 und reicht diese an den Entscheider weiter. Basiert die Entscheidung auf sämtlichen – also unendlich vielen – Koeffizienten r_j, so ist die Wahrscheinlichkeit für eine Fehlentscheidung minimal und der Empfänger optimal.

Die reellwertigen Koeffizienten r_j wurden auf der letzten Seite wie folgt berechnet:

\[r_j = \left\{ \begin{array}{c} s_{ij} + n_j\\ n_j \end{array} \right.\quad \begin{array}{*{1}c} {j = 1, 2, ... \hspace{0.05cm}, N} \hspace{0.05cm}, \\ {j > N} \hspace{0.05cm}.\\ \end{array}\]

Nach dem Theorem der Irrelevanz lässt sich zeigen, dass für additives weißes Gaußsches Rauschen

• die Optimalität nicht herabgesetzt wird, wenn man die nicht von der Nachricht (s_ij) abhängigen Koeffizienten r_N+1, r_N+2, ... nicht in den Entscheidungsprozess einbindet, und somit
  

• der Detektor nur die Projektionen des Empfangssignals r(t) auf die N durch das Nutzsignal s(t) vorgegebenen Basisfunktionen φ₁(t), ... , φ_N(t) bilden muss.
  

In der Grafik ist diese signifikante Vereinfachung durch die graue Hinterlegung angedeutet.

Im Fall von farbigem Rauschen   ⇒   Leistungsdichtespektrum Φ_n(f) ≠ const. ist lediglich zusätzlich ein Vorfilter mit dem Amplitudengang

\[|W(f)| = \frac{1}{\sqrt{\it \Phi_n(f)}}\]

erforderlich. Man nennt dieses Filter auch „Whitening Filter”, da die Rauschleistungsdichte am Ausgang wieder konstant, also „weiß” ist. Genaueres hierzu finden Sie im Kapitel 5.4 des Buches „Stochastische Signaltheorie”.

Implementierungsaspekte

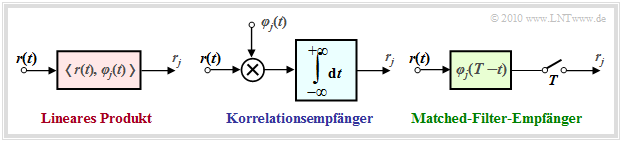
Wesentliche Bestandteile des optimalen Empfängers sind die Berechnungen der inneren Produkte gemäß den Gleichungen r_j = 〈r(t), φ_j(t)〉. Diese können auf verschiedene Art und Weise implementiert werden:

• Beim Korrelationsempfänger (Näheres zu dieser Implementierung finden Sie im Kapitel 3.7) werden die inneren Produkte direkt entsprechend der Definition mit analogen Multiplizierern und Integratoren realisiert:

\[r_j = \int_{-\infty}^{+\infty}r(t) \cdot \varphi_j(t) \,{\rm d} t \hspace{0.05cm}.\]

• Der Matched–Filter–Empfänger, der bereits im Kapitel 1.2 dieses Buches hergeleitet wurde, erzielt mit einem linearen Filter mit der Impulsantwort h_j(t) = φ_j(T – t) und anschließender Abtastung zum Zeitpunkt t = T das gleiche Ergebnis:

\[r_j = \int_{-\infty}^{+\infty}r(\tau) \cdot h_j(t-\tau) \,{\rm d} \tau = \int_{-\infty}^{+\infty}r(\tau) \cdot \varphi_j(T-t+\tau) \,{\rm d} \tau \]

\[\Rightarrow \hspace{0.3cm} r_j (t = \tau) = \int_{-\infty}^{+\infty}r(\tau) \cdot \varphi_j(\tau) \,{\rm d} \tau = r_j \hspace{0.05cm}.\]

Implementierungen des inneren Produktes

Die Abbildung zeigt die beiden möglichen Realisierungsformen des optimalen Detektors. Bevor wir uns im folgenden Kapitel der optimalen Gestaltung des Entscheiders und der Berechnung und Annäherung der Fehlerwahrscheinlichkeit zuwenden, erfolgt zunächst eine für den AWGN–Kanal gültige statistische Analyse der Entscheidungsgrößen r_j.

Wahrscheinlichkeitsdichtefunktion der Empfangswerte

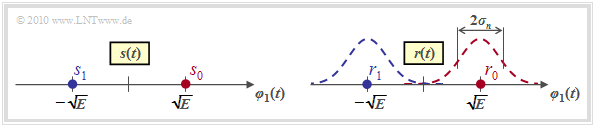
Betrachten wir nochmals den optimalen Binärempfänger für die bipolare Basisbandübertragung über den AWGN–Kanal, wobei wir von der für Kapitel 4 gültigen Beschreibungsform ausgehen. Bei N = 1 und M = 2 ergibt sich für das Sendesignal die in der linken Grafik dargestellte Signalraumkonstellation

• mit nur einer Basisfunktion φ₁(t), wegen N = 1,
  
• mit den beiden Signalraumpunkten s_i ∈ {s₀, s₁}, wegen M = 2.
  
  

Signalraumkonstellation und WDF des Empfangssignals

Für das Signal am Ausgang des AWGN–Kanals,

\[r(t) = s(t) + n(t) \hspace{0.05cm},\]

ergibt sich im rauschfreien Fall ⇒ r(t) = s(t) die genau gleiche Konstellation; die Signalraumpunkte liegen somit bei

\[r_0 = s_0 = \sqrt{E}\hspace{0.05cm},\hspace{0.2cm}r_1 = s_1 = -\sqrt{E}\hspace{0.05cm}.\]

Bei Berücksichtigung des (bandbegrenzten) AWGN–Rauschens n(t) überlagern sich den beiden Punkten r₀ und r₁ jeweils Gaußkurven mit der Varianz σ_n²  ⇒  Streuung σ_n (siehe rechte Grafik). Die WDF der Rauschkomponente n lautet dabei:

\[p_n(n) = \frac{1}{\sqrt{2\pi} \cdot \sigma_n}\cdot {\rm exp} \left [ - \frac{n^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}.\]

Für die bedingte Wahrscheinlichkeitsdichte, dass der Empfangswert ρ anliegt, wenn s_i gesendet wurde, ergibt sich dann folgender Ausdruck:

\[p_{r|s}(\rho|s_i) = \frac{1}{\sqrt{2\pi} \cdot \sigma_n}\cdot {\rm exp} \left [ - \frac{(\rho - s_i)^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}.\]

Zu den Einheiten der hier aufgeführten Größen ist zu bemerken:

• r₀ = s₀, r₁ = s₁ sowie n sind jeweils Skalare mit der Einheit „Wurzel aus Energie”.
  

• Damit ist offensichtlich, dass σ_n ebenfalls die Einheit „Wurzel aus Energie” besitzt und σ_n² eine Energie darstellt.
  

• Beim AWGN–Kanal ist die Rauschvarianz σ_n² = N₀/2. Diese ist also ebenfalls eine physikalische Größe mit der Einheit W/Hz = Ws.
  
  

Die hier angesprochene Thematik wird in der Aufgabe A4.6 an Beispielen verdeutlicht.

N–dimensionales Gaußsches Rauschen (1)

Liegt ein N–dimensionales Modulationsverfahren vor, das heißt, es gilt mit 0 ≤ i ≤ M –1 und 1 ≤ j ≤ N:

\[s_i(t) = \sum\limits_{j = 1}^{N} s_{ij} \cdot \varphi_j(t) = s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) + ... + s_{iN} \cdot \varphi_N(t)\hspace{0.05cm} \]

\[\Rightarrow \hspace{0.3cm} \boldsymbol{ s}_i = \left(s_{i1}, s_{i2}, ... \hspace{0.05cm}, s_{iN}\right ) \hspace{0.05cm},\]

so muss der Rauschvektor n ebenfalls mit der Dimension N angesetzt werden, und das gleiche gilt auch für den Empfangsvektor r :

\[\boldsymbol{ n} = \left(n_{1}, n_{2}, ... \hspace{0.05cm}, n_{N}\right ) \hspace{0.01cm},\hspace{0.2cm}\boldsymbol{ r} = \left(r_{1}, r_{2}, ... \hspace{0.05cm}, r_{N}\right )\hspace{0.05cm}.\]

Die Wahrscheinlichkeitsdichtefunktion (WDF) lautet dann für den AWGN–Kanal mit der Realisierung η des Rauschsignals

\[p_{\boldsymbol{ n}}(\boldsymbol{ \eta}) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^N } \cdot {\rm exp} \left [ - \frac{|| \boldsymbol{ \eta} ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm},\]

und für die bedingte WDF in der ML–Entscheidungsregel ist anzusetzen:

\[p_{\boldsymbol{ r}\hspace{0.05cm} | \hspace{0.01cm} \boldsymbol{ s}}(\boldsymbol{ \rho} | \boldsymbol{ s}_i) \hspace{-0.1cm} = \hspace{0.1cm} p_{\boldsymbol{ n}\hspace{0.05cm} | \hspace{0.01cm} \boldsymbol{ s}}(\boldsymbol{ \rho} - \boldsymbol{ s}_i| \boldsymbol{ s}_i) =\]

\[\hspace{-0.05cm} = \hspace{-0.1cm} \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot {\rm exp} \left [ - \frac{|| \boldsymbol{ \rho} - \boldsymbol{ s}_i ||^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}.\]

Die Gleichung ergibt sich aus der allgemeinen Darstellung der N–dimensionalen Gaußschen WDF in Kapitel 4.7 des Buches „Stochastische Signaltheorie” unter der Voraussetzung, dass die Komponenten unkorreliert (und somit statistisch unabhängig) sind. ||η|| bezeichnet man als die Norm (Länge) des Vektors η.

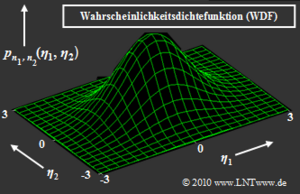
Dargestellt ist die zweidimensionale Gauß–WDF p_n(η) der 2D–Zufallsgröße n = (n₁, n₂). Die Bildbeschreibung folgt auf der nächsten Seite.

N–dimensionales Gaußsches Rauschen (2)

Zweidimensionale Gauß–WDF

Zu der dargestellten 2D–WDF ist anzumerken:

• Die Dichtefunktion bezieht sich auf die Zufallsgröße n = (n₁, n₂). Realisierungen hiervon werden mit η = (η₁, η₂) bezeichnet. Die Gleichung der dargestellten Glockenkurve lautet:

\[p_{n_1, n_2}(\eta_1, \eta_2) = \frac{1}{\left( \sqrt{2\pi} \cdot \sigma_n \right)^2 } \cdot {\rm exp} \left [ - \frac{ \eta_1^2 + \eta_2^2}{2 \sigma_n^2}\right ]\hspace{0.05cm}. \]

• Das Maximum dieser Funktion liegt bei η₁ = η₂ = 0 und hat den Wert 2π · σ_n². Mit σ_n² = N₀/2 lässt sich die 2D–WDF in Vektorform auch wie folgt schreiben:

\[p_{\boldsymbol{ n}}(\boldsymbol{ \eta}) = \frac{1}{\pi \cdot N_0 } \cdot {\rm exp} \left [ - \frac{|| \boldsymbol{ \eta} ||^2}{N_0}\right ]\hspace{0.05cm}.\]

• Diese rotationssymmetrische WDF eignet sich zum Beispiel für die Beschreibung/Untersuchung eines linearen zweidimensionalen Modulationsverfahrens wie QAM, M–PSK oder 2–FSK.
  

• Oft werden zweidimensionale reelle Zufallsgrößen aber auch eindimensional–komplex dargestellt, meist in der Form n(t) = n_I(t) + j · n_Q(t). Die beiden Komponenten bezeichnet man dann als Inphaseanteil n_I und Quadraturanteil n_Q des Rauschens.
  

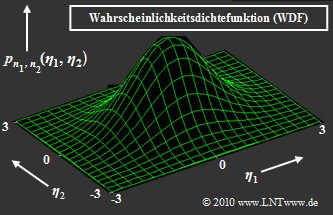
• Die Wahrscheinlichkeitsdichtefunktion hängt nur vom Betrag |n(t)| der Rauschvariablen ab und nicht von Winkel arc n(t). Das heißt: Komplexes Rauschen ist zirkulär symmetrisch (siehe Grafik).
  

• Zirkulär symmetrisch bedeutet auch, dass Inphasekomponente n_I und Quadraturkomponente n_Q die gleiche Verteilung aufweisen und damit auch gleiche Varianz (Streuung) besitzen:

\[ \hspace{0.38cm}{\rm E}\left [ n_{\rm I}^2(t)\right ]\hspace{0.1cm}\hspace{-0.1cm} = \hspace{0.1cm}\hspace{-0.1cm} {\rm E}\left [ n_{\rm Q}^2(t)\right ] = \sigma_n^2 \hspace{0.05cm},\]

\[{\rm E}\left [ n(t) \cdot n^*(t) \right ]\hspace{0.1cm} = \hspace{0.1cm} = {\rm E}\left [ n_{\rm I}^2(t)\right ] + {\rm E}\left [ n_{\rm Q}^2(t)\right ] = 2\sigma_n^2 \hspace{0.05cm}.\]

Abschließend noch einige Beschreibungsformen für Gaußsche Zufallsgrößen:

\[x \hspace{-0.1cm} = \hspace{-0.1cm}{\cal N}(\mu, \sigma^2) \hspace{-0.1cm}: \hspace{0.3cm}{\rm reelle \hspace{0.15cm} gaussverteilte \hspace{0.15cm}ZG}\hspace{0.05cm}, {\rm \hspace{0.15cm}Mittelwert\hspace{0.15cm}}\mu {\rm , \hspace{0.15cm}Varianz\hspace{0.15cm}}\sigma^2 \hspace{0.05cm},\] \[y \hspace{-0.1cm} = \hspace{-0.1cm}{\cal CN}(\mu, \sigma^2)\hspace{-0.1cm}: \hspace{0.07cm}{\rm komplexe \hspace{0.15cm}gaussverteilte \hspace{0.15cm}ZG} \hspace{0.05cm}.\]

Aufgaben zum Kapitel

A4.4 MAP– und ML–Empfänger

A4.5 Theorem der Irrelevanz