Aufgabe 1.3: Rayleigh–Fading

Rayleigh–Fading ist anzuwenden, wenn es

zwischen Sender und Empfänger keine Direktverbindung gibt, und
das Signal den Empfänger auf vielen Wegen erreicht, aber deren Laufzeiten näherungsweise gleich sind.

Ein Beispiel eines solchen Rayleigh–Kanals tritt beim Mobilfunk im städtischen Gebiet auf, wenn schmalbandige Signale verwendet werden mit Reichweiten zwischen 50 und 100 m.

Betrachtet man die Funksignale s(t) und r(t) im äquivalenten Tiefpassbereich (das heißt, um die Frequenz <nobr>f = 0),</nobr> so wird die Signalübertragung durch die Gleichung

$$r(t)= z(t) \cdot s(t)$$

vollständig beschrieben. Die multiplikative Verfälschung

$$z(t)= x(t) + {\rm j} \cdot y(t)$$

ist stets komplex und weist folgende Eigenschaften auf:

Der Realteil x(t) und der Imaginärteil y(t) sind Gaußsche mittelwertfreie Zufallsgrößen, beide mit gleicher Varianz σ². Innerhalb der Komponenten x(t) und y(t) kann es statistische Bindungen geben, was aber für die Lösung der vorliegenden Aufgabe nicht relevant ist. Es bestehen keine Bindungen zwischen x(t) und y(t); deren Kreuzkorrelationsfunktion ist identisch Null.
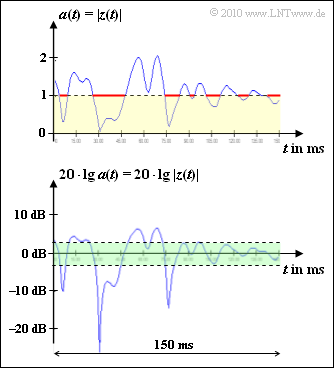
Der Betrag a(t) = |z(t)| besitzt eine Rayleigh–WDF, woraus sich der Name „Rayleigh–Fading” ableitet:

$$f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm exp} [ -a^2/(2\sigma^2)] \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} a \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} a < 0 \\ \end{array} \hspace{0.05cm}.$$

Fragebogen

Musterlösung

1. 2. 3. 4. 5. 6. 7.

	Falsch
	Richtig