Aufgabe 3.3Z: Optimierung eines Koaxialkabelsystems

• Zurück zum Buch

Tabelle: Augenöffnung $\ddot{o}(T_{\rm D})$, Detektionsrauscheffektivwert $\sigma_{\rm d}$ – jeweils normiert auf die Sendeamplitude $s_0$ – für verschiedene Grenzfrequenzen $f_{\rm G}$

Wir betrachten ein redundanzfreies binäres Übertragungssystem mit folgenden Spezifikationen:

• Die Sendeimpulse sind NRZ–rechteckförmig und besitzen die Energie $E_{\rm B} = s_0^2 \cdot T$.
• Der Kanal ist ein Koaxialkabel mit der charakteristischen Kabeldämpfung $a_* = 40 \, {\rm dB}$.
• Es liegt AWGN–Rauschen mit der Rauschleistungsdichte $N_0 = 0.0001 \cdot E_{\rm B}$ vor.
• Der Empfängerfrequenzgang $H_{\rm E}(f)$ beinhaltet einen idealen Kanalentzerrer $H_{\rm K}^{\rm -1}(f)$ und einen Gaußtiefpass $H_{\rm G}(f)$ mit Grenzfrequenz $f_{\rm G}$ zur Rauschleistungsbegrenzung.

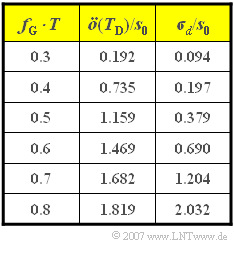
Die Tabelle zeigt die Augenöffnung $\ddot{o}(T_{\rm D})$ sowie den Detektionsrauscheffektivwert $\sigma_{\rm d}$ – jeweils normiert auf die Sendeamplitude $s_0$ – für verschiedene Grenzfrequenzen $f_{\rm G}$. Die Grenzfrequenz ist so zu wählen, dass die ungünstigste Fehlerwahrscheinlichkeit

$$p_{\rm U} = {\rm Q} \left( \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d} \right) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}}\right)$$

möglichst klein ist. Die ungünstigste Fehlerwahrscheinlichkeit stellt eine obere Schranke für die mittlere Fehlerwahrscheinlichkeit $p_{\rm S}$ dar. Für $f_{\rm G} \cdot T ≥ 0.4$ kann auch eine untere Schranke angegeben werden:

$${1}/{4} \cdot p_{\rm U}\le p_{\rm S}\le p_{\rm U} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Themengebiet von Berücksichtigung von Kanalverzerrungen und Entzerrung.
• Zur numerischen Auswertung der Q–Funktion können Sie das folgende Interaktionsmodul nutzen: Gaußsche Fehlerfunktion

Fragebogen

1

Bestimmen Sie innerhalb des vorgegebenen Rasters die optimale Grenzfrequenz hinsichtlich des Kriteriums "ungünstigste Fehlerwahrscheinlichkeit".

$f_{\rm G, opt} \cdot T$ =

2

Welche Werte ergeben sich damit für den ungünstigsten Störabstand und die ungünstigste Fehlerwahrscheinlichkeit?

$f_{\rm G, opt}: 10 \cdot {\rm lg} \, \rho_{\rm U}$ = ${\rm dB}$

$f_{\rm G, opt}: p_{\rm U}$ = $10^{\rm -2}$

3

Wie müsste man die Rauschleistungsdichte $N_0$ (bezogen auf die Signalenergie) verringern, damit $p_{\rm U}$ nicht größer ist als $10^{\rm -6}$?

$N_0/E_{\rm B}$ = $10^{\rm -5}$

4

Geben Sie für den unter c) getroffenen Annahmen eine untere und eine obere Schranke für die mittlere Fehlerwahrscheinlichkeit $p_{\rm S}$ an.

$p_{\rm S, min}$ = $10^{\rm -6}$

$p_{\rm S, max}$ = $10^{\rm -6}$

Musterlösung

Musterlösung

(1)  Für die Optimierung genügt es , den Quotienten $\ddot{o}(T_{\rm D})/\sigma_d$ zu maximieren. Dieser ist von den in der Tabelle gegebenen Werten für die Grenzfrequenz $f_{\rm G, opt} \cdot T = \underline {= 0.4}$ mit $0.735/0.197 \approx 3.73$ maximal. Zum Vergleich: Für $f_{\rm G} \cdot T = 0.3$ ergibt sich aufgrund der kleineren Augenöffnung $0.192/0.094 \approx 2.04$ und für $f_{\rm G} \cdot T = 0.5$ ist der Quotient ebenfalls kleiner als beim Optimum: $1.159/0.379 \approx 3.05$.

Eine noch größere Grenzfrequenz führt zu einem sehr großen Störeffektivwert, ohne dass gleichzeitig die vertikale Augenöffnung in gleicher Weise vergrößert wird.

(2)  Mit dem Ergebnis aus 1) erhält man weiter:

$$\rho_{\rm U} = \left ( {3.73}/{2} \right )^2 \approx 3.48 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline { = 5.41\,{\rm dB}}$$

$$\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q}\left ( {3.73}/{2} \right) \hspace{0.15cm}\underline {\approx 0.031} \hspace{0.05cm}.$$

(3)  Mit dem gegebenen $10 \cdot {\rm lg} \, E_{\rm B}/N_0 = 40 \ \rm dB$, also $E_{\rm B}/N_0 = 10^4$ hat sich der ungünstigste Störabstand zu $10 \cdot {\rm lg} \, \rho_{\rm U} \approx 5.41 \, {\rm dB}$ ergeben. Für die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U} = 10^{\rm -6}$ muss aber $10 \cdot {\rm lg} \, \rho_{\rm U} > 13.55 \, {\rm dB}$ sein. Dies erreicht man, indem man den Quotienten $E_{\rm B}/N_0$ entsprechend erhöht:

$$10 \cdot {\rm lg}\hspace{0.1cm}{E_{\rm B}}/{N_0} = 40\,{\rm dB} \hspace{0.1cm}+\hspace{0.1cm}13.55\,{\rm dB} \hspace{0.1cm}-\hspace{0.1cm}5.41\,{\rm dB}= 48.14\,{\rm dB}$$

$$\Rightarrow \hspace{0.3cm} {E_{\rm B}}/{N_0} = 10^{4.814}\approx 65163 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {N_0}/{E_{\rm B}}\hspace{0.15cm}\underline { = 1.53 \cdot 10^{-5}} \hspace{0.05cm}.$$

(4)  Die obere Schranke für $p_{\rm S}$ ist gleich der ungünstigsten Fehlerwahrscheinlichkeit $p_{\rm U} = \underline {10^{\rm -6}}$. Die untere Schranke liegt bei $\underline {0.25 \cdot 10^{\rm -6}}$, ist also um den Faktor 4 kleiner.