Aufgabe 1.4Z: Zum Dopplereffekt

• Zurück zum Buch

Zur Berechnung von Dopplerfrequenzen

Als „Dopplereffekt” bezeichnet man die Veränderung der wahrgenommenen Frequenz von Wellen jeder Art, während sich Quelle (Sender) und Beobachter (Empfänger) relativ zueinander bewegen.

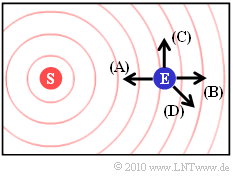
Wir gehen stets von einem festen Sender aus, während sich der Empfänger in vier verschiedene Richtungen (A), (B), (C) und (D) bewegen kann (siehe Grafik).

Untersucht werden sollen verschiedene Geschwindigkeiten:

• eine unrealistisch große Geschwindigkeit $\upsilon_1 = 0.6 \cdot c = 1.8 \cdot 10^8 \ {\rm m/s}$,
• die Maximalgeschwindigkeit $\upsilon_2 = 3 \ {\rm km/s} \ (10800 \ {\rm km/h})$ bei unbemanntem Testflug,
• etwa die Höchstgeschwindigkeit $\upsilon_3 = 30 \ {\rm m/s} = 108 \ \rm km/h$ auf Bundesstraßen.

Die im Theorieteil angegebenen Gleichungen für die Empfangsfrequenz lauten

• unter Berücksichtigung der Relativitätstheorie (kurz als „relativistisch” bezeichnet

$${\rm Gleichung \hspace{0.15cm}(1):}\hspace{0.2cm}f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2}}{1 - v/c \cdot \cos(\alpha)} \hspace{0.05cm},$$

• ohne Berücksichtigung relativistischer Eigenschaften (kurz „herkömmlich”):

$${\rm Gleichung \hspace{0.15cm}(2):}\hspace{0.2cm}f_{\rm E} = f_{\rm S} \cdot \left [ 1 + {v}/{c} \cdot \cos(\alpha) \right ] \hspace{0.05cm}.$$

Hinweis:

• Die Aufgabe gehört zu Kapitel Statistische Bindungen innerhalb des Rayleigh–Prozesses.
• $c = 3 \cdot 10^8 \ \rm m/s$ nennt man Lichtgeschwindigkeit.
• Zur Überprüfung Ihrer Ergebnisse können Sie folgendes Interaktionsmodul benutzen: Zur Verdeutlichung des Dopplereffekts

Fragebogen

1

Welche Dopplerfrequenzen ergeben sich für die Geschwindigkeiten $\upsilon_1$ und $\upsilon_2$ in Fahrtrichtung (A) mit der relativistischen Gleichung (1)?

${\rm Richtung \ (A)}, \upsilon_1 : f_{\rm D}/f_{\rm S}$ = $\ 10^0$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \upsilon_2 : f_{\rm D}/f_{\rm S}$ = $\ 10^{\rm –5}$

2

Welche Dopplerfrequenzen erhält man bei sonst gleichen Bedingungen für die entgegengesetzte Fahrtrichtung (B)? Hinweis: Gleichung (1).

${\rm Richtung \ (B)}, \upsilon_1 : f_{\rm D}/f_{\rm S}$ = $\ 10^0$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \upsilon_2 : f_{\rm D}/f_{\rm S}$ = $\ 10^{\rm –5}$

3

Welche Ergebnisse erhält man bei ansonsten gleichen Bedingungen mit der herkömmlichen Dopplergleichung (2)?

${\rm Richtung \ (A)}, \upsilon_1 : f_{\rm D}/f_{\rm S}$ = $\ 10^0$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \upsilon_2 : f_{\rm D}/f_{\rm S}$ = $\ 10^{\rm –5}$

${\rm Richtung \ (B)}, \upsilon_1 : f_{\rm D}/f_{\rm S}$ = $\ 10^0$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \upsilon_2 : f_{\rm D}/f_{\rm S}$ = $\ 10^{\rm –5}$

4

Welche Dopplerfrequenzen ergeben sich für die Richtungen (C) und (D)? Hinweis: Gleichung (2), Geschwindigkeit $\upsilon_3$, Sendefrequenz $f_{\rm S} = 2 \ \rm GHz$.

${\rm Richtung \ (C)}, \upsilon_3 : f_{\rm D}/f_{\rm S}$ = $\ 10^0$

${\rm Richtung \ (D)}, \upsilon_3 : f_{\rm D}/f_{\rm S}$ = $\ 10^0$

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)