Aufgabe 1.4Z: Zum Dopplereffekt
Als „Dopplereffekt” bezeichnet man die Veränderung der wahrgenommenen Frequenz von Wellen jeder Art, während sich Quelle (Sender) und Beobachter (Empfänger) relativ zueinander bewegen.
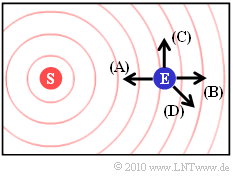
Wir gehen stets von einem festen Sender aus, während sich der Empfänger in vier verschiedene Richtungen (A), (B), (C) und (D) bewegen kann (siehe Grafik).
Untersucht werden sollen verschiedene Geschwindigkeiten:
- eine unrealistisch große Geschwindigkeit $\upsilon_1 = 0.6 \cdot c = 1.8 \cdot 10^8 \ {\rm m/s}$,
- die Maximalgeschwindigkeit $\upsilon_2 = 3 \ {\rm km/s} \ (10800 \ {\rm km/h})$ bei unbemanntem Testflug,
- etwa die Höchstgeschwindigkeit $\upsilon_3 = 30 \ {\rm m/s} = 108 \ \rm km/h$ auf Bundesstraßen.
Die im Theorieteil angegebenen Gleichungen für die Empfangsfrequenz lauten
- unter Berücksichtigung der Relativitätstheorie (kurz als „relativistisch” bezeichnet
- $${\rm Gleichung \hspace{0.15cm}(1):}\hspace{0.2cm}f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2}}{1 - v/c \cdot \cos(\alpha)} \hspace{0.05cm},$$
- ohne Berücksichtigung relativistischer Eigenschaften (kurz „herkömmlich”):
- $${\rm Gleichung \hspace{0.15cm}(2):}\hspace{0.2cm}f_{\rm E} = f_{\rm S} \cdot \left [ 1 + {v}/{c} \cdot \cos(\alpha) \right ] \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Themengebiet von Statistische Bindungen innerhalb des Rayleigh–Prozesses.
- Zur Überprüfung Ihrer Ergebnisse können Sie das Interaktionsmodul WDF, VTF und Momente benutzen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Hinweis:
- Die Aufgabe gehört zu Kapitel Statistische Bindungen innerhalb des Rayleigh–Prozesses.
- $c = 3 \cdot 10^8 \ \rm m/s$ nennt man Lichtgeschwindigkeit.
- Zur Überprüfung Ihrer Ergebnisse können Sie folgendes Interaktionsmodul benutzen: Zur Verdeutlichung des Dopplereffekts
Fragebogen
Musterlösung
- $$f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2}}{1 - v/c } \hspace{0.3cm} \Rightarrow \hspace{0.3cm} f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm S} \cdot \left [ \frac{\sqrt{1 - (v/c)^2}}{1 - v/c } - 1 \right ]$$
- $$\Rightarrow \hspace{0.3cm}\frac{f_{\rm D}}{f_{\rm S}} = \frac{\sqrt{1 - (v/c)^2}}{1 - v/c } - 1 \hspace{0.05cm}.$$
Man $\upsilon_1/c = 0.6$ erhält man:
- $$\frac{f_{\rm D}}{f_{\rm S}} = \frac{\sqrt{1 - 0.6^2}}{1 - 0.6 } - 1 = \frac{0.8}{0.4 } - 1 \hspace{0.15cm} \underline{ = 1} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {f_{\rm E}}/{f_{\rm S}} = 2 \hspace{0.05cm}.$$
Entsprechend gilt mit $\upsilon_2/c = 10^{\rm –5}$:
- $$\frac{f_{\rm D}}{f_{\rm S}} = \frac{\sqrt{1 - (10^{-5})^2}}{1 - (10^{-5}) } - 1 \approx 1 + 10^{-5} - 1 \hspace{0.15cm} \underline{ = 10^{-5}} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {f_{\rm E}}/{f_{\rm S}} = 1.00001 \hspace{0.05cm}.$$
(2) Nun entfernt sich der Empfänger vom Sender ($\alpha = 180^°$). Die Empfangsfrequenz $f_{\rm E}$ ist kleiner als die Sendefrequenz $f_{\rm S}$ und die Dopplerfrequenz $f_{\rm D}$ negativ. Mit ${\rm cos}(\alpha) = \ –1$ erhält man nun:
- $$\frac{f_{\rm D}}{f_{\rm S}} = \frac{\sqrt{1 - (v/c)^2}}{1 + v/c } - 1 = \left\{ \begin{array}{c} \hspace{0.15cm} \underline{ -0.5} \\ \\ \hspace{0.15cm} \underline{ -10^{-5}} \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.2cm}{\rm f\ddot{u}r}\hspace{0.15cm} v_1/c = 0.6 \\ \\ {\rm f\ddot{u}r}\hspace{0.15cm} v_2/c = 10^{-5} \\ \end{array} \hspace{0.05cm}.$$
Umgerechnet auf $f_{\rm E}/f_{\rm S}$ ergibt sich:
- $$\frac{f_{\rm E}}{f_{\rm S}} = \left\{ \begin{array}{c} \hspace{0.15cm} { 0.5} \\ \\ \hspace{0.15cm} { 0.99999} \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.2cm}{\rm f\ddot{u}r}\hspace{0.15cm} v_1/c = 0.6 \\ \\ {\rm f\ddot{u}r}\hspace{0.15cm} v_2/c = 10^{-5} \\ \end{array} \hspace{0.05cm}.$$
(3) Hier gelten folgende Gleichungen:
- $$f_{\rm E} = f_{\rm S} \cdot \left [ 1 + \frac{v}{c} \cdot \cos(\alpha) \right ] \Rightarrow \hspace{0.3cm}\frac{f_{\rm D}}{f_{\rm S}} = \frac{v}{c} \cdot \cos(\alpha) \hspace{0.05cm}.$$
Daraus ergeben sich folgende Zahlenwerte:
- Richtung (A), $\upsilon_1 /c = 1.8 \cdot 10^8 \ {\rm m/s}: f_{\rm D}/f_{\rm S} \ \underline {= \ 0.6} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 1.6,$
- Richtung (A), $\upsilon_2 /c = 3.0 \cdot 10^3 \ {\rm m/s}: f_{\rm D}/f_{\rm S} \ \underline {= \ 10^{\rm –5}} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 1.00001,$
- Richtung (B), $\upsilon_1 /c = 1.8 \cdot 10^8 \ {\rm m/s}: f_{\rm D}/f_{\rm S} \ \underline {= \ –0.6} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 0.4,$
- Richtung (B), $\upsilon_2 /c = 3.0 \cdot 10^3 \ {\rm m/s}: f_{\rm D}/f_{\rm S} \ \underline {= \ –10^{\rm –5}} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 0.99999.$
Man erkennt, dass für realistische Geschwindigkeiten – dazu rechnen wir auch $\upsilon \ \approx \ 10000 \ {\rm km/h}$ – die herkömmliche Gleichung (2) bis hin zur Genauigkeit eines Taschenrechners das gleiche Ergebnis liefert wie die relativistische Gleichung (1). Mit der Näherung liefern die Winkel $\alpha = 0^°$ und $\alpha = 180^°$ den gleichen Betrag der Dopplerfrequenz. Die Näherungen unterscheiden sich nur im Vorzeichen. Bei der relativistischen Gleichung ist diese Symmetrie nicht mehr gegeben (siehe Teilaufgaben 1) und 2)).
(4) Gleichung (2) führt hier zum Ergebnis:
- $$f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm S} \cdot \frac{v_3}{c} \cdot \cos(\alpha) \hspace{0.05cm}.$$
- Die Fahrtrichtung (C) verläuft senkrecht ($\alpha = 90^°$) zur Verbindungslinie Sender–Empfänger. In diesem Fall tritt keine Dopplerverschiebung auf: $f_{\rm D} \ \underline {= \ 0}$.
- Die Bewegungsrichtung (D) ist durch $\alpha = \ –135°$ charakterisiert. Daraus resultiert:
- $$f_{\rm D} = 2 \cdot 10^{9}\,\,{\rm Hz} \cdot \frac{30\,\,{\rm m/s}}{3 \cdot 10^{8}\,\,{\rm m/s}} \cdot \cos(-135^{\circ}) \hspace{0.15cm} \underline{ \approx -141\,\,{\rm Hz}} \hspace{0.05cm}.$$